公平組合遊戲-巴什遊戲、尼姆遊戲和SG函數
文章目錄
公平組合遊戲
公平組合遊戲(Impartral Combinatorial Game)是滿足以下特徵的一類問題:
- 有兩個玩家,遊戲規則對兩人是公平的
- 兩人輪流交替回合,當一個玩家不能走時遊戲結束
- 遊戲狀態和能走的步數都是有限的
- 遊戲局勢不能用來區分玩家身份(比如圍棋有黑白方就不屬於)
- P點(P-position)是指前一個玩家(即剛走過一步的玩家)的必勝位置,表示先手必敗
- N點(N-position)是指下一個玩家的必勝位置,表示先手必勝
巴什遊戲
巴什遊戲(Bash Game)是
n
n
n顆石子,每次可以拿1~
m
m
m顆,兩人輪流。
結論是若
n
n
n%
(
m
+
1
)
=
=
0
(m+1)==0
(m+1)==0則先手敗,否則先手勝。
HDU-1846
Problem Description
不重要的背景。。。
各位勇敢者要玩的第一個遊戲是什麼呢?很簡單,它是這樣定義的:
1、 本遊戲是一個二人遊戲;
2、 有一堆石子一共有n個;
3、 兩人輪流進行;
4、 每走一步可以取走1…m個石子;
5、 最先取光石子的一方為勝;
如果遊戲的雙方使用的都是最優策略,請輸出哪個人能贏。
Input
輸入資料首先包含一個正整數C(C<=100),表示有C組測試資料。
每組測試資料佔一行,包含兩個整數n和m(1<=n,m<=1000),n和m的含義見題目描述。
Output
如果先走的人能贏,請輸出「first」,否則請輸出「second」,每個範例的輸出佔一行。
Sample Input
2
23 2
4 3
Sample Output
first
second
#include<bits/stdc++.h>
using namespace std;
int t, n, m;
int main() {
scanf("%d", &t);
while(t--) {
scanf("%d%d", &n, &m);
if (n % (m + 1) == 0)
puts("second");
else puts("first");
}
return 0;
}
尼姆遊戲
尼姆遊戲(Nim Game)是由
n
n
n對石子,數量分別是{a1,a2,…,an},兩個玩家輪流拿石子,每次可以從任意一堆拿走任意數量的石子,拿到最後一個石子的玩家獲勝。
結論是若a1⊕a2⊕…an≠0,則先手必勝(N),否則先手必敗(P)
HDU-1850
HDU-1850 Being a Good Boy in Spring Festival
Problem Description
不重要的背景。。。
咱們玩個小遊戲吧 ACM課上學的呢~
下面是一個二人小遊戲:桌子上有M堆撲克牌;每堆牌的數量分別為Ni(i=1…M);兩人輪流進行;每走一步可以任意選擇一堆並取走其中的任意張牌;桌子上的撲克全部取光,則遊戲結束;最後一次取牌的人為勝者。
現在我們不想研究到底先手為勝還是為負,我只想問大家:
——「先手的人如果想贏,第一步有幾種選擇呢?」
Input
輸入資料包含多個測試用例,每個測試用例佔2行,首先一行包含一個整數M(1<M<=100),表示撲克牌的堆數,緊接著一行包含M個整數Ni(1<=Ni<=1000000,i=1…M),分別表示M堆撲克的數量。M為0則表示輸入資料的結束。
Output
如果先手的人能贏,請輸出他第一步可行的方案數,否則請輸出0,每個範例的輸出佔一行。
Sample Input
3
5 7 9
0
Sample Output
1
分析:
設
H
H
H是出來
a
[
i
]
a[i]
a[i]外的其他所有數的互斥或,則
a
n
s
=
H
ans=H
ans=H^
a
[
i
]
a[i]
a[i]
a
n
s
ans
ans^
a
[
i
]
=
H
a[i]=H
a[i]=H ^
a
[
i
]
a[i]
a[i] ^
a
[
i
]
=
H
a[i]=H
a[i]=H
所以
(
a
n
s
(ans
(ans^
a
[
i
]
)
<
=
a
[
i
]
a[i])<=a[i]
a[i])<=a[i],即
H
<
=
a
[
i
]
H<=a[i]
H<=a[i],可以把
a
[
i
]
a[i]
a[i]減少到
H
H
H,就是一種可行方案。
實在不行這邊建議打表
#include<bits/stdc++.h>
using namespace std;
const int maxn = 102;
int m, ans, sum, a[maxn];
int main() {
while (~scanf("%d", &m) && m) {
ans = sum = 0;
for (int i = 0; i < m; i++) {
scanf("%d", &a[i]);
ans ^= a[i];
}
if (ans == 0)puts("0");
else {
for (int i = 0; i < m; i++) {
if ((ans ^ a[i]) <= a[i])
sum++;
}
printf("%d\n", sum);
}
}
return 0;
}
HDU-1907
Problem Description
Little John is playing very funny game with his younger brother. There is one big box filled with M&Ms of different colors. At first John has to eat several M&Ms of the same color. Then his opponent has to make a turn. And so on. Please note that each player has to eat at least one M&M during his turn. If John (or his brother) will eat the last M&M from the box he will be considered as a looser and he will have to buy a new candy box.
Both of players are using optimal game strategy. John starts first always. You will be given information about M&Ms and your task is to determine a winner of such a beautiful game.
Input
The first line of input will contain a single integer T – the number of test cases. Next T pairs of lines will describe tests in a following format. The first line of each test will contain an integer N – the amount of different M&M colors in a box. Next line will contain N integers Ai, separated by spaces – amount of M&Ms of i-th color.
Constraints:
1 <= T <= 474,
1 <= N <= 47,
1 <= Ai <= 4747
Output
Output T lines each of them containing information about game winner. Print 「John」 if John will win the game or 「Brother」 in other case.
Sample Input
2
3
3 5 1
1
1
Sample Output
John
Brother
分析:
這道題反過來了,拿最後一顆石子則輸,反尼姆博弈,注意特殊情況處理下即可。
特殊情況: 若所有石堆的數量都是1,那麼判斷奇偶即可(即互斥或結果等於0先手必勝)。
否則互斥或結果不等於0則先手必勝。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 102;
int t, n, ans, a;
int main() {
scanf("%d", &t);
while (t--) {
bool tag = false;
ans = 0;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &a);
ans ^= a;
if (a > 1)tag = true;
}
if (tag && ans != 0) //全1且互斥或非0
puts("John");
else if (!tag && ans == 0) //否則互斥或為0也是先手必勝
puts("John");
else puts("Brother");
}
return 0;
}
SG函數
SG函數(Sprague-Grundy)函數是在一個圖
G
(
X
,
F
)
G(X,F)
G(X,F)中,定義結點
x
x
x的sg函數為
s
g
(
x
)
sg(x)
sg(x),它等於沒有指定給它的任意後繼結點的
s
g
sg
sg值的最小非負整數。
有點拗口,不急,他就是找一個不屬於集合裡的最小非負整數,這個集合就是圖的後記結點。
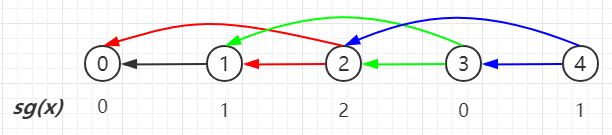
- sg(0)=0,因為結點0沒有後繼結點,0是最小非負整數
- sg(1)=1,結點1後繼結點是0,不等於sg(0)的最小非負整數是1
- sg(2)=2,其後繼節點是0和1,不等於sg(0)、sg(1)的最小非負整數是2
- sg(3)=0,其後繼節點是1和2,不等於sg(1)、sg(2)的最小非負整數是0
- sg(4)=1,其後繼節點是2和3,不等於sg(2)、sg(3)的最小非負整數是1
SG函數求解巴什遊戲
結論:
s
g
(
x
)
=
0
sg(x)=0
sg(x)=0的結點
x
x
x是先手必敗點,也就是P點。
證明
- 根據sg函數性質,sg(x)=0的結點,沒有sg值等於0的後繼節點;sg(y)>0的任意結點,必有一條邊通向sg值為0的某個後記結點;
- 若sg(x)=0的結點時圖上的終點(沒有後繼節點,出度為0),顯示x=0,它是一個P點;若x有後繼節點,那麼這些後繼結點都能通向某個sg值為0的結點。當玩家甲處於sg(x)=0的結點時,只能轉移到sg(x)≠0的結點,下一個玩家乙必然轉移到sg(x)=0的點,從而讓甲不利,所以sg(x)=0的點是先手必敗點。
HDU-1846
HDU-1846 Brave Game
題目詳情同上文
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1003;
int t, n, m, sg[maxn], s[maxn];
void getsg() {
for (int i = 1; i <= n; i++) {
memset(s, 0, sizeof(s));
for (int j = 1; j <= m && j <= i; j++)
s[sg[i - j]] = 1; //更新後繼結點
for (int j = 0; j <= n; j++) //找最小非負整數
if (!s[j]) {
sg[i] = j;
break;
}
}
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d%d", &n, &m);
getsg();
if (sg[n])puts("first");
else puts("second");
}
return 0;
}
(
插播反爬資訊)博主CSDN地址:https://blog.csdn.net/qq_45034708
SG函數求解尼姆遊戲
結論:
計算每堆石子的sg值,把所有sg值互斥或,若結果=0則先手必敗。
HDU-1848
HDU-1846 Fibonacci again and again
Problem Description
不重要的背景。。。
今天,又一個關於Fibonacci的題目出現了,它是一個小遊戲,定義如下:
1、 這是一個二人遊戲;
2、 一共有3堆石子,數量分別是m, n, p個;
3、 兩人輪流走;
4、 每走一步可以選擇任意一堆石子,然後取走f個;
5、 f只能是菲波那契數列中的元素(即每次只能取1,2,3,5,8…等數量);
6、 最先取光所有石子的人為勝者;
假設雙方都使用最優策略,請判斷先手的人會贏還是後手的人會贏。
Input
輸入資料包含多個測試用例,每個測試用例佔一行,包含3個整數m,n,p(1<=m,n,p<=1000)。
m=n=p=0則表示輸入結束。
Output
如果先手的人能贏,請輸出「Fibo」,否則請輸出「Nacci」,每個範例的輸出佔一行。
Sample Input
1 1 1
1 4 1
0 0 0
Sample Output
Fibo
Nacci
分析:
注意處理下後繼節點即可,值只能取斐波那契數列,然後套結論。(該題三堆石子,多堆也一樣)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1003;
int sg[maxn], s[maxn];
int n, m, p;
int fibo[15] = { 1,2,3 };
void getsg() {
for (int i = 0; i <= maxn; i++) {
memset(s, 0, sizeof(s));
for (int j = 0; j < 15 && fibo[j] <= i; j++)
s[sg[i - fibo[j]]] = 1; //更新後繼節點
for (int j = 0; j <= maxn; j++) //找最小非負整數
if (!s[j]) {
sg[i] = j;
break;
}
}
}
int main() {
for (int i = 3; i < 15; i++)
fibo[i] = fibo[i - 1] + fibo[i - 2];
getsg();
while (~scanf("%d%d%d", &n, &m, &p) && (n + m + p)) {
if (sg[n] ^ sg[m] ^ sg[p])
puts("Fibo");
else puts("Nacci");
}
return 0;
}
HDU-2999
HDU-2999 Stone Game, Why are you always there?
Problem Description
「Alice and Bob are playing stone game…」
「Err… Feel bored about the stone game? Don’t be so, because stone game changes all the time!」
「What the hell are they thinking for?」
「You know, whenever Alice is trying to make fun of Bob, she asked him to play stone game with him.」
「Poor Bob… What’s the rule today?」
「It seems Alice only allows some fixed numbers of continuous stones can be taken each time. And they begin with one string of stones.」
「A string? Formed as a circle or a line?」
「A line.」
「Well, I think I may help Bob with that.」
「How?」
「I may tell him to skip this round if he has no chance to win.」
「Good idea maybe, I mean, Alice always let Bob play first, because she think herself is smart enough to beat Bob no matter how.」
「Yes, she’s actually right about herself. Let me see if Bob has a chance to win…」
…
Input
There are multiple test cases, for each test case:
The first line has a positive integer N (1<=N<=100).
The second line contains N positive integers, a1, a2 … an, separated by spaces, which indicate the fixed numbers Alice gives.
The third line, a positive integer M. (M<=1000)
Following M lines, one positive integer K (K<=1000) each line. K means in this round, the length of the stone string.
Output
For each K, output 「1」 if Bob has a chance to win, output 「2」 if Bob has no chance, or 「0」 if it’s undeterminable.
Sample Input
3
1 5 1
1
1
Sample Output
1
分析:
取出連續的石子,注意位置不能合併(2拿完後,1和3認為是不相鄰的),比如5個石子,S={2},拿完後剩(3,4,5)、{(1),(4,5)}、{(1,2),(5)}和(1,2,3)四種情況,只關心剩餘區間的長度即{0,3}、{1,2},後繼狀態變成了兩個子區間長度的SG函數的互斥或和。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1003;
int sg[maxn], s[maxn];
int n, m, k, a[102];
void getsg() {
for (int i = 0; i <= maxn; i++) {
memset(s, 0, sizeof(s));
for (int j = 0; j < n && a[j] <= i; j++)
for (int k = i - a[j]; k >= 0; k--)//兩個狀態互斥或
s[sg[k] ^ sg[i - a[j] - k]] = 1;
for (int j = 0; j <= maxn; j++)
if (!s[j]) {
sg[i] = j;
break;
}
}
}
int main() {
while (~scanf("%d", &n)) {
for (int i = 0; i < n; i++)
scanf("%d", &a[i]);
sort(a, a + n);
getsg();
scanf("%d", &m);
while (m--) {
scanf("%d", &k);
if (sg[k])puts("1");
else puts("2");
}
}
return 0;
}
HDU-1524
Problem Description
Let’s design a new chess game. There are N positions to hold M chesses in this game. Multiple chesses can be located in the same position. The positions are constituted as a topological graph, i.e. there are directed edges connecting some positions, and no cycle exists. Two players you and I move chesses alternately. In each turn the player should move only one chess from the current position to one of its out-positions along an edge. The game does not end, until one of the players cannot move chess any more. If you cannot move any chess in your turn, you lose. Otherwise, if the misfortune falls on me… I will disturb the chesses and play it again.
Do you want to challenge me? Just write your program to show your qualification!
Input
Input contains multiple test cases. Each test case starts with a number N (1 <= N <= 1000) in one line. Then the following N lines describe the out-positions of each position. Each line starts with an integer Xi that is the number of out-positions for the position i. Then Xi integers following specify the out-positions. Positions are indexed from 0 to N-1. Then multiple queries follow. Each query occupies only one line. The line starts with a number M (1 <= M <= 10), and then come M integers, which are the initial positions of chesses. A line with number 0 ends the test case.
Output
There is one line for each query, which contains a string 「WIN」 or 「LOSE」. 「WIN」 means that the player taking the first turn can win the game according to a clever strategy; otherwise 「LOSE」 should be printed.
Sample Input
4
2 1 2
0
1 3
0
1 0
2 0 2
0
4
1 1
1 2
0
0
2 0 1
2 1 1
3 0 1 3
0
Sample Output
WIN
WIN
WIN
LOSE
WIN
分析:
有向無環圖,最後不能移動就輸了,就是sg函數的定義,用dfs互斥或路徑即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1003;
int sg[maxn], s[maxn];
int n, m, k, mp[maxn][maxn];
int dfs(int x) {
if (sg[x] != -1)return sg[x];
int vis[maxn] = { 0 };
for (int i = 0; i < n; i++)
if (mp[x][i])
vis[dfs(i)] = 1;
for (int i = 0; i < maxn; i++) {
if (!vis[i]) {
sg[x] = i;
break;
}
}
return sg[x];
}
int main() {
while (~scanf("%d", &n)) {
memset(sg, -1, sizeof(sg));
memset(mp, 0, sizeof(mp));
for (int i = 0; i < n; i++) {
scanf("%d", &m);
for (int j = 0; j < m; j++) {
scanf("%d", &k);
mp[i][k] = 1;
}
if (m == 0)sg[i] = 0;
}
while (~scanf("%d", &m) && m) {
int ans = 0;
for (int i = 0; i < m; i++) {
scanf("%d", &k);
if (sg[k] != -1)ans ^= sg[k];
else ans ^= dfs(k);
}
if (ans)puts("WIN");
else puts("LOSE");
}
}
return 0;
}
原創不易,請勿轉載(
本不富裕的存取量雪上加霜)
博主首頁:https://blog.csdn.net/qq_45034708
如果文章對你有幫助,記得一鍵三連❤