機器學習(西瓜書)之二項檢驗的理解
前言
二項檢驗在周志華老師的西瓜書中並沒有做太多解釋,自己也是網上搜尋了相關的資料和其他人的看法,並結合了自己的一些理解寫下部落格記錄一下。
內容引出
我們在對學習器的效能進行評估比較的時候,有了評估方法和效能度量也不一定能很好判斷學習器的優劣,通常是用統計假設檢驗,基於假設檢驗的結果我們可以推斷出,若在測試集上觀察到學習器A比B好,則A的泛化效能是否在統計意義上優於B,以及這個結論的把握有多大。這裡,預設以錯誤率為效能度量,用 ϵ \epsilon ϵ表示,即泛化錯誤率。
假設檢驗中的「假設」是對學習器泛化錯誤率分佈的某種判斷或者是猜想,比如「 ϵ = ϵ 0 \epsilon=\epsilon_{0} ϵ=ϵ0」。現實的任務中我們不知道學習器的泛化錯誤率,只能獲知其測試錯誤率 ϵ ^ \hat{\epsilon} ϵ^,而且泛化錯誤率和測試錯誤率不一定相同,直觀上,它們兩者接近的可能性比較大,相差很遠的可能性比較小。由此我們可以根據測試錯誤率估推出泛化錯誤率的分佈。這也是此章節的目的。
二項檢驗
泛化錯誤率為 ϵ \epsilon ϵ的學習器在一個樣本上犯錯的概率是 ϵ \epsilon ϵ,而測試錯誤率 ϵ ^ \hat{\epsilon} ϵ^表示的是在m個測試樣本中恰好有 ϵ ^ ∗ m \hat{\epsilon}*m ϵ^∗m個被誤分類。我們假定測試樣本是從總體分佈中獨立取樣得到的,那請問泛化錯誤率為 ϵ \epsilon ϵ的學習中將m0個樣本誤分類,其餘樣本全部分類正確的概率是多少?
如果上面的看不懂沒關係,我們來分析一下這個問題,假如你去投籃,你不能投中的概率是 ϵ \epsilon ϵ,你總共只能投m個,其中m0個投不中的概率是多少?這個問題我們都不陌生吧,因為你每次投籃都是相互獨立的,所以我們可以用二項分佈的方法迅速得出結果 ( m m 0 ) ∗ ϵ m 0 ∗ ( 1 − ϵ ) m − m 0 \begin{pmatrix} m \\ m_0 \end{pmatrix}*\epsilon^{m_0}*(1-\epsilon)^{m-m_0} (mm0)∗ϵm0∗(1−ϵ)m−m0這個公式的前面的矩陣的意思其實就是排列組合,相當於C(m,m0)。那對之前的問題也是一樣的道理,它也滿足二項分佈,所以結果也是一樣 ( m m 0 ) ∗ ϵ m 0 ∗ ( 1 − ϵ ) m − m 0 \begin{pmatrix} m \\ m_0 \end{pmatrix}*\epsilon^{m_0}*(1-\epsilon)^{m-m_0} (mm0)∗ϵm0∗(1−ϵ)m−m0所以由此我們可以估算出恰好將 ϵ ^ ∗ m \hat{\epsilon}*m ϵ^∗m個樣本誤分類的概率,這也表達了在包含m個樣本的測試集上,泛化錯誤率為 ϵ \epsilon ϵ的學習器被測得測試錯誤率為 ϵ ^ \hat{\epsilon} ϵ^的概率: P ( ϵ ^ ; ϵ ) = ( m m ∗ ϵ ^ ) ∗ ϵ m ∗ ϵ ^ ∗ ( 1 − ϵ ) m − m ∗ ϵ ^ P(\hat{\epsilon};\epsilon)=\begin{pmatrix} m \\ m*\hat{\epsilon} \end{pmatrix}*\epsilon^{m*\hat{\epsilon}}*(1-\epsilon)^{m-m*\hat{\epsilon}} P(ϵ^;ϵ)=(mm∗ϵ^)∗ϵm∗ϵ^∗(1−ϵ)m−m∗ϵ^書上給出的公式其實是很好理解的,但是其最後直接得出結論概率在 ϵ = ϵ ^ \epsilon=\hat{\epsilon} ϵ=ϵ^時最大,其中略過求解過程,所以這裡對其進行推導。
這裡其實用到的時極大似然法(不太懂的同學可以看看這篇部落格極大似然估計)我們先對原式進行求對數
l
n
(
P
(
ϵ
^
;
ϵ
)
)
=
l
n
(
(
m
m
∗
ϵ
^
)
∗
ϵ
m
∗
ϵ
^
∗
(
1
−
ϵ
)
m
−
m
∗
ϵ
^
)
ln(P(\hat{\epsilon};\epsilon))=ln(\begin{pmatrix} m \\ m*\hat{\epsilon} \end{pmatrix}*\epsilon^{m*\hat{\epsilon}}*(1-\epsilon)^{m-m*\hat{\epsilon}})
ln(P(ϵ^;ϵ))=ln((mm∗ϵ^)∗ϵm∗ϵ^∗(1−ϵ)m−m∗ϵ^)這裡要提一個關於對數函數的性質
l
n
(
a
∗
b
)
=
l
n
(
a
)
+
l
n
(
b
)
ln(a*b)=ln(a)+ln(b)
ln(a∗b)=ln(a)+ln(b)所以根據這個性質我們可以對原式進行分解
l
n
(
P
(
ϵ
^
;
ϵ
)
)
=
l
n
(
(
m
m
∗
ϵ
^
)
∗
ϵ
m
∗
ϵ
^
∗
(
1
−
ϵ
)
m
−
m
∗
ϵ
^
)
=
l
n
(
(
m
m
∗
ϵ
^
)
)
+
l
n
(
ϵ
m
∗
ϵ
^
)
+
l
n
(
(
1
−
ϵ
)
m
−
m
∗
ϵ
^
)
=
l
n
(
(
m
m
∗
ϵ
^
)
)
+
(
m
∗
ϵ
^
)
∗
l
n
(
ϵ
)
+
(
m
−
m
∗
ϵ
^
)
l
n
(
(
1
−
ϵ
)
)
ln(P(\hat{\epsilon};\epsilon))=ln(\begin{pmatrix} m \\ m*\hat{\epsilon} \end{pmatrix}*\epsilon^{m*\hat{\epsilon}}*(1-\epsilon)^{m-m*\hat{\epsilon}})\\=ln(\begin{pmatrix} m \\ m*\hat{\epsilon} \end{pmatrix})+ln(\epsilon^{m*\hat{\epsilon}})+ln((1-\epsilon)^{m-m*\hat{\epsilon}})\\=ln(\begin{pmatrix} m \\ m*\hat{\epsilon} \end{pmatrix})+({m*\hat{\epsilon}})*ln(\epsilon)+({m-m*\hat{\epsilon}})ln((1-\epsilon))
ln(P(ϵ^;ϵ))=ln((mm∗ϵ^)∗ϵm∗ϵ^∗(1−ϵ)m−m∗ϵ^)=ln((mm∗ϵ^))+ln(ϵm∗ϵ^)+ln((1−ϵ)m−m∗ϵ^)=ln((mm∗ϵ^))+(m∗ϵ^)∗ln(ϵ)+(m−m∗ϵ^)ln((1−ϵ))然後我們再對式子進行求導,現在對
ϵ
\epsilon
ϵ求導,此時要比之前更容易求導
∂
(
l
n
(
P
(
ϵ
^
;
ϵ
)
)
)
∂
ϵ
=
∂
(
l
n
(
(
m
m
∗
ϵ
^
)
)
)
+
∂
(
(
m
∗
ϵ
^
)
∗
l
n
(
ϵ
)
)
+
∂
(
(
m
−
m
∗
ϵ
^
)
l
n
(
(
1
−
ϵ
)
)
)
=
0
+
(
m
∗
ϵ
^
)
∗
1
ϵ
+
(
m
∗
ϵ
^
−
m
)
∗
1
1
−
ϵ
=
m
∗
(
ϵ
^
−
ϵ
)
(
1
−
ϵ
)
∗
ϵ
\frac{\partial(ln(P(\hat{\epsilon};\epsilon)))}{\partial\epsilon}=\partial(ln(\begin{pmatrix} m \\ m*\hat{\epsilon} \end{pmatrix}))+\partial(({m*\hat{\epsilon}})*ln(\epsilon))+\partial(({m-m*\hat{\epsilon}})ln((1-\epsilon)))\\=0+({m*\hat{\epsilon}})*\frac{1}{\epsilon}+({m*\hat{\epsilon}-m})*\frac{1}{1-\epsilon}\\=\frac{m*(\hat{\epsilon}-\epsilon)}{(1-\epsilon)*\epsilon}
∂ϵ∂(ln(P(ϵ^;ϵ)))=∂(ln((mm∗ϵ^)))+∂((m∗ϵ^)∗ln(ϵ))+∂((m−m∗ϵ^)ln((1−ϵ)))=0+(m∗ϵ^)∗ϵ1+(m∗ϵ^−m)∗1−ϵ1=(1−ϵ)∗ϵm∗(ϵ^−ϵ)
我們也知道當其導數為0時有最大值,且此時
ϵ
=
ϵ
^
\epsilon=\hat{\epsilon}
ϵ=ϵ^。根據書上的例子,
ϵ
=
0.3
\epsilon=0.3
ϵ=0.3,m=10,我們可以用Python程式碼將其表示出來:
import matplotlib.pyplot as plt
from scipy.special import comb
from matplotlib.font_manager import FontProperties
import numpy as np
import matplotlib
a = 0.3
m = 10
p = []
for error in range(11):
k = comb(m,error)*(a**error)*((1-a)**(m-error))
p.append(k)
fig = plt.figure()
ax = fig.add_subplot(111)
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
plt.xlabel('誤分類樣本數',fontproperties=font)
plt.ylabel('概率',fontproperties=font)
y = np.arange(0,0.35,0.05)
x = np.arange(0,11.0,1.0)
plt.xticks(x)
plt.yticks(y)
ax.scatter(x,p)
plt.plot(x,p)
plt.show()
我們可以得到和書上基本一致的影象
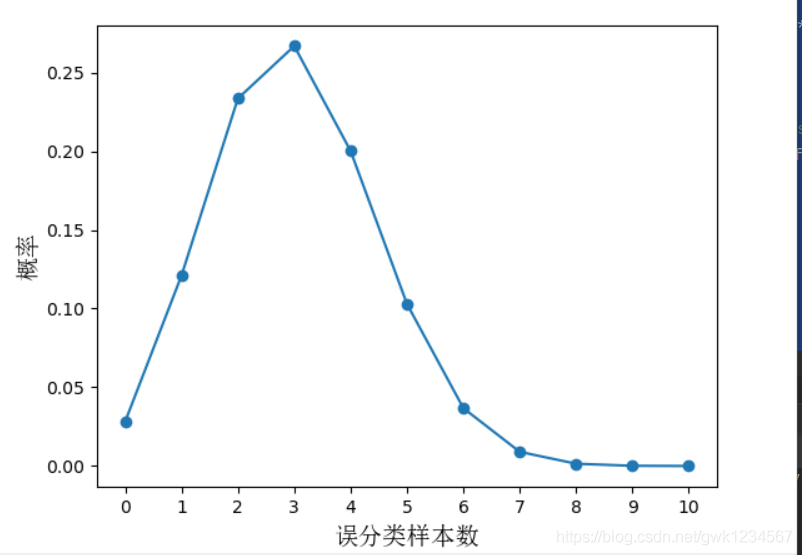
圖中的橫座標雖然是誤分類的樣本數,但是除以樣本總數即可得到此時的測試錯誤率
ϵ
^
\hat{\epsilon}
ϵ^,由圖我們也可以看出當泛化錯誤率
ϵ
\epsilon
ϵ為
ϵ
^
\hat{\epsilon}
ϵ^時其概率最大。
我們可以由圖看出當泛化錯誤率給定時,測試錯誤率與總樣本數的乘積即誤分類樣本數說一個二項分佈,我們對其進行假設檢驗,也稱為二項檢驗。書中給出原假設「 ϵ < = ϵ 0 \epsilon<=\epsilon_0 ϵ<=ϵ0」,那麼其備擇假設就是「 ϵ > ϵ 0 \epsilon>\epsilon_0 ϵ>ϵ0」,即原假設不成立時的對立結果,由此我們也可以得出這是一個右側單邊檢驗。書中直接給出了公式(最新的印刷有些不一樣) ϵ ˉ = m i n ϵ s . t . ∑ i = ϵ ∗ m + 1 m ( m i ) ∗ ϵ 0 i ∗ ( 1 − ϵ 0 ) m − i < α \bar{\epsilon}=min\ \epsilon\ \ s.t.\ \displaystyle\sum_{i=\epsilon*m+1}^{m} \begin{pmatrix} m \\ i \end{pmatrix}* \epsilon_0^{i}*(1-\epsilon_0)^{m-i}<\alpha ϵˉ=min ϵ s.t. i=ϵ∗m+1∑m(mi)∗ϵ0i∗(1−ϵ0)m−i<α
我們知道假設檢驗如果結果落入拒絕域範圍,那麼我們則可以拒絕原假設,所以對於上述公式也同樣的道理。用書上的圖來解釋
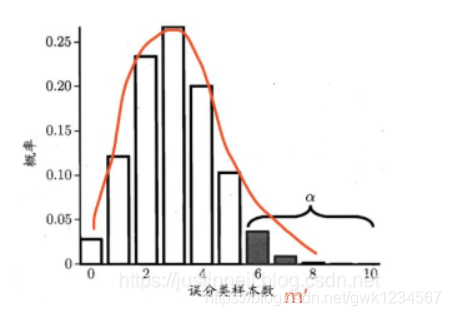
α \alpha α是顯著水平,1- α \alpha α是置信區間,我們可以將圖看作是普通的假設檢驗的單邊檢驗的函數影象,圖中的 α \alpha α區域看成拒絕域,其他部分看成是接受域,只要在 ϵ = ϵ 0 \epsilon=\epsilon_0 ϵ=ϵ0的情況下,該學習器的測試錯誤率 ϵ ^ \hat{\epsilon} ϵ^沒有落入拒絕域中,那麼我們就有1- α \alpha α的置信度認為學習器的泛化錯誤率 ϵ {\epsilon} ϵ小於 ϵ 0 {\epsilon_0} ϵ0,(因為 ϵ {\epsilon} ϵ是不知道的,我們只是假設),所以我們的關鍵就在於求出那個臨界值。
我們之前的概率值是在泛化錯誤率給定的情況下,學習器對
ϵ
^
\hat{\epsilon}
ϵ^的概率估計,我們要求假設接受的臨界值,相當於就是滿足概率相加的和小於
α
\alpha
α最小的那個測試錯誤率,書中給出的這個公式的作用也就是這個意思,我們可以看出圖中5就是那個臨界值,因為當誤分類樣本數為6,7,8,9,10的這些概率相加的和小於
α
\alpha
α,但若是加上5的這個概率值,那麼就會大於
α
\alpha
α,不滿足條件,所以5就是最小的臨界值。得到臨界值後,只要判斷其與測試錯誤率的大小即可。