一道題解釋樹形dp【此後無良辰】

題面描述

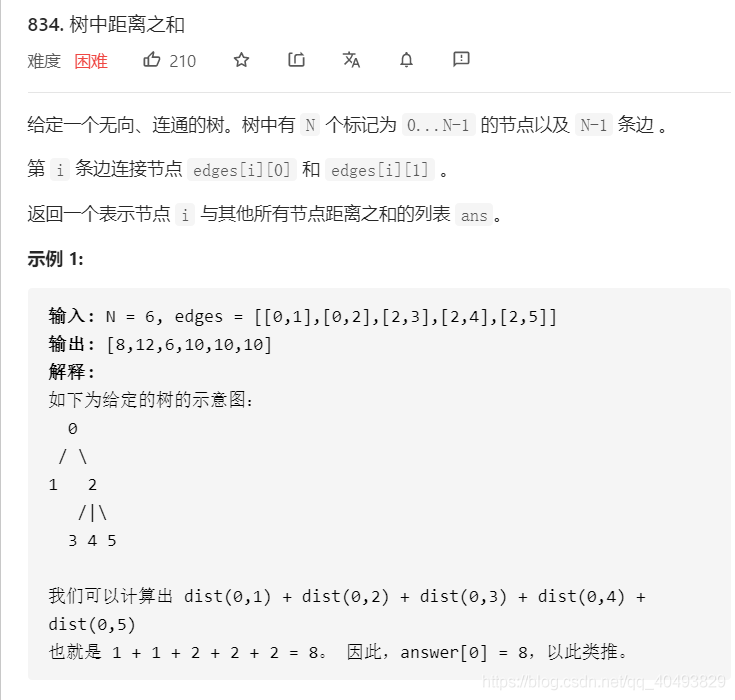
基本思路

首先一看題 死死的認為樹不就是圖嗎，最短路演演算法套上去不就得了嗎

然後寫了一個spfa和djstla

int spfa(int x,int N){//SPAF
    queue<int> q;
    for(int i=0;i<N;++i){
        dis[i]=inf;
        vis[i]=0;
    }
    
    q.push(x);
    vis[x]=1;dis[x]=0;
    while(!q.empty()){
        int u = q.front();q.pop();vis[u]=0;
        for(int i =e[u].first;i!=0;i=e[i].next){
            int v=e[i].v,w=e[i].w;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                if(!vis[v]){
                    q.push(v);
                    vis[v]=1;
                }
            }
        }
    }
    int tem_ans=0;
    for(int nums:dis){
        tem_ans+=nums;
    }
    return tem_ans;
}

///Djstla//
 template <class Compare>
    int Djstl(int x,int N, Compare comp)
    {
        priority_queue<int, vector<int>, Compare> q(comp);
        for(int i=0;i<N;++i){
            dis[i]=inf;
            vis[i]=0;
        }
        dis[x]=0;
        q.push(x);
        while(!q.empty())
        {
            int u=q.top();q.pop();
            if(!vis[u])
            {
                vis[u]=1;
                for(int i=e[u].first;i;i=e[i].next)
                {
                    int v=e[i].v,w=e[i].w;
                    dis[v]=min(dis[v],dis[u]+w);
                    q.push(v);
                }
            }
        }
        int tem_ans=0;
        for(int i=0;i<N;++i) tem_ans+=dis[i];
        return tem_ans;
    }

全部死在了第64個點…
題解來自於leetcode 題目

一看題解又是要命的dp，還是樹形dp，打比賽遇到我絕對甩給我隊友

dp為初始 通過dfs解決
換根優化時間複雜度

class Solution {
    int[] ans;
    int[] sz;
    int[] dp;
    List<List<Integer>> graph;

    public int[] sumOfDistancesInTree(int N, int[][] edges) {
        ans = new int[N];
        sz = new int[N];
        dp = new int[N];
        graph = new ArrayList<List<Integer>>();
        for (int i = 0; i < N; ++i) {
            graph.add(new ArrayList<Integer>());
        }
        for (int[] edge: edges) {
            int u = edge[0], v = edge[1];
            graph.get(u).add(v);
            graph.get(v).add(u);
        }
        dfs(0, -1);
        dfs2(0, -1);
        return ans;
    }

    //對根節點0 執行樹狀dp
    //u：當前節點，f：當前節點的「根」節點 
    public void dfs(int u, int f) {
        sz[u] = 1;
        dp[u] = 0;
        for (int v: graph.get(u)) {
            // 鄰接點不允許為u的根節點
            if (v == f) {
                continue;
            }
            dfs(v, u);
            dp[u] += dp[v] + sz[v];
            sz[u] += sz[v];
        }
    }

    //執行換根操作 
    public void dfs2(int u, int f) {
        // 記錄節點u的結果
        ans[u] = dp[u];
        // 對u的相鄰邊進行換根
        for (int v: graph.get(u)) {
            // 鄰接點不允許為u的根節點
            if (v == f) {
                continue;
            }
            // 暫時儲存 等待u換為v之後再還原
            // 因為u有很多v要換 這些值需要重複使用
            int pu = dp[u], pv = dp[v];
            int su = sz[u], sv = sz[v];

            //換根遞推式 
            dp[u] -= dp[v] + sz[v];
            sz[u] -= sz[v];
            dp[v] += dp[u] + sz[u];
            sz[v] += sz[u];

            // 記錄v的值 並且對v的鄰邊進行換根
            dfs2(v, u);

            // 還原
            dp[u] = pu;
            dp[v] = pv;
            sz[u] = su;
            sz[v] = sv;
        }
    }
}

提交oj