淺談共線性的產生以及解決方法(上篇——前世)

標題：淺談共線性的產生以及解決方法(上篇——前世)

1. 多元線性迴歸模型

線上性相關條件下，兩個或兩個以上解釋變數對一個被解釋變數的數量變化關係，稱之為多元線性迴歸分析，由多元線性迴歸分析得到的數學表示式稱為多元線性迴歸模型。
一般我們認為，多元線性迴歸問題中涉及的資料由被解釋變數Y和p個解釋變數$x_1$,$x_2$,$x_3$,…,$x_p$的n次觀測組成，如下表所示：
多元線性迴歸模型的一般形式為：y=${\beta }_0$+${\beta }_1$$x_1$+${\beta }_2$$x_2$+⋯+${\beta }_p$$x_p$+ε(其中ε為隨機誤差項，設定E(ε)=0，$Var(\epsilon )={\sigma }^2$。 ${\beta }_1$，${\beta }_2$，…，${\beta }_p$為迴歸係數，在迴歸係數估計時採用最小二乘估計方法，${\beta }_0$為常數)。
基本假定1 自變數$x_1$,$x_2$,$x_3$,…,$x_p$是確定性變數，不是隨機變數，又有設計矩陣是滿秩。
基本假定2 滿足高斯—馬爾科夫條件，即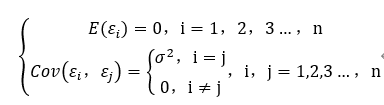
基本假定3 隨機誤差項服從正態分佈，即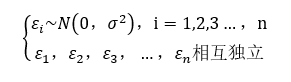

1.1 最小二乘估計

在多元線性迴歸模型中，我們通常使用最小二乘估計法來估計迴歸係數，得到迴歸係數的估計向量$\hat{\beta }=$(${\hat{\beta }}_0$，${\hat{\beta }}_1$，…，${\hat{\beta }}_p$)，${\hat{y}}_i$為迴歸值或者擬合值。
基本思想：要求實際觀測($x_i$,$y_i$)與直線上的點($x_i$,${\hat{y}}_i$)的偏離越小越好。

2. 多重共線性產生的原因及對模型的影響

解釋變數之間完全不相關的情況在科技、經濟、社會不斷髮展壯大的程序中是很難遇到的，因為涉及的自變數越多，我們很難判斷這些自變數之間相關與否，而且它們對研究物件有顯著影響。這樣的一組解釋變數有很大可能性是找不到的。客觀的說，當研究的問題涉及多個影響因素時，這多個因素之間或弱或強都有一定的相關性。當相關性較弱時，一般認為符合多元迴歸線性模型設計矩陣的基本假設；當有較強相關性時，就認為是一種違背多元線性迴歸模型基本假設的情形。
如果這種共線性問題得不到緩解，訓練模型得到的模型可能令人費解，引數估計的效應會由模型中的其他變數而導致其他自變數的引數改變，甚至符號改變。因此我們在做分析時，瞭解自變數間的關係非常重要。

2.1 什麼是共線性

假如存在不全為0的p+1個數$c_1$,$c_2$,$c_3$,…,$c_p$，使得

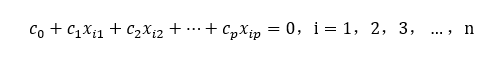
則自變數$x_1$,$x_2$,$x_3$,…,$x_p$之間存在著精確共線性。但在實際遇到的問題中，精確共線性是偶然事件。通常情況下，我們遇到的是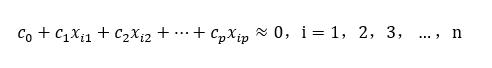當自變數$x_1$,$x_2$,$x_3$,…,$x_p$符合上述的數學關係時，我們稱自變數之間存在著多重共線性，存在一個常用但不完全合適的共線性程度度量指標，是樣本自變數之間的相關係數的平方，精確共線性對應的相關係數的平方等於1，非共線性對應的相關係數的平方等於0，近似共線性的相關係數平方介於0和1之間，值越大，表明兩個變數間近似共線性程度越大。
設因變數y的相關係數矩陣R=$X^{\prime }$X的特徵根為${\lambda }_1$≥${\lambda }_2$≥⋯≥${\lambda }_p$>0，又知 ${\sum }_{j=1}^p{\lambda }_j=p$
且${\lambda }_j$均非負，因此當某些${\lambda }_j$較大時，肯定會導致有一些${\lambda }_j$較小，但是其倒數必然很大。因此當$x_1$,$x_2$,$x_3$,…,$x_p$存在多重共線性時，${\lambda }_1$的值將變得較大，而${\lambda }_p$的值就會變得較小，雖然我們利用最小二乘估計方法得到的𝛽是β的無偏估計值，但是從均方誤差的意義上看，$\hat{\beta }$並不是β的最優估計。
利用最小二乘法估計值$\hat{\beta }$的均方誤差為:

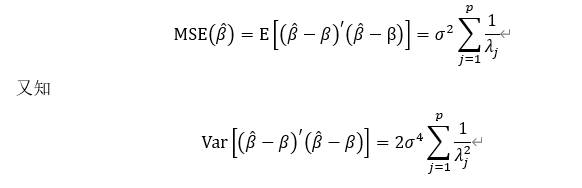
若記$\Vert \hat{\beta }-\beta \Vert =\sqrt{{(\hat{\beta }-\beta )}^{\prime }(\hat{\beta }-\beta )}$為向量$\hat{\beta }-\beta$的長度，從向量$\hat{\beta }-\beta$長度平方的期望值和方差上可以看出它們都依賴特徵根，所以當$x_1$,$x_2$,$x_3$,…,$x_p$存在多重共線性時，雖然用普通最小二乘估計能夠得到迴歸引數的無偏估計值，但向量$\hat{\beta }-\beta$的長度的均值將變得很大，其波動程度也會變大，這樣會導致迴歸係數的置信區間變寬，從而使得估計值不準確，模型的準確度也會嚴重下降，進而致使在迴歸方程整體高度顯著時，一些迴歸係數通不過顯著性檢驗，迴歸係數的正負號也有可能出現倒置，使得不能正確解釋自變數對因變數的影響程度，甚至導致估計量的實際意義無法解釋。
因此如自變數之間的共線性診斷和削弱是做模型訓練中不可或缺的一個過程。