動態規劃：將一個問題拆成幾個子問題，分別求解這些子問題，即可推斷出大問題的解。

判斷一個問題能否使用DP解決：能將大問題拆成幾個小問題，且滿足無後效性、最優子結構性質

DP的核心思想：儘量縮小可能解空間。

暴力做法是列舉所有的可能解，這是最大的可能解空間。
DP是列舉有希望成為答案的解。這個空間比暴力的小得多。

參考阮行止的回答

例1、青蛙跳臺階問題

題目連結

思想

對該問題進行抽象，n個階梯，每個階梯都代表一個位置，然後將這個n個位置相連（只能用長度為1和2的線）

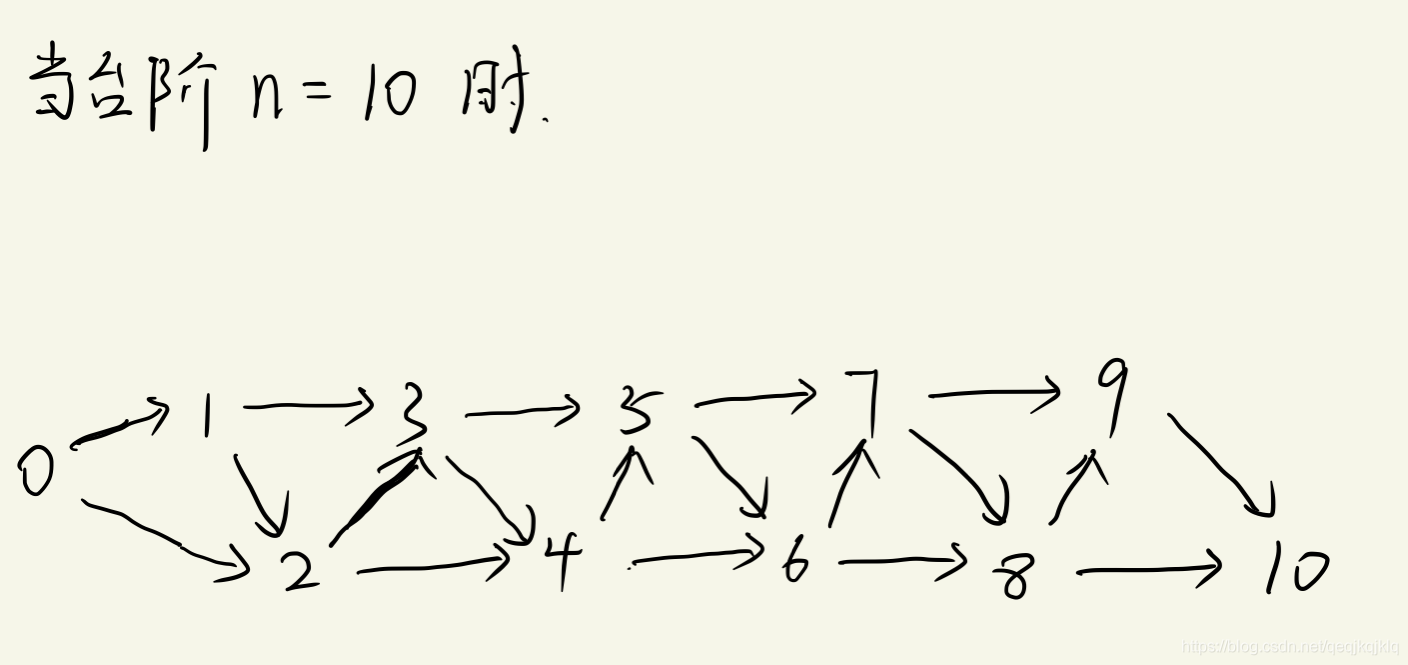
這個問題就轉化成了從 位置0 到 位置10 有幾種不同的路可以走？

遞推關係：dp[n] = dp[n-1] + dp[n-2];

比如7到10有幾種走法=8到10的走法+9到10的走法

遞推結果可以由下面這個陣列說明

參考牛岱的回答

程式碼

class Solution {
public:
    int numWays(int n) {
        vector<int> dp(n+1,1);
        for(int i=2;i<=n;i++){
            dp[i]=(dp[i-1]+dp[i-2])%1000000007;
        }
        return dp[n];
    }
};

例2、最長上升子序列

題目連結

思想

方法1，	O(n2)做法

參考

程式碼

對應方法1

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> dp(nums.size());
        for(int i=0;i<nums.size();i++){
            dp[i]=1;
            for(int j=0;j<i;j++){
                if(nums[j]<nums[i]&&dp[j]+1>dp[i])
                    dp[i]=dp[j]+1;
            }
        }
        //這裡我呼叫逆序函數，返回首部不曉得為啥不行
        // sort(dp.rbegin(),dp.rend());
        // return dp[0];
        int res=0;
        for(int i=0;i<dp.size();i++){
            if(res<dp[i])
                res=dp[i];
        }
        return res;
    }
};

二分查詢解法

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        //二分查詢解法
        vector<int> top=nums;
        // 牌堆數初始化為 0
        int piles = 0;
        for (int i = 0; i < nums.size(); i++) {
            // 要處理的撲克牌
            int poker = nums[i];
            /***** 搜尋左側邊界的⼆分查詢 *****/
            int left = 0, right = piles;
            while (left < right) {
                int mid = (left + right) / 2;
                if (top[mid] > poker) {
                    right = mid;
                } 
                else if (top[mid] < poker) {
                    left = mid + 1;
                } 
                else {
                    right = mid;
                }
            }  
            // 沒找到合適的牌堆， 新建⼀堆
            if (left == piles) piles++;
            // 把這張牌放到牌堆頂
            top[left] = poker;
        }
        // 牌堆數就是 LIS ⻓度
        return piles;
    }
};

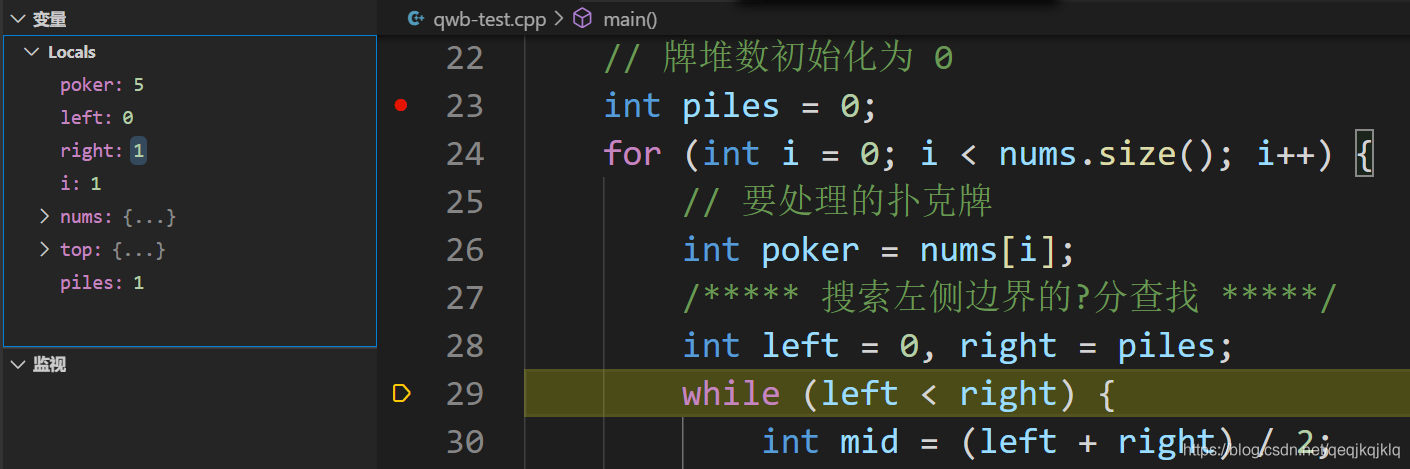
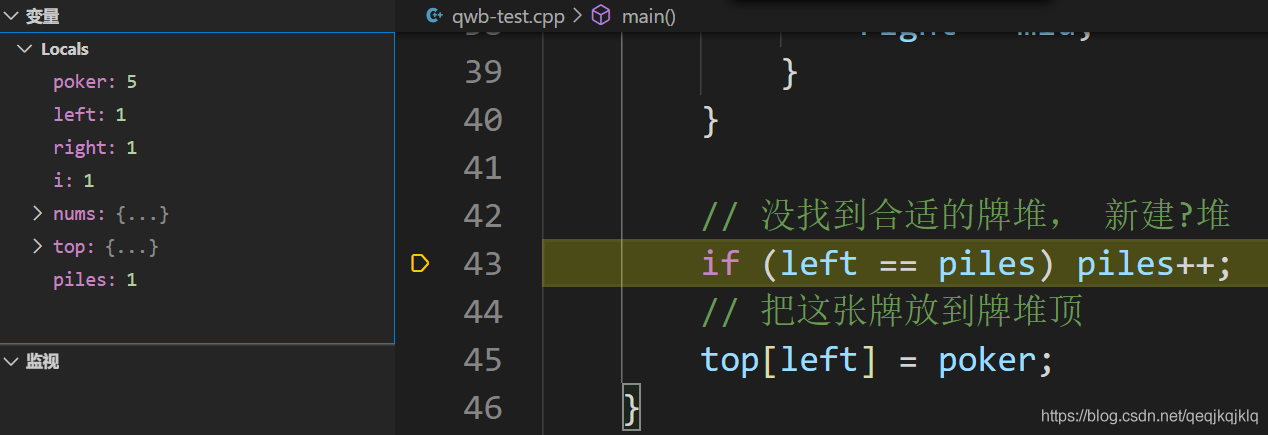
對上訴二分查詢程式碼進行分析
序列為2 5 3 4 1 7 6

下圖為i=0時剛進入迴圈

進while迴圈前

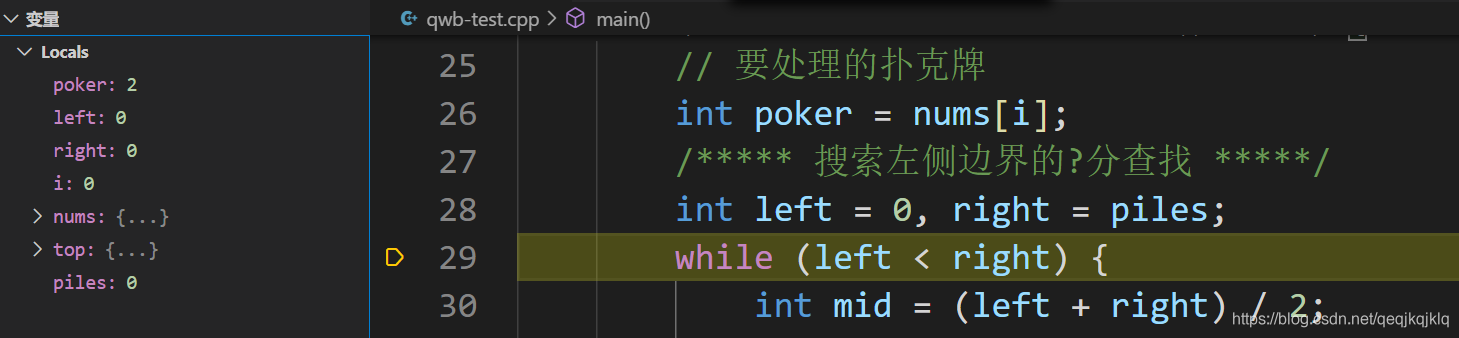
i=1

例3、剪繩子

題目連結

思想

參考出處

動態規劃5步走

1. 判題題意是否為找出一個問題的最優解
2. 從上往下分析問題，大問題可以分解為子問題，子問題中還有更小的子問題
3. 從下往上分析問題 ，找出這些問題之間的關聯（狀態轉移方程）
4. 討論底層的邊界問題
5. 解決問題（通常使用陣列進行迭代求出最優解）

由5步走可知

1. 判題題意是否為找出一個問題的最優解 看到字眼是「可能的最大乘積是多少」，由此判斷是求最優解問題，可以用動態規劃解決；

2. 從上往下分析問題，大問題可以分解為子問題，子問題中還有更小的子問題。 題目中舉了個例子：當繩子的長度為8時，我們把它剪成長度分別為2,3,3的三段，此時得到的最大乘積是18；我們可以從這裡開始突破，把長度為8繩子的最大乘積分解為數個子問題，長度為8我們可以把它看成長度為1和7的繩子的和，或者長度為2和6的繩子的和，或者長度為3和5的繩子的和and so on! 到這裡，相信大家已經看到一絲真理了吧？

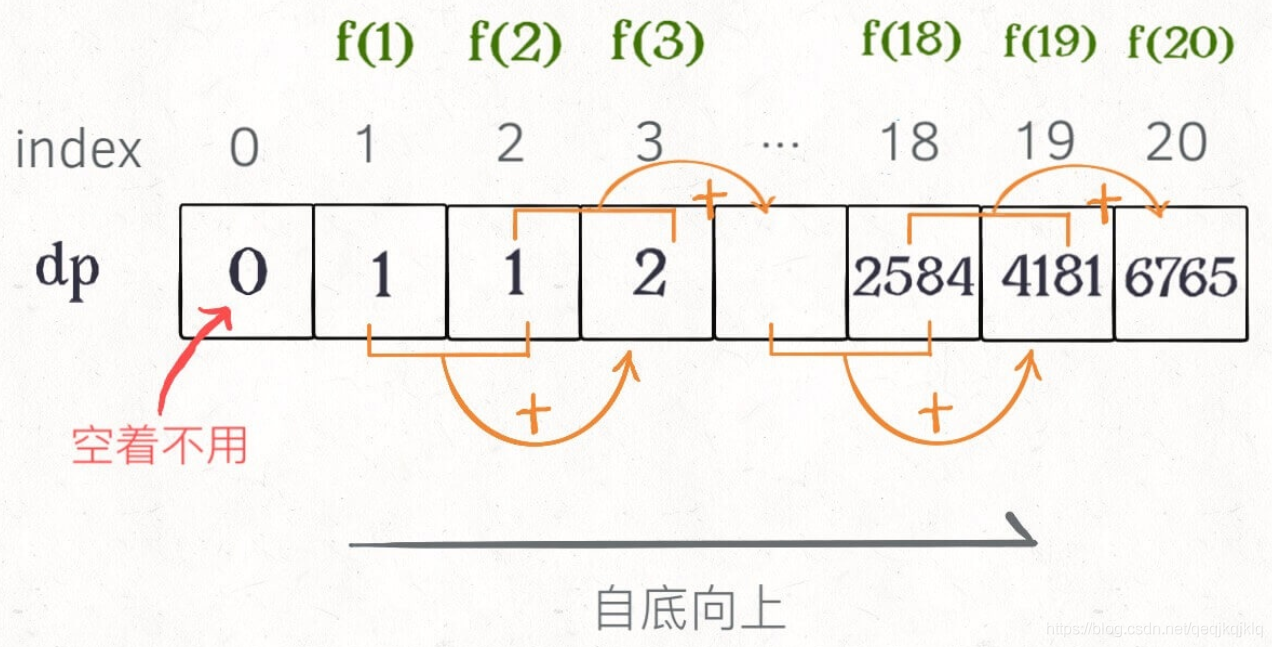
3. 從下往上分析問題 ，找出這些問題之間的關聯（狀態轉移方程） 在第二點時，我們已經從上到下分析問題了，現在我們要從下往上分析問題了。分析可知， f(8)的值就是f(1)*f(7),f(2)*f(6),f(3)*f(5),f(4)*f(4)它們之中的最大值，即f(8) =
   Max{f(1)*f(7),f(2)*f(6),f(3)*f(5),f(4)*f(4)}
   只要知道f(1)到f(7)的值就能求出f(8)；對於f(7)，只要知道f(1)到f(6)的值就能求出f(7)；對於f(6)，只要知道f(1)到f(5)的值就能求出f(6)；以些類推，我們只要知道前幾個邊界的值，就能一步步迭代出後續的結果!
   狀態轉移方程： f(n)=Max{f(n-i)*f(i)} i={1,2,3,…,n/2}

4. 討論底層的邊界問題 底層的邊界問題說的就是最小的前幾個數值的f(n)的值，本題中就是f(0)、f(1)、f(2)、f(3)的值 。
   對於f(0)，長度為0的繩子，沒辦法剪，沒有意義
   對於f(1)，長度為1的繩子，沒辦法剪，設為1
   對於f(2)，長度為2的繩子，只有一種剪法，剪成兩段長度為1的繩子，但剪後的乘積為1，比自身更小；如果不是求自身的值，要求乘積最大值的話就沒必要剪。
   對於f(3)，長度為3的繩子，只有一種剪法，剪成兩段長度為1和2的繩子，但剪後的乘積為2，比自身更小；如果不是求自身的值，要求乘積最大值的話也沒必要剪。

程式碼

Java版本

public static int cutting(int n) {
        //長度小於等等於1沒辦法剪
        if(n <= 1)
            return 0;
        //對於f(2)，長度為2的繩子，只有一種剪法，剪成兩段長度為1的繩子，剪後的乘積為1
        if(n == 2)
            return 1;
        //對於f(3)，長度為3的繩子，只有一種剪法，剪成兩段長度為1和2的繩子，但剪後的乘積為2
        if(n == 3)
            return 2;
        int max = 0;
        //陣列用於儲存繩子乘積最大值
        int value[] = new int[n + 1];
        value[0] = 0;
        value[1] = 1;
        //剪後的乘積為1，比自身更小；如果不是求自身的值，要求乘積最大值的話就沒必要剪
        value[2] = 2;
        //剪後的乘積為2，比自身更小；如果不是求自身的值，要求乘積最大值的話也沒必要剪
        value[3] = 3;
        //從f(4)開始迭代
        for(int i = 4;i <= n; i++) {
            max = 0;
            for(int j = 1;j <= i/2; j++) {
                int val = value[j] * value[i - j];
                max = val > max ? val : max;
            }
            value[i] = max;
        }
        max = value[n];
        return max;
}

C++版本

class Solution {
public:
    int cuttingRope(int n) {
        vector<int> dp(n+1,0);
        dp[0]=1;
        for(int i=1;i<=(n+1)/2;i++){
            for(int j=i;j<=n;j++){
                dp[j]=max(dp[j],dp[j-i]*i);
            }
        }
        return dp[n];
    }
};

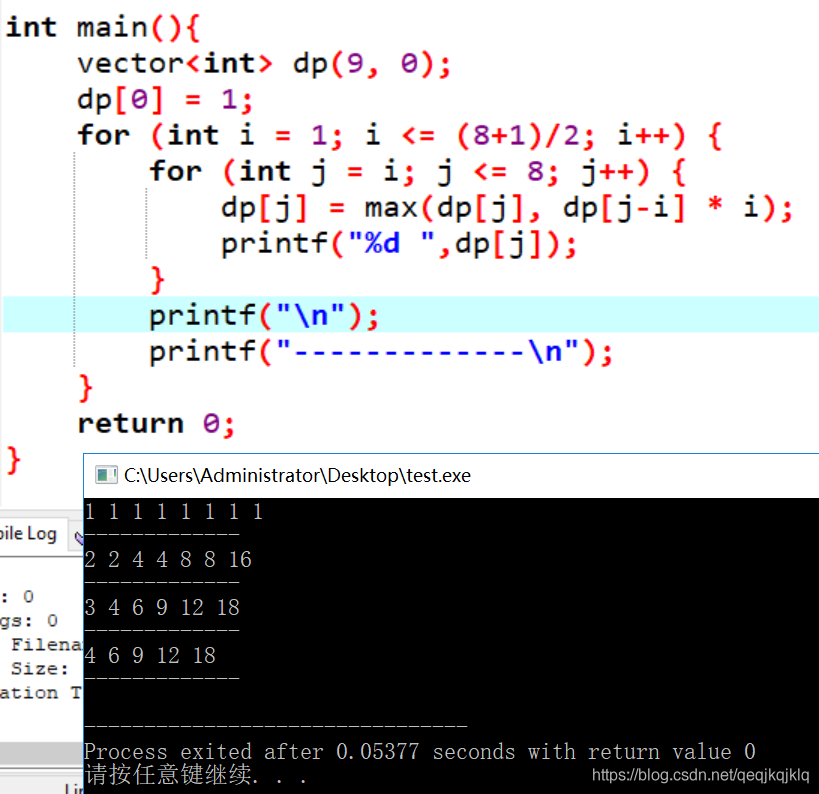
下面是上訴的c++程式碼的執行過程

北大OJ
PAT
codeup
C++的常用函數