機器學習之梯度下降演演算法(python實現)

一點關於學習梯度下降演演算法的感受

首先就個人體驗來看，在本科期間在學習運籌與優化這門課程就接觸過梯度下降演演算法，那個時候就是單一的求一個具體多變數函數的最小值問題。現在在機器學習裡面的梯度下降演演算法更多的是根據訓練資料集去找到一個合適的擬合函數，那麼怎麼樣才能找到一個擬合度高的函數使之在測試集上有較好的泛化能力，此時就需要定義一個擬合函數模型和一個損失函數，當損失函數的取值最小時就可以得到這個在訓練集擬合度好的函數了。得到這個函數模型之後就可以去做相關測試資料的預測了。其中求損失函數的最小值過程就是我們現在所講的梯度下降演演算法迭代過程了。

一、梯度下降的相關概念

在詳細瞭解梯度下降的演演算法之前，我們先看看相關的一些概念。

1. 步長（Learning rate）：步長決定了在梯度下降迭代的過程中，每一步沿梯度負方向前進的長度。用上面下山的例子，步長就是在當前這一步所在位置沿著最陡峭最易下山的位置走的那一步的長度。

2.特徵（feature）：指的是樣本中輸入部分，比如2個單特徵的樣本$（x^{(0)},y^{(0)}）,（x^{(1)},y^{(1)}）$,則第一個樣本特徵為$x^{(0)}$，第一個樣本輸出為$y^{(0)}$。

3. 假設函數（hypothesis function）即擬合函數：在監督學習中，為了擬合輸入樣本，而使用的假設函數，記為$h_{\theta }(x)$。比如對於單個特徵的m個樣本$（x^{(i)},y^{(i)}）(i=1,2,...m)$,可以採用擬合函數如下： $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$。

4. 損失函數（loss function）：為了評估模型擬合的好壞，通常用損失函數來度量擬合的程度。損失函數極小化，意味著擬合程度最好，對應的模型引數即為最優引數。線上性迴歸中，損失函數通常為樣本輸出和假設函數的差取平方。比如對於m個樣本$（x_i,y_i）(i=1,2,...m)$,採用線性迴歸，損失函數為：$$J({\theta }_0,{\theta }_1)=\sum _{i=1}^m(h_{\theta }(x_i)-y_i{)}^2$$
　　　　其中$x_i$表示第i個樣本特徵，$y_i$表示第i個樣本對應的輸出，$h_{\theta }(x_i)$為假設函數。

二、梯度下降的詳細演演算法(代數方式描述)

1. 先決條件： 確認優化模型的假設函數和損失函數。

比如對於線性迴歸，假設函數表示為 $$h_{\theta }(x_1,x_2,...x_n)={\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$$, 其中${\theta }_i$(i = 0,1,2… n)為模型引數，$x_i$ (i = 0,1,2… n)為每個樣本的n個特徵值。這個表示可以簡化，我們增加一個特徵$x_0$=1 ，這樣$h_{\theta }(x_0,x_1,...x_n)=\sum _{i=0}^n{\theta }_i{x}_i$。

同樣是線性迴歸，對應於上面的假設函數，損失函數為：$$J({\theta }_0,{\theta }_1...,{\theta }_n)=\frac{1}{2m}\sum _{j=1}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j{)}^2$$

2. 演演算法相關引數初始化：主要是初始化${\theta }_0,{\theta }_1...,{\theta }_n$,演演算法終止距離ε以及步長α。在沒有任何先驗知識的時候，我喜歡將所有的θ初始化為0， 將步長初始化為0.001。在調優的時候再 優化。

3. 演演算法過程：

1）確定當前位置的損失函數的梯度，對於${\theta }_i$,其梯度表示式如下：$$\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1...,{\theta }_n)$$
2）用步長乘以損失函數的梯度，得到當前位置下降的距離，即$\alpha \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1...,{\theta }_n)$對應於前面登山例子中的某一步。

3）確定是否所有的${\theta }_i$,梯度下降的距離都小於ε，如果小於ε則演演算法終止，當前所有的θi(i=0,1,…n)即為最終結果。否則進入步驟4.

4）更新所有的$\theta$，對於${\theta }_i$，其更新表示式如下。更新完畢後繼續轉入步驟1.$${\theta }_i={\theta }_i-\alpha \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1...,{\theta }_n)$$
下面用線性迴歸的例子來具體描述梯度下降。假設我們的樣本是$(x_1^{(0)},x_2^{(0)},...x_n^{(0)},y_0),(x_1^{(1)},x_2^{(1)},...x_n^{(1)},y_1),...(x_1^{(m)},x_2^{(m)},...x_n^{(m)},y_m)$,損失函數如前面先決條件所述：$$J({\theta }_0,{\theta }_1...,{\theta }_n)=\frac{1}{2m}\sum _{j=0}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j{)}^2$$

則在演演算法過程步驟1中對於θi 的偏導數計算如下：

$$\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1...,{\theta }_n)=\frac{1}{m}\sum _{j=0}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j)x_i^{(j)}$$
　　　　由於樣本中沒有$x_0$上式中令所有的$x_0^j$為1.

步驟4中θi的更新表示式如下：
$${\theta }_i={\theta }_i-\alpha \frac{1}{m}\sum _{j=0}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},...x_n^j)-y_j)x_i^{(j)}$$
　　　　從這個例子可以看出當前點的梯度方向是由所有的樣本決定的，加$\frac{1}{m}$是為了好理解。由於步長也為常數，他們的乘機也為常數，所以這裡$\alpha \frac{1}{m}$可以用一個常數表示。

三、程式碼實現(python)和相關效果圖

說不多說，到了大家最關心的程式碼實現的部分了，其實上面所說的演演算法過程既是批次梯度下降演演算法的過程。還有就是說實話這是我認真寫過的有詳細註釋的程式碼了，歐克，肝就完了！
下面展示全部程式碼 。

import numpy as np
import matplotlib.pyplot as plt

# 定義資料集的大小為30
m = 30
# x0為1
x = np.ones((m, 1))
# 設定三個特徵向量取值陣列的拼接
x = np.concatenate((x, np.arange(1, m + 1).reshape(m, 1), np.arange(2, 2 * m + 1, 2).reshape(m, 1)), axis=1)
y_data = np.loadtxt('data.txt', delimiter=',')
# 從陣列提取y的取值
y = np.array(y_data[:, 1][0:30]).reshape(m, 1)
# 設定學習效率
alpha = 0.001
# 設定模型引數theta的初始迭代點(一般都是從0開始)
theta = np.zeros((3, 1))
# 分別定義一個儲存損失函數值和迭代次數的列表
costlist, num = [], []


# 定義一個代價函數
def costfunction(theta, x, y):
    error = np.dot(x, theta) - y
    return (1 / 2 * m) * (np.dot(error.T, error))


# 定義一個梯度迭代的函數，即偏導數部分
def gradientdescent(theta, x, y):
    error = np.dot(x, theta) - y
    return (1 / m) * (np.dot(x.T, error))


# 下降迭代過程函數
def GDworkfunction(theta, alpha, x, y):
    gd = gradientdescent(theta, x, y)
    # 迭代10萬次終止
    for i in range(100000):
        theta = theta - alpha * gd
        cost1 = costfunction(theta, x, y)
        costlist.append(cost1)
        num.append(i)
        gd = gradientdescent(theta, x, y)
    return theta


consulttheta = GDworkfunction(theta, alpha, x, y)
print('cost值取得最小時的函數為：y={}+{}*x1+{}*x2'.format(consulttheta[0], consulttheta[1], consulttheta[2]))
cost = costfunction(consulttheta, x, y)[0][0]
print('此時的最小損失值為{}'.format(cost))
costlist1 = []
# 對cost值進行特徵縮小，縮小的範圍自己主觀決定，怎麼方便怎麼來！
for j in costlist:
    costlist1.append(j / 4500)

plt.figure(num=3, figsize=(8, 5))
# 在繪圖時，需要對cost值進行降維成一維，因為儲存的是二維的陣列
plt.plot(num, np.squeeze(np.array(costlist1)))
plt.xlim((1, 80000))
plt.ylim(1, 10)
plt.xlabel('iterate_nums')
plt.ylabel('costvalue')
# 設定x軸刻度表示範圍
my_x_ticks = np.arange(1, 80000, 6000)
plt.xticks(my_x_ticks)
plt.savefig('F:\\DataBuilding\\BGD\\BGD.png')  # 儲存圖片
plt.show()

import sys; print('Python %s on %s' % (sys.version, sys.platform))
sys.path.extend(['F:\\pycharmspace\\pycharm-project\\日常dome', 'F:/pycharmspace/pycharm-project/日常dome'])
PyDev console: starting.
Python 3.8.3 (tags/v3.8.3:6f8c832, May 13 2020, 22:37:02) [MSC v.1924 64 bit (AMD64)] on win32
runfile('F:/pycharmspace/pycharm-project/日常dome/Algorithm/MygradientDecentdome.py', wdir='F:/pycharmspace/pycharm-project/日常dome/Algorithm')
cost值取得最小時的函數為：y=[7.51769165]+[0.01716882]*x1+[0.03433763]*x2
此時的最小損失值為18629.353835283197

emmm，做完之後就覺得這個損失值的最小值大的驚人，可能是資料選取的資料跨度大，不過不影響實際演演算法目的。接下來上迭代次數和損失函數的效果圖：

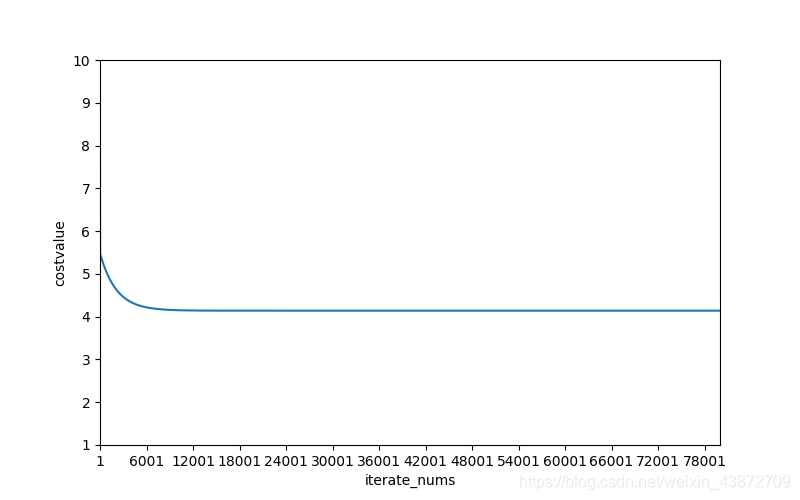
就這張圖來說，當下降迭代次數到達6000次的時候就開始逐漸趨向最小損失值了。下面附上$y_i$的資料集

17.592,9.1302,11.854,6.8233,11.886,4.3483,12,6.5987,3.8166,3.2522,15.505,3.1551,7.2258,0.71618,3.51295.3048,0.56077,3.6518,5.3893,3.1386,21.767,4.263,5.1875,3.0825,22.638,13.501,7.0467,14.692,24.147

四、總結

梯度下降演演算法機器學習的求最優值這方面無論怎麼改動都有不可代替的優勢，因為其穩定，效率較高，且結果一定會得出來且基本都接近或者就是最優解，當然我們也可以用資料分析神器SPSS來做一個的分析結果來驗證程式碼跑出來的結果是否一致。這個大家可以做做看，感興趣的可以把我這個程式碼跑跑看。
這是我第一次自寫的部落格，寫的比較不怎麼成熟，以後我會繼續更新一些有關機器學習的演演算法，比如說求全域性最優值的隨機遊走演演算法，和遺傳演演算法等…