Pytorch黑盒攻擊音訊分類網路
2020-10-07 13:00:28
基於Pytorch的黑盒攻擊
攻擊的模型
- 攻擊的型別是無目標攻擊,改天再嘗試下目標攻擊
- 攻擊的模型是我之前訓練好的一個分類網路參考下面這篇部落格
-
https://blog.csdn.net/qq_37633207/article/details/108926652
攻擊的效果
- 攻擊效果還不錯,基本上幾次迭代就攻擊好了,可能是自己訓練的網路比較垃圾,自己訓練的分類網路精度為93.499%,我太難了
- 先來兩張攻擊的效果圖
- 首先是原來的音訊,我這裡是隨機選取一個音訊
波形圖對比
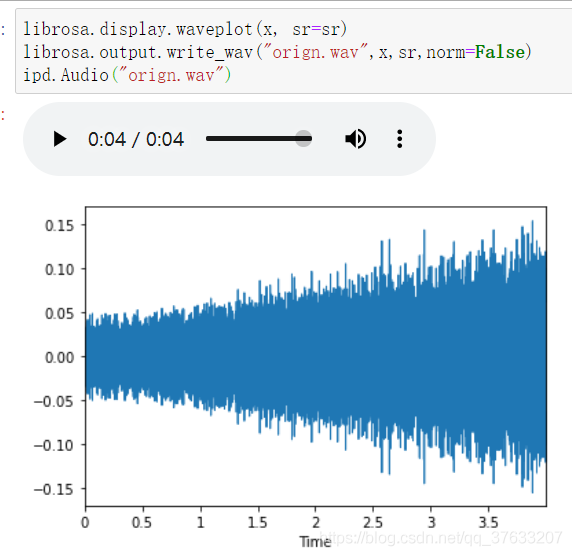
- 再來一張圖片,由於差距極小,所以我特意把攻擊成果的音訊直接畫在源音訊上,仔細就能看見他們之間的差距
- 那些黃色末端的藍色就是他們攻擊攻擊音訊與原有音訊的差距,這種差距對於人耳來說是不可聞的
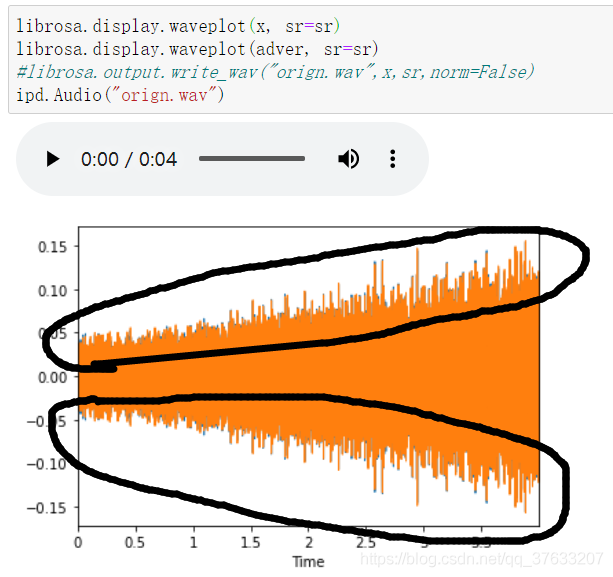
頻譜圖對比
- 上面一張為原音訊,下面一張為增加擾動後的音訊,也就高分貝有略微區別
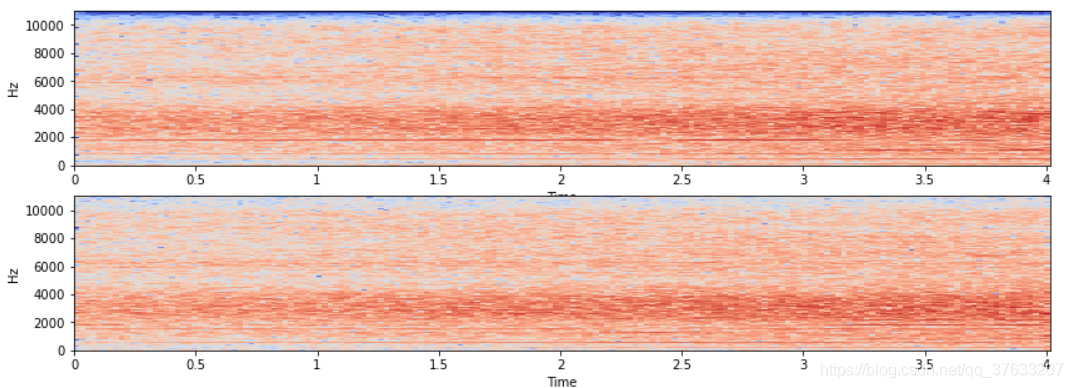
攻擊迭代過程
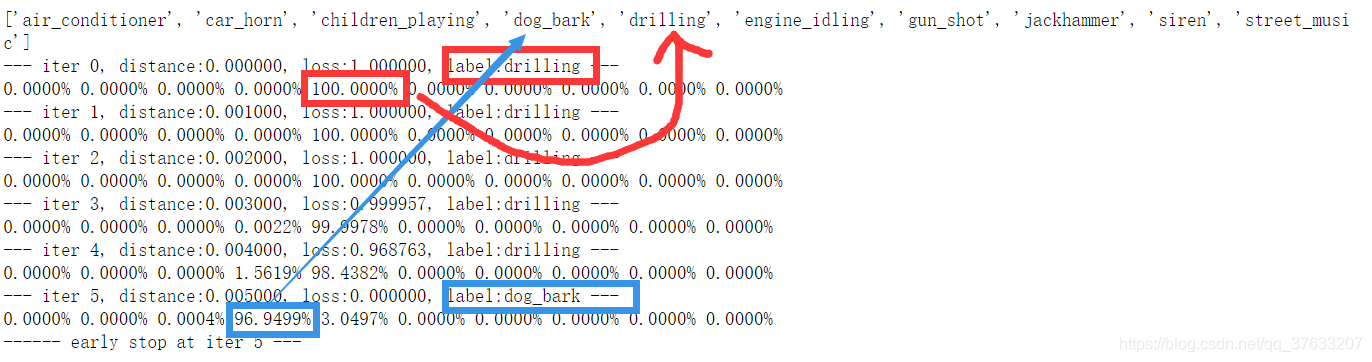
- 這是我輸出的迭代過程,最上面一排是對應score的標籤,兩個紅色的框代表了初始的label以及初始時候的最佳得分,可以看見這個音訊被100%的分類為了drilling(電鋸聲音),經過5次迭代以後的藍色框,分別代表攻擊成功後的label 以及最佳得分,可以看見這段音訊被分類為狗叫的概率為96.9499%,而且僅僅迭代了5次,神經網路是多麼的脆弱(或者說我寫的分類網路是多麼的垃圾\手動狗頭)
- 神經網路的魯棒性和決策邊界的問題現在也沒人能說明白問題,越魯棒必然可以接受越多量的輸入擾動,資料集不可能面面俱到,訓練的決策邊界也一定不是真正的決策邊界,越多量的輸入擾動又能必然帶來越多的影響,這樣魯棒性反而成為攻擊的弱點,魯棒性真的魯棒嘛?
增加的擾動
- 由於資料的太過密集,所以列印出來的擾動是下面這個樣子的,看起來好像都是一樣
- 實際上這些資料還是不一樣的,只是這邊有將近9w個取樣點所以畫出來看起來就像是沒有變化的,我們下面列印出來看看這些資料,資料太多就只列印了頭和尾。

攻擊的思路以及程式碼
完整程式碼如下
- 其實更推薦jupyter 因為IPython.display很好用
- 這邊我程式碼完全從我的jupyter拷貝過來,可能IPython模組會不能用?
- 本來想寫個流程圖的,實在太麻煩了,什麼流程圖都沒有程式碼本身細節。
- 如果一些路徑或者檔案獲取看不懂,可以參考我的另一篇部落格,因為這兩篇部落格是無縫銜接的
-
https://blog.csdn.net/qq_37633207/article/details/108926652
- 我的程式碼中有大量的註釋,特別注意下最後我在呼叫attack時候集中描述了下attack的引數的含義,這些引數對於理解我程式碼的含義的過程很重要
import torch
import torch.nn as nn
import torch.nn.functional as F
import random
import librosa
import librosa.display
import IPython.display as ipd
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import os
import copy
import pickle
"""
定義分類網路用於恢復
"""
class Classify(nn.Module):
def __init__(self):
super(Classify,self).__init__()
self.fc1=nn.Linear(40,64)
self.dp=nn.Dropout(0.03)
self.fc2=nn.Linear(64,20)
self.fc3=nn.Linear(20,10)
def forward(self,x):
x=F.relu(self.fc1(x))
x=self.dp(x)
x=F.relu(self.fc2(x))
x=F.relu(self.fc3(x))
x=F.softmax(x,dim=1)
return x
"""
此函數用於隨機獲取一條音訊的各種資訊
"""
def get_x_sr_label_random():
train=pd.read_csv("train/train.csv",sep=',')
i=random.choice(train.index)
audio_name=train.ID[i]
path = os.path.join("train", 'Train', str(audio_name) + '.wav')
print('Class: ', train.Class[i])
label_name=train.Class[i]
label_class=sorted(train.Class.value_counts().index.tolist())
label_index=label_class.index(label_name)
x, sr = librosa.load('train/Train/' + str(train.ID[i]) + '.wav')
return x,sr,label_name,label_index,label_class
"""
此函數用於獲得一批加噪後的音訊,將來會用於計算平均梯度
"""
def get_noise_audio(audio,adv_sample_nums=10,sigma=0.02):#這裡的audio是個numpy.array([[xx,xx,xx....]])型別的資料
N=audio.size#獲取元素個數
noise_pos=np.random.normal(size=(adv_sample_nums//2,N))
noise=np.concatenate((noise_pos,-1*noise_pos),axis=0)
noise = np.concatenate((np.zeros((1, N)), noise), axis=0)
noise_audios = sigma * noise + audio
return noise_audios,noise#這個你懂的[[][][]]
"""
此函數用於把輸入資料計算mfcc特徵後,輸入網路計算得分
"""
def get_score(model,x,sr):#x是個二維的np[[],[],[],[]]
input_datas=np.mean(librosa.feature.mfcc(y=x[0], sr=sr, n_mfcc=40).T,axis=0)
input_datas=input_datas[np.newaxis,:]
#print(input_datas.shape)
for item in x[1:]:
temp_data=np.mean(librosa.feature.mfcc(y=item, sr=sr, n_mfcc=40).T,axis=0)
temp_data=temp_data[np.newaxis,:]
input_datas = np.concatenate((input_datas,temp_data),axis=0)
model.eval()
model.to('cpu')
#print(input_datas.shape)
"""
注意輸入網路需要torch。Tensor型別資料,返回的也是tensor 所以都要型別轉換
"""
with torch.no_grad():
scores=model(torch.from_numpy(input_datas))
return scores.numpy()
"""
這個函數返回四個值
final_loss是除了當前的audio以外加擾動後的noise_aduios的平均損失 是一個具體的數值
estimate_grad的計算公式如下np.mean(loss * noise, axis=0, keepdims=True) / sigma 是一個(1,N)的向量
adver_loss是當前的audio的損失 是一個(1,1)向量
score則是當前迭代的audio的分數 是一個(1,10)的向量
"""
def get_grad(noise_audios,noise,scores,loss,sigma):
adver_loss = loss[0]#這是原來當前音訊的loss 是個(1,)的shape
score = scores[0]#原來的socre
loss=loss[1:,:]
noise = noise[1:,:]#去除原來樣本的noise
final_loss=np.mean(loss)
estimate_grad = np.mean(loss * noise, axis=0, keepdims=True) / sigma # grad的格式是1*N [xx,xx,x,x...]
return final_loss,estimate_grad,adver_loss,score
"""
整合函數attack
這個函數輸入的audio是個np.array([xx,xx,......])型別
"""
#傳入的audio是個[xx,xx,xx,xx]
def attack(model,label_class,audio,sr,true_index,sigma=0.001,max_iter=1000,epsilon=0.002,
max_lr=0.001,min_lr=1e-6,adv_sample_nums=10,
adver_thresh=0,momentum=0.9,plateau_length=5,plateau_drop=2.):
#為audio增加一個batch__size維度
audio=audio[np.newaxis,:]#[[]]
adver=copy.deepcopy(audio)
lower=np.clip(audio-epsilon,-1.,1.)
upper=np.clip(audio+epsilon,-1.,1.)
lr=max_lr
estimate_grad=0
cp_global=[]#存放結果
last_ls=[]#存放近幾次的損失 存放個數與plateau_length有關
for iter in range(max_iter):
cp_local=[]
#上一次的估計梯度
pre_grad = copy.deepcopy(estimate_grad)
#獲得加噪後的audios 以及未乘上sigma的noise
noise_audios,noise=get_noise_audio(adver,adv_sample_nums,sigma)# shape (adv_smaple_nums+1,N)、(adv_smaple_nums,N)
#計算noise_audios 輸入的分數
scores=get_score(model,noise_audios,sr)#scores (adv_sample_nums+1,10)
#根據noise_audios的得分計算出每個noise_audio的loss
loss=loss_fn(scores,true_index,adver_thresh=adver_thresh) #loss (adv_sample_nums+1,1)
#final_loss是除了當前的audio以外加擾動後的noise_aduios的平均損失 是一個具體的數值
#estimate_grad的計算公式如下np.mean(loss * noise, axis=0, keepdims=True) / sigma 是一個(1,N)的向量
#adver_loss是當前的audio的損失 是一個(1,)的numpy.array()物件
#score則是當前迭代的audio的分數 是一個(1,10)的向量
final_loss,estimate_grad,adver_loss,score = get_grad(noise_audios,noise,scores,loss,sigma)
#計算l無窮範數的距離
distance=np.max(np.abs(audio-adver))
#計算當前的label
now_label=label_class[np.argmax(score)]
print("--- iter %d, distance:%f, loss:%f, label:%s ---" % (iter, distance, adver_loss,now_label))
for s in score:
print("{:.4%}".format(s),end=' ')
print('')
if adver_loss == -1 * adver_thresh:
print("------ early stop at iter %d ---" % iter)
cp_local.append(distance)
cp_local.append(adver_loss)
cp_local.append(score)
cp_local.append(0.)
cp_global.append(cp_local)
break
#根據動量以及估計梯度調整梯度
#print(estimate_grad)
estimate_grad = momentum * pre_grad + (1.0 - momentum) * estimate_grad
#下面是根據損失調整學習率
last_ls.append(final_loss)
last_ls = last_ls[-plateau_length:]#僅僅記錄最後的5個final_loss
if last_ls[-1] > last_ls[0] and len(last_ls) == plateau_length:#如果損失反而上升了 有可能學習率過大
if lr > min_lr:#如果學習率還可以下降
lr = max(lr / plateau_drop, min_lr)
last_ls = []#重新開始記錄final_loss
#更新adver
#print(estimate_grad)
adver-=lr*np.sign(estimate_grad)
#print(abs(audio-adver))
adver=np.clip(adver,lower,upper)
cp_local.append(distance)
cp_local.append(adver_loss)
cp_local.append(score)
cp_global.append(cp_local)
with open("cp_global.plk", "wb") as f:
pickle.dump(cp_global, f)
return adver
"""
接下來就是初始化一些基本的引數了
"""
pretrained_model="torchmodel.pth"
model=torch.load(pretrained_model)#初始化模型
x,sr,label_name,label_index,label_class=get_x_sr_label_random()#獲得音訊的基本資訊
"""
集中解釋下這些引數
sigma是擾動的係數,不管是librosa讀取的資料或者說是我們產生的擾動都必須限制在[-1,1]中
而我們生成擾動的方式採用的是numpy.random.noraml()所以必須乘上一個係數,然後clip保證不會出界
epsilon是我們的最大擾動,我們這裡計算擾動採用的是無窮範數,通過epsilon計算出新增擾動以後的上下界
通過上下界再去clip可以保證我們的音訊在擾動後聽起來還和原來的一樣
max_lr和min_lr 是我們的學習速率,我這裡採用的是基於動量的學習率,如下公式
公式中的pre_grad是上一次迭代的梯度估計值,estimate_grad則是本次的迭代估計值
公式為:momentum * pre_grad + (1.0 - momentum) * estimate_grad
adv_sample_nums是生成的擾動音訊的數量,我們將會對這些擾動後的梯度取平均,這個梯度的計算很簡單。就是下面這行。
estimate_grad = np.mean(loss * noise, axis=0, keepdims=True) / sigma
這裡的loss計算為np.maxmium(scores[1st]-scores[2ed],-1*k)
adver_thresh是一個用於控制置信度的引數,這個引數設定的越大,那麼最終得到的置信度就越高
這個引數屬於【0,1)
plateau_length 用於控制 記錄的往期loss 的數量 ,當這個值為5,那麼只會記錄最新的5個loss
plateau_drop 用於修改學習率,這個值越大學習率下降的越快
通過上面兩個值我們就可以控制學習率的大小,當我們對比往期的loss
發現loss變大了,我們就會根據設定的plateau_drop去調整學習率
"""
adver=attack(model=model,label_class=label_class,audio=x,sr=sr,true_index=label_index,
sigma=0.002,max_iter=1000,epsilon=0.005,
max_lr=0.001,min_lr=1e-6,adv_sample_nums=50,
adver_thresh=0,momentum=0.9,plateau_length=5,plateau_drop=2.)
"""
攻擊結束了,讓我們看看我們攻擊後的音訊的波形圖對比
"""
#首先轉換下adver的格式
adver=np.array(adver.tolist()[0])
plt.figure(figsize=(14, 7))
plt.subplot(2,1,1)
librosa.display.waveplot(x, sr=sr)
plt.subplot(2,1,2)
librosa.display.waveplot(adver, sr=sr)
"""
再看看頻譜圖的對比
"""
plt.figure(figsize=(14, 7))
X = librosa.stft(x)
Xdb = librosa.amplitude_to_db(abs(X))
plt.subplot(2,1,1)
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')
X = librosa.stft(adver)
Xdb = librosa.amplitude_to_db(abs(X))
plt.subplot(2,1,2)
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')
下一步的幾個實驗
- 嘗試訓練並攻擊一個使用均值濾波的模型
- 真實世界的攻擊
- 目標攻擊