網路資料的K-means聚類演演算法
隨著Internet的大規模普及、資訊處理技術和資料處理技術的發展及企業資訊化程度的提高,各種網路資源以爆炸式速度迅猛增長,現存的網路資源以資料庫儲存的形式為主,資料的形式以半結構化和結構化的形式儲存。但是在網路技術迅猛發達的今天,資料庫中的資料量更是以驚人的速度發展,就形成了資料量很大而對於有用的資訊的發掘和利用成為一大難題的現象,也成為現在研究的熱點問題。
如何從激增的資料背後找到有價值的資訊,並從中提取出知識己經成為目前資料探勘和知識管理等研究領域的重要課題。而資料探勘技術正是解決這一課題的重要方法。其中聚類(clustering)是資料探勘三大領域(關聯規則,聚類,分類)之一,是分析資料並從中發現有用資訊的一種手段。它將資料物件的集合分組成為由類似的物件組成的多個簇。同一個簇中的物件彼此相似,不同簇中的物件彼此相異。物件間相似度是根據描述物件的屬性來進行計算的。距離是經常採用的度量方式,從機器學習的角度來看,聚類屬於無指導學習,與分類不同,聚類和無指導學習不依賴於預先定義的類和帶標號的類的訓練範例。
聚類分析具有廣泛的應用價值,如市場分割、圖形識別、生物學研究、空間資料分析、web檔案分類。除此之外,聚類分析還可以作為獨立的資料探勘工具,來了解資料釋出,或者作為其他資料探勘演演算法的預處理步驟。
聚類已經被廣泛地研究了許多年,迄今為止,研究人員己經提出了許多聚類演演算法,大體上這些演演算法可以分為基於劃分的方法、基於層次的方法、基於密度的方法、基於網格的方法和基於模型的方法。其中,K-means屬於聚類分析中一種基本的劃分方法,常採用誤差平方和準則函數作為聚類準則。主要優點是演演算法簡單、快速而且能有效地處理巨量資料集。
1.2 國內外研究現狀
現有的聚類演演算法雖然眾多,但它們都或多或少地存在著一些缺陷和不足。迄今為止沒有任何一種聚類演演算法可以對於任何一類資料集,針對任何一種應用要求都能夠達到高品質的聚類效果。目前對聚類演演算法的探討和改進是國內外專家、學者的熱門話題。聚類過程的本質是一個優化的過程,通過一種迭代運算使得系統的目標函數達到一個最優解。
K-均值演演算法是聚類分析中基於劃分方法的一種經典演演算法,思想簡單,效率高,應用領域相當廣泛,比如檔案聚類、圖象分割等應用。K-means演演算法從提出到現在也經歷了一個很長的發展階段,由於其經典性、可應用性強、快速和簡單等特點,人們進行了大量的研究。K-means演演算法的應用主要體現在一下幾個方面:
·K-means演演算法在高維資料中的應用;
·K-means演演算法在流式資料中的應用;
·K-means演演算法在部分資訊資料中的應用;
·K-means演演算法在有偏資料中的應用。
1997年,Mitchell就如何以混合模型演演算法的形式,對基於平方歐幾里德距離的K—均值演演算法進行了研究分析。2000年,Steinbach,Karypis和Kumar提出了二分K—均值演演算法,該演演算法進行對整個資料集進行劃分,知道使用者設定類的個數,該演演算法聚類效果和計算效率都比較好,還一定程度解決了原k-means演演算法選取初始點方法所產生的問題。2002年,Dhillon,Guan和Kogan提出了區域性搜尋策略「first variation」,改進了基於餘弦相似度的K-均值演演算法。2003年,Dhillon等提出了輔助文字分類的文字屬性聚類方法和基於資訊理論的聯合聚類方法,他是從資訊理論的角度對基於KL散度的K-均值演演算法進行研究。由於k-means演演算法對孤立點很敏感,初始點的選擇該演演算法的影響比較大,因此人們近些來在這些方面也做了大量的研究。
k-means演演算法在經過長期的發展過程中,雖然得到了很多的改進,對其缺點和優點人們也進行了大量的研究,本文將重點介紹K-means演演算法,並分析其存在的優缺點,最後提出了一種改進的K-means演演算法。
2.1 聚類分析概述
資料探勘技術出現的時間不長,相應聚類方面的研究時間也不長,但是其發展非常迅速,在工程中的應用,特別是在搜尋引擎中的應用非常廣泛,聚類的理論和技術迅速增加。各種經典聚類演演算法相應出現,在聚類過程中,每種聚類演演算法表現出一定的缺點和侷限性,針對這些問題,人們不斷的對聚類演演算法的再改進,同時提出相應的理論作為改進的基礎。比如提出孤立點的問題,計算樣本間距離的不同計算方法,聚類結果品質的評定等。
K-means演演算法作為一種基於劃分的經典演演算法,開始只是提出了一種聚類過程的思想,當然存在很多缺點和侷限性。從提出到現在的整個發展過程中,人們針對它存在的問題,在原k_means演演算法的基礎上提出了大量的改進演演算法。所有的改進演演算法,大部分都是把其他的聚類方法,比如,基於層次方法、基於密度方法等,應用到K-means的演演算法步驟當中,而改進之後,也只是解決某一方面的問題。
現在隨著網路使用者的快速增加,資料資訊的膨脹速度更是驚人,那麼在聚類過程中對巨量資料量的聚類效果和時間也成為聚類研究非常關心的問題,人們也提出了一些解決辦法,但是真正解決還需時間。針對K-means演演算法,改進之後會出現使用者輸入引數增加,聚類資料形狀要求嚴格等問題現在一直沒有得到很好的解決。而最關鍵的使用者輸入引數直接影響聚類的效果,如何解決這一問題,還需要進一步研究。
聚類分析是資料探勘的一個重要領域,而聚類演演算法是研究的核心。聚類是將沒有類別標記的物件,根據其特徵,將其劃分為不同的資料類。目的是使得屬於同一類別的個體之間的距離儘可能的小(很高的相似度),而不同類別上的個體間的距離儘可能的大(相似度儘可能的小)。聚類方法包括統計、機器學習方法、神經網路方法和麵向資料庫的方法。
傳統K-means聚類演演算法概述
根據K-means演演算法的基本流程,這裡將對傳統的K-means演演算法做簡單的模擬,這裡,模擬所使用的資料為一組空間座標點,其座標點的分佈如下圖所示:
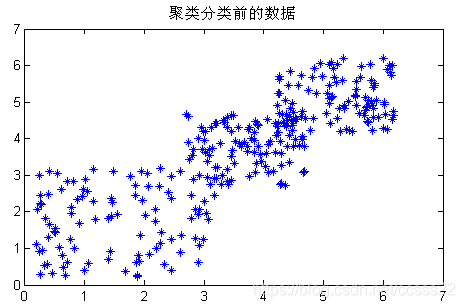
圖3.2 初始化產生的資料分佈1
這裡,初始化的資料由預先設定的三組資料組成,即初始化的資料集聚類如下圖所示:
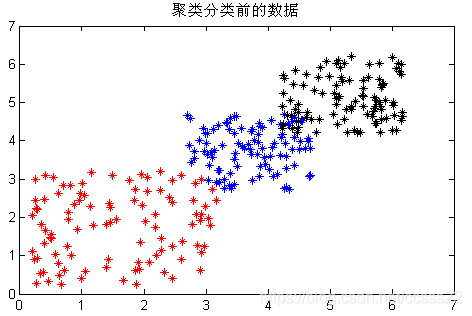
圖3.3 初始化產生的資料分佈2
然後,我們將這組資料輸入到K-means演演算法進行聚類分析,得到的分類結果如下所示:
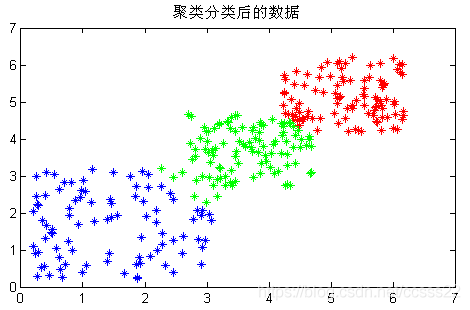
圖3.4 聚類分析之後的資料集
從圖3.4的模擬結果可知,初始的亂數基本能夠正確的分成了3類,和初始化輸入的資料種類相似。每一類的識別率達到了80%左右。
一般而言,K-均值聚類演演算法存在的主要問題有以下幾個方面:
·K-均值聚類演演算法中聚類個數k需要被預先給定。聚類個數k值的選定是很難估計的,很多的時候,我們事先並不知道給定的資料集應該分成多少類才最合適。
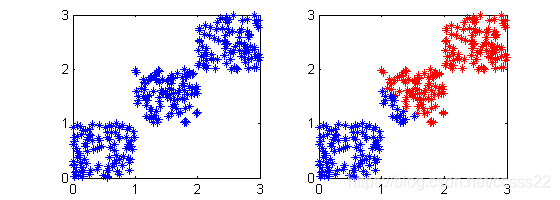
圖3.5 K值不確定時的錯誤聚類
如圖3.5所示,假設有三類資料,但是當K值無法確定的時候,假設取K值為2,那麼其聚類結果則如圖3.5右圖一樣,顯然,這種聚類結果並不是最佳的聚類結果,因此K值的確定,對聚類結果有著較大的影響。
·演演算法對初始值的選取依賴性極大以及演演算法常陷入區域性極小解。K-均值演演算法首先隨機地選取k個點作為初始聚類中心,再利用迭代的重定位技術尋找最優聚類中心直到演演算法收斂。因此,初始值的不同可能導致演演算法聚類效果的不穩定。
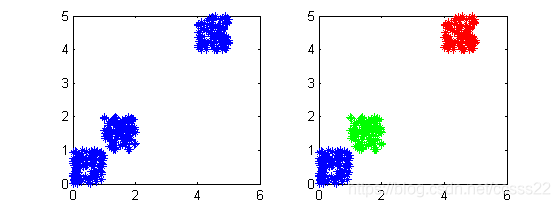
(a).初始聚類中心點1

(b).初始聚類中心點2
圖3.6 不同初始聚類中心點的聚類分析結果
如圖3.6所示,對於不同的聚類中心點的選取,會導致最後的聚類結果的不同。
·將簇的質心作為聚類中心進行新一輪聚類計算,將導致遠離資料密集區的孤立點和噪聲點會導致聚類中心偏離真正的資料密集區,所以K-均值演演算法對噪聲點和孤立點非常敏感。
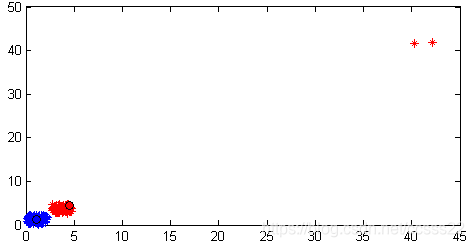
圖3.7 孤點對聚類中心的影響
從圖3.7的模擬結果可知,如果存在孤點的時候,會對實際的聚類中心點有較大的影響,如上圖紅色資料的中心點。
·對於巨量資料量,演演算法的開銷非常大。從K-均值聚類演演算法流程可以看出,該演演算法需要不斷地進行樣本分類迭代調整,不斷地計算調整後的新的聚類中心。因此,當資料集的數量非常大時,演演算法的時間開銷也是相當驚人的的。所以需要對演演算法的時間複雜度進行分析,改進,
以提高演演算法的應用範圍。
根據前一章提出的改進辦法,本章將重點使用改進後的演演算法資料進行模擬並對比改進前後的K-means演演算法的聚類結果。
人為模擬產生3類混合資料來源作為測試源,測試結果如下所示:

圖3.8 去孤點模擬
從圖3.8可知,通過改進後的K-means演演算法,可以有效去除一些比較明顯的孤點,從而大大增加了聚類中心值。
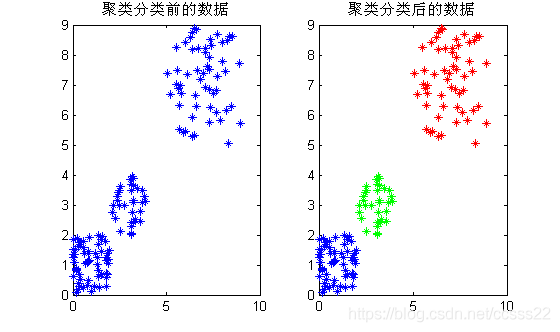
圖3.9 未設定K=3,軟體自動識別最佳類別為3
圖3.9可知,在沒有預先設定K的情況下,通過改進後的K-means演演算法,可以自動識別到最佳的類別數為3,在MATLAB的命令視窗可以看到具體的執行結果:

人為模擬產生4類混合資料來源作為測試源,測試結果如下所示:
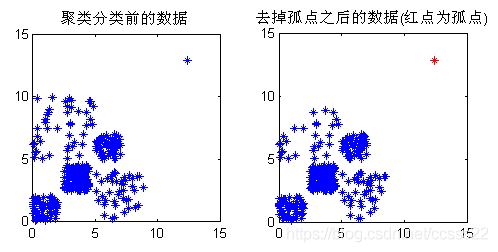
圖3.10 去孤點模擬
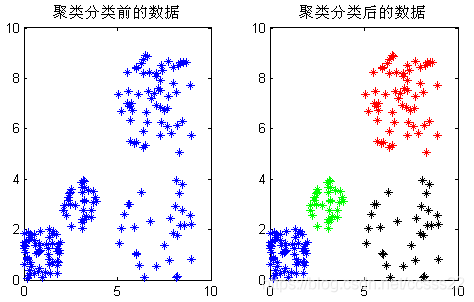
圖3.11 未設定K=4,軟體自動識別最佳類別為4
圖3.11可知,在沒有預先設定K的情況下,通過改進後的K-means演演算法,可以自動識別到最佳的類別數為4,在MATLAB的命令視窗可以看到具體的執行結果:

人為模擬產生5類混合資料來源作為測試源,測試結果如下所示:

圖3.12 去孤點模擬

圖3.13 未設定K=5,軟體自動識別最佳類別為5
圖3.13可知,在沒有預先設定K的情況下,通過改進後的K-means演演算法,可以自動識別到最佳的類別數為5,在MATLAB的命令視窗可以看到具體的執行結果:

第四章 基於K-means演演算法的網路資料的聚類分析
本章,我們將應用第三章的研究成果,使用改進後的K-means演演算法對網路使用者資料資訊進行聚類分析,本課題,重點對網路資料中的使用者工作地點等相關資料進行提取和聚類分析,進而將分析出哪些客戶在哪些區域工作或者經常在哪些區域活動。
4.1 網路資料的獲得與分析
這裡,從網站「http://reality.media.mit.edu/download.php」下載「the Reality Mining project」的資料庫,用作本課題的實際的測試資料,使用MATLAB進行價值,可以看到如下的資料資訊:
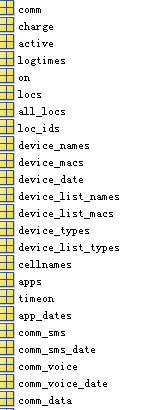
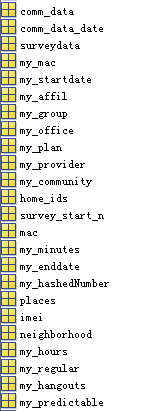

圖4.1 網路資料列表
根據本課題的要求,我們需要通過該資料庫進行分析,從而提供各種網路資料服務,比如使用者工作的地點的分析,使用者登入時間的分析,使用者使用電腦裝置類別,使用者傳送簡訊資訊等等。
這裡我們將重點根據資料庫中的地址資訊來分析不同使用者的實際工作地點或者活動地點。
4.2 測試樣本的提取
本文,將針對使用者工作地點的相關資訊進行聚類分析,獲得使用者的工作地址聚類結果。下面將對資料進行提取,獲得初始的測試資料集。
4.2.1 測試樣本的選擇
通常情況下,我們可以根據每個人的生活特點,將一個人的特性歸納為如下幾點:
表4.1 使用者特性分類表
| 分類 | 說明 | 評價 |
| 按使用行為細分 | 按使用者使用量高低區隔隔優勢; | 方法簡單、固定,容易進行定量分析; |
| 按人口統計學/地理學細分 | 按使用者社會等級區隔; 按使用者性別、年齡、職業區隔 按城區、鄉鎮等區隔 | 方法簡單、固定,容易進行定量分析; |
測試資料子集合的選取,根據課題的研究需要,我們選擇資料庫中的locs,all_locs,loc_id作為測試樣本資料。此外,選擇my_office,my_group作為使用者工作地點的聚類分析資料來源,最後選擇my_mac作為使用者使用電腦的MAC實體地址的聚類分析資料來源。
通過上面的選擇,我們可以通過聚類分析獲得如下的聚類結果:
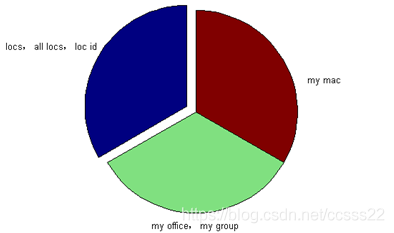
圖4.2 資料選擇圖
最後,從提取的資料中可以知,my_mac,my_office,my_group等三組資料其具有唯一性和可分辨性,即通過數值本身即可得知該使用者的相關資訊,因此,這裡不需要進行進一步的聚類分析,所以,最後我們只對locs,all_locs,loc_id等三組資料進行資料 提取和例外處理。
locs中的資料的含義為:通訊時間,地區標號.通訊小區標號;
All_locs中的資料的含義為:地區標號.通訊小區標號;
Loc_ids中的資料的含義為:locs資料的中索引值,即基站ID號;
因此,在本質,我們所用到的資料為通訊時間,基站ID號,地區標號,通訊小區標號,所以,最後只需要將這四組資料進行提取分析。
4.2.2 資料的提取和異常資料的排除
在為每一個使用者生成所有的變數後,必須對資料進行清洗,檢查所有變數的缺失值、未知值、無效值或有效值。
缺失值:一條記錄(觀測)的某個欄位(變數)沒有值,為空;
未知值:一條記錄(觀測)的某個欄位(變數)有值,但不知道其意義;
無效值:一條記錄(觀測)的某個欄位(變數)值是無效的,但其意義是已知的;
有效值:一條記錄(觀測)的某個欄位(變數)值是有效的,這是正常的情況。
資料淨化的過程就是把缺失值、未知值或無效值用有效值替代的過程。經過檢查本研究資料有大量缺失值的發生,因為某些客戶在某些特定的產品沒有進行交易,因此在不同的表關聯到一起的時候有缺失的情況發生,對這部分記錄全用0代替。沒有未知值和無效值的情況發生。
此外,對於資料的異常值,本文采取的措施是刪除,最後,為了提高聚類的效果,需要去掉相關性較高的變數,主成分分析可以生成原始變數線性組合的主成分,這些主成分既保留了原始變數的大部分資訊,而且相互獨立,可以提高聚類的效果。本研究對相關性較高的變數提取主成分,這些主成分和與任何變數都不相關的變數一起作為聚類的輸入變數。
通過上面的操作之後,將所需要的資料單獨儲存為*.mat格式,這樣可以方便的為後面的操作使用。
在MATLAB中,執行「data_catch.m「程式碼執行資料提取和儲存。此時,我們將所用到的資料資訊通訊時間,基站ID號,地區標號,通訊小區標號儲存到了其他資料庫中:
最後考慮資料的唯一性,即為了對不同區域的使用者進行聚類分析,那麼不考慮時間因素,這樣可以只儲存每個使用者出現過的活動區域,從而方便最終的聚類分析。
這樣,在後期的處理的時候,可以大大提高資料處理效率。
4.3 基於K-means演演算法的樣本聚類分析
4.3.1 將測試樣本資料應用到K-means演演算法之中
用K-Means演演算法進行聚類分析,最重要的兩個引數是最大類的個數K以及K個初始凝聚點的選擇。本文所設計的K-means演演算法將對K值進行自動搜尋,獲得最佳的K值,而初始化聚類中心,則採用隨機設定的辦法進行。
在資料輸入到K-means演演算法之前,為了便於觀察分類的結果,將資料中的areaID作為實際測試資料的X軸座標,將cellID作為實際測試資料的Y軸座標,那麼如果兩個測試點重合,這說明兩個使用者處於同一地點,如果X軸相同,而Y不相同,那麼說明兩個使用者在同一地點,但是出於不同的通訊小區,如果X軸不同,而Y軸值相同,那麼說明兩個使用者在不同的地區,但是在相同的小區。
由於,網路資料庫的資料量非常大,無法直接進行處理,這裡,我們採取的措施為選擇每個使用者出現最多的幾個區域area和小區cell作為處理樣本進行聚類分析。這樣做的優勢在於,在資料量非常大的時候,通過選取出現概率最大的幾組資料作為代表性資料,能夠最大程度上反映資料的實際特徵。
這裡,考慮實際情況,選取出現概率最多的六組資料作為測試資料。
通過MATLAB模擬,測試資料可以表現出如下的結果,即每個使用者的大致分佈。
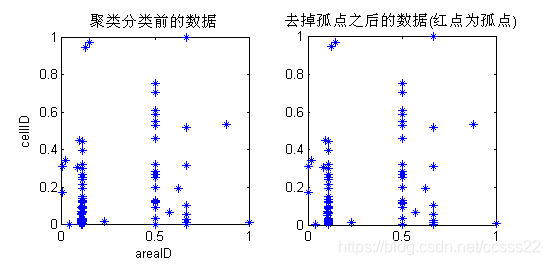
圖4.3每組出現最多的一組AreaID分佈圖
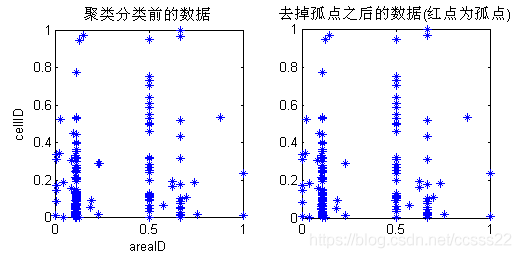
圖4.4每組出現最多的二組AreaID分佈圖
從圖4.4可知,使用者的區域ID主要集中在兩個區域,這類似於實際中的工作地點和家庭住址,而其餘比較散的點對應著其餘較少活動的場所。
從上面的模擬可知,由於使用者分佈具有較大的隨機性,且對於各個使用者而言,其基本會出現經常去的地方,或者是很少去的地方,那麼對於這些較少出現的區域,可以認為是取樣資料中孤點進行處理。
4.3.2 將測試樣本資料應用到K-means演演算法之中
我們將測試樣本輸入到改進後的K-means算中,進行模擬。
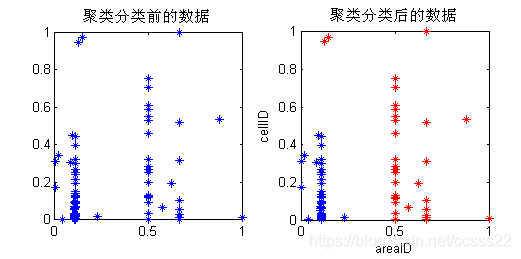
圖4.5每組出現最多的一組AreaID的聚類分析結果
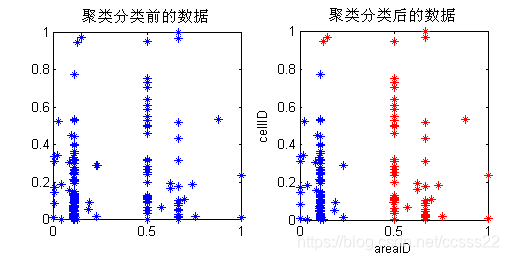
圖4.6每組出現最多的二組AreaID的聚類分析結果
從上面的聚類模擬結果可知,系統自動將使用者所在的區域聚類成兩大類,這個和前面所考慮的兩類場所的實際情況向吻合。