「 客星璀璨之夜 」（stars）

「

    雖然不清楚是不是那兩人的力量

    在那個風暴肆虐的夜晚，的確有一瞬

    真的在那一瞬間，在雲破天開的時候

    透過空隙中看到的璀璨星空，不知為何倒映眼中不能忘懷 

」

                    ——《奇蹟召喚星辰》

【題目描述】

       小苗望著星空，在高中學習了幾年物理後正式成為一名理科生後，她突然腦洞大開： 將星空簡化成一個數軸，數軸上有 2n + 1 個位置，分別為 x_1 , x_2 , … , x_2n+1，其中奇 數位置有一個正物質恆星，偶數位置有一顆反物質行星。在這裡，我們不考慮天體之間 力的作用。

       小苗將發動奇蹟的力量，從剩下的反物質行星中隨機選擇一顆，並隨機選擇向左或 向右，然後施加一個初速度。顯然，當正物質與反物質相撞後，它們會發生湮滅並同時 消失。

       當上一個行星湮滅後，小苗會再次發動奇蹟的力量，直到不存在行星。可以注意到， 沒有行星會永遠運動下去。 小苗除了學習了物理外，還學習了概率論，所以她想知道所有行星在湮滅之前的運 動距離之和的期望為多少。但是這對於周老師實在是太難了，所以小苗決定向你求助。 你只需要算出期望值 mod 998244353 的結果。

       p.s.：如果你不知道模意義下的期望怎麼求，首先期望一定能寫成有理數 a/b，在 mod 998244353 意義下存在唯一正整數 b^−1 滿足 b × b^−1 ≡ 1 mod 998244353，你只 需要輸出 a × b^−1 mod 998244353 的值即可。

【輸入格式】

從檔案 stars.in 中讀入資料。

第一行包含一個正整數 n。接下來一行共 2n + 1 個整數 x_1 , x_2 , … , x_2n+1 表示所有天 體的座標。保證 xi 遞增給出。

【輸出格式】

輸出到檔案 stars.out 中。

輸出期望值 mod 998244353 的結果。

【樣例 1 輸入】

1

1 2 3

【樣例 1 輸出】

1

【樣例 2 輸入】

3

1 2 3 4 5 6 7

【樣例 2 輸出】

332748122

【樣例 2 解釋】

共存在 3! × 2^3 = 48 種不同的可能性，限於篇幅不列舉所有情況，期望值為 13/3 。

【樣例 3 輸入】

10

0 1 3 6 10 15 21 28 36 45 55 66 78 91 105 120 136 153 171 190 210

【樣例 3 輸出】

969129126

【資料範圍與約束】

對於所有測試點，滿足 n ≤ 3000, −10^9 ≤ x_1 < x_2 < ⋯ < x_2n+1 ≤ 10^9。

題解

我們把題意轉換一下，相當於每次隨機把相鄰兩顆星球（一正一反）並在一起湮滅，消失，旁邊的兩顆星球變為相鄰。

每個行星都會唯一地運動一段距離，顯然每個行星都有概率與n+1顆恆星湮滅，也就是每個行星有n+1種情況，n+1種概率，總的就有n(n+1)種情況，可以直接列舉，複雜度為n^2，只要算出當前行星與每一顆恆星湮滅的概率，再分別乘對應的移動距離，加起來就是總期望了。

假如我們要讓左數第 i 個行星與左數第 j 顆恆星相撞，這個概率怎麼算 ？

j 在左邊或在右邊肯定是兩種情況，但本質是一樣的，概率和距離、方向無關。

那麼得滿足幾個條件，

1. i 朝著 j 的方向合併 （p = 1/2）
2. i ~ j 之間的所有星球得在 i 之前湮滅掉，並且不影響到 j （p = ?）
3. i → j 方向更遠處的星球不能影響到 j ，但可以不在 i 之前湮滅 （p = ?）

分別考慮一下2和3吧

條件2

下圖的黑點是反物質行星，白點是恆星

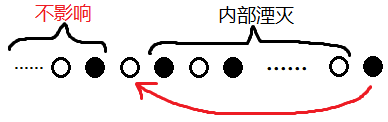
設內部湮滅的中間點總共有 L 對，那麼顯然他們內部湮滅的概率只跟 L 大小有關，跟距離、位置、甚至方向都無關，

所以設 dp1[i] 為長度為 2i （即中間有 i 對）的連續一段星球互相湮滅的概率（為了不重複考慮，dp1就只要求自己內部不影響外面，而暫不考慮外面對自己的影響），

再設 dp0[i] 為長度為 2i 的連續一段星球互相湮滅，且最外面兩個星球最後相撞的概率，

 

（乘二分之一是因為最外面的那個行星得朝內，乘 i 分之一是因為最外面那個行星得是 i 個行星中最後移動的）

那麼簡單想一下會發現如下轉移：

簡單解釋一下為什麼那裡是dp0而不是dp1，

如果是dp1的話，首先他會算重，然後是需要加上自己，會出問題，

列舉 j 實際上是列舉第一個dp0的長度。

好了，我們繼續看上面的三個條件，發現前兩個條件可以合併一下，用一個包含 i，j 的 dp0 表示，dp1，dp0都可以 n^2 預處理

條件3

這個就比較麻煩了，可以允許兩種情況

第一種情況就直接是dp1[j-1]，很簡單

第二種情況是筆者做法的重難點，咱們慢慢來

重難點

首先需要強調的是，其中任意一個行星都可以選擇在 i 合併之後再出去合併，這樣的話，假設該行星為 k 

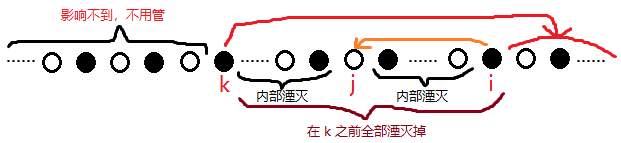
我們發現這個概率居然和 i~k 的總長度有關，而對於每個不同的 k ，i~k 的長度又不一樣，那是不是要n^3了呢？

不，絕對不能n^3，

我們發現如果設 dp2[x][y] 為上圖 i~j 長度為 2x 、j~k 長度為 2y 時滿足 k 最後的概率，那麼 dp2 可以 O(1) 轉移，

然後預處理一下 dp2[i][1]~dp2[i][j]的字首和，就可以直接帶入了。

本來dp2是要乘那個dp0[i]的，至於轉移方程中為什麼要打上一個括號，是為了總計算方便，筆者的程式碼裡沒有乘它。

複雜度

所有dp都可以預處理，都是n^2，列舉也是n^2的，總複雜度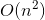

CODE

#include<cstdio> 
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 6010
#define LL long long
#define DB double
#define ENDL putchar('\n')
//#define int LL
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x = x*10+(s-'0');s = getchar();}
	return f * x;
}
const int jzm = 998244353;
int n,m,i,j,s,o,k,a,b;
int fac[MAXN],inv[MAXN],invf[MAXN],pow2[MAXN],inv2[MAXN];
int C(int n,int m) {return fac[n] *1ll* invf[n-m] % jzm *1ll* invf[m] % jzm;}
int ad[MAXN];
int dp[MAXN],dp0[MAXN],dpr[MAXN>>1][MAXN>>1];//dp1,dp0,dp2/dp0[i] 
int main() {
	freopen("stars.in","r",stdin);
	freopen("stars.out","w",stdout);
	n = read();
	pow2[1] = 2;inv2[0] = 1;inv2[1] = 499122177;
	fac[0] = fac[1] = inv[0] = inv[1] = invf[0] = invf[1] = pow2[0] = 1;
	for(int i = 2;i <= (n<<1|1) || i <= 10;i ++) {
		fac[i] = fac[i-1] *1ll* i % jzm;
		inv[i] = (jzm - inv[jzm % i]) *1ll* (jzm / i) % jzm;
		invf[i] = invf[i-1] *1ll* inv[i] % jzm;
		pow2[i] = pow2[i-1] *2ll % jzm;
		inv2[i] = inv2[i-1] *1ll* inv2[1] % jzm;
	}
	dp0[0] = dp[0] = 1;
	for(int i = 1;i <= n;i ++) {
		dp0[i] = dp[i-1] *1ll* inv[i] % jzm *1ll* inv2[1] % jzm;
		dp[i] = dp0[i];
		for(int j = 1;j < i;j ++) {
			(dp[i] += dp[j] *1ll* dp0[i-j] % jzm) %= jzm;
		}
	}
	// !!!必須先處理了dp0和dp1才能處理dp2!!!
	for(int i = 1;i <= n;i ++) {
		for(int j = 1;j+i <= n;j ++) {
			dpr[i][j] = dp[j-1] % jzm *1ll* inv2[1] % jzm *1ll* inv[i+j] % jzm;//由於下面計算概率時乘了個dp0[i]的 ,所以這裡不用乘dp0[i] 
			(dpr[i][j] += dpr[i][j-1]) %= jzm;
		}
	}
	// 預處理結束 ，可能處理了一些多餘的，不過沒關係 
	for(int i = 1;i <= (n<<1|1);i ++) {
		ad[i] = read();
	}
	// 輸入結束 
	int tot = fac[n] *1ll* pow2[n] % jzm; //方便偵錯而已，並沒用 
	int ans = 0;
	for(int i = 1;i <= n;i ++) {
		for(int j = 1;j <= i;j ++) {
			int p = dp0[i-j+1] *1ll* ((dp[j-1] + dpr[i-j+1][j-1]) % jzm) % jzm;
			(ans += (ad[i<<1] - ad[(j<<1)-1]) % jzm *1ll* p % jzm) %= jzm;
//			printf("(%d -> %d) : %d\n",i,j,p);
		}
		for(int j = i+1;j <= n+1;j ++) {
			int p = dp0[j-i] *1ll* ((dp[n+1-j] + dpr[j-i][n+1-j]) % jzm) % jzm;
			(ans += (ad[(j<<1)-1] - ad[i<<1]) % jzm *1ll* p % jzm) %= jzm;
//			printf("(%d -> %d) : %d\n",i,j,p);
		}
	}
	printf("%d\n",ans);
	return 0;
}