【初賽】初賽提綱（to be countinue）

前言：

快初賽了，以防萬一，整理了一些知識點

1.計算機發展代別劃分

代別	年代	邏輯（電子）元件
第一代	1946 - 1958	電子管
第二代	1959 - 1964	電晶體
第三代	1965 - 1970	積體電路
第四代	1971 - 至今	（超）大規模積體電路

2.計算機硬體裝置

由 記憶體、運算器、控制器、輸入裝置、輸出裝置 構成

記憶體：顧名思義就是用來存東西的可以分為兩大類。

主記憶體（記憶體）	輔存（外存）
與CPU地址線直接相連的記憶體就是記憶體	通過介面與CPU間接相連的記憶體就是外存

運算器：運算器由算術邏輯單元（ALU）、累加器、狀態暫存器、通用暫存器組等組成。算術邏輯運算單元（ALU）的基本功能為加、減、乘、除四則運算，與、或、非、互斥或等邏輯操作，以及移位、求補等操作。

控制器：計算機的指揮系統。

輸入裝置：比如：鍵盤、滑鼠、掃描器、麥克風之類的。
輸出裝置：比如：顯示器、印表機、音箱之類的

3.進位制之間的轉換

二進位制：逢二進一
八進位制：逢八進一
十進位制：逢十進一
十六進位制：逢十六進一不同的是，用ABCDEF代表10、11、12、13、14、15、

二進位制轉十進位制方法：「按權展開求和」
比如將 $1011.10）^{2}$ 轉成十進位制數

（ $1$ * $2^3$ + $0$ * $2^2$ + $1$ * $2^1$ + $1$ * $2^0$ + $1$ * $2^ {-1}$ + $0$ * $2^{-2}$ ）

（ $2^{-n}$ = $\frac{1}{2^n}$ )(n >= 0) 例如( $2^{-1}$ = $\frac{1}{2^1}$ ）

$（ 8 + 0 + 2 + 1 + 0.5 + 0 ）$ = $11.5)^{10}$

十進位制轉二進位制方法：「除以2取餘數然後逆序輸出」
比如將 $89）^{10}$ 轉成二進位制數

  2  |89
     ————
  2  |44      ....... 1
     ____
  2  |22      ....... 0
     ————
  2  |11      ....... 0
     ____
  2  |5       ....... 1
     ————
  2  |2       ....... 1
     _____
  2  |1       ....... 0
     _____
     0        ....... 1

然後倒著念就是 $1011001)^{2}$

4.資訊編碼表示

1.編碼：將各類資訊轉換成0和1，即二進位制數，這一過程稱為編碼
2.資料：能被計算機接受和處理的符號的集合稱為資料
3.位元：指1位二進位制的數碼（0 或 1）。位元是計算機中表示資訊的資料編碼中的最小單位
4.位元組：位元組表示一組連續二進位制數。通常用8位元2進位制數表一個位元組，也就是1位元組=8位元
5.ASCLL碼：
0 ~ 9 —— 48 ~ 57
A ~ Z —— 65 ~ 91
a ~ z —— 97 ~ 123

5.關於各種排序

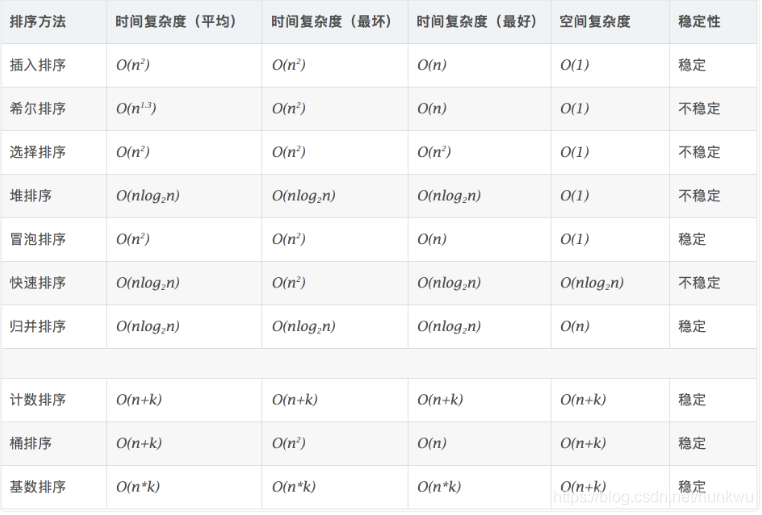
在這裡插入圖片描述

6.計算機網路：

1.網路的定義：利用通訊線路和裝置，把分佈在不同地理位置上的多臺計算機連線起來。
2.網路的分類：

區域網（LAN）	一般侷限1km範圍內，區域網傳輸速率較高，誤位元速率低，結構簡單、容易實現
都會網路(MAN)	一般範圍為幾km到幾十km以內
廣域網(WAN)	一般範圍幾十km到幾千km

3.IP地址：
用於標識Internet網路上節點的32位元地址。
該地址通常由句點分隔的八位位元組的十進位制數表示（例如：192.168.7.27）
IP地址的主機號的每個域取值範圍0~255，但主機ID所有域不能都為0或255.

7.原碼二補數反碼

原碼：
第一位代表符號位0為正，1為負
然後接他的二進位制數
設x=11110001 則x原 = 011110001

反碼：
正數的反碼就是他的原碼
負數的反碼就是除了符號位（第一位）以外的數全都取反
例如1111010 的反碼就是 1000101

二補數：
正數的二補數就是他的原碼
負數的二補數符號位為1，數值各位取反，最低位+1

8.邏輯運算

非：！
與：&
或：|
互斥或：^

運算級比較
括號>非>與>或和互斥或

非：0變1,1變0；簡單記憶就是取反
與：有1為假必為假簡單來說就是隻要有0就是0兩個1才是1
或：有1為真必為真簡單來說就是隻要有1就是1兩個0才是0
互斥或：相同為0不同為1

9.棧

先進後出
例如：
入棧順序：1 3 2 4 5
出棧順序：5 4 2 3 1
可以這樣理解棧~~有口無肛門~~ = 嘔吐

10.佇列

先進先出
例如：
入隊順序：8 7 5 6 1 2 3
出隊順序：8 7 5 6 1 2 3
可以這樣理解佇列~~有口有肛門~~ = ~~拉米巴米巴~~

11.樹

1.定義：
每個元素稱為節點
有一個特定的節點，稱為根節點

2.基本概念：
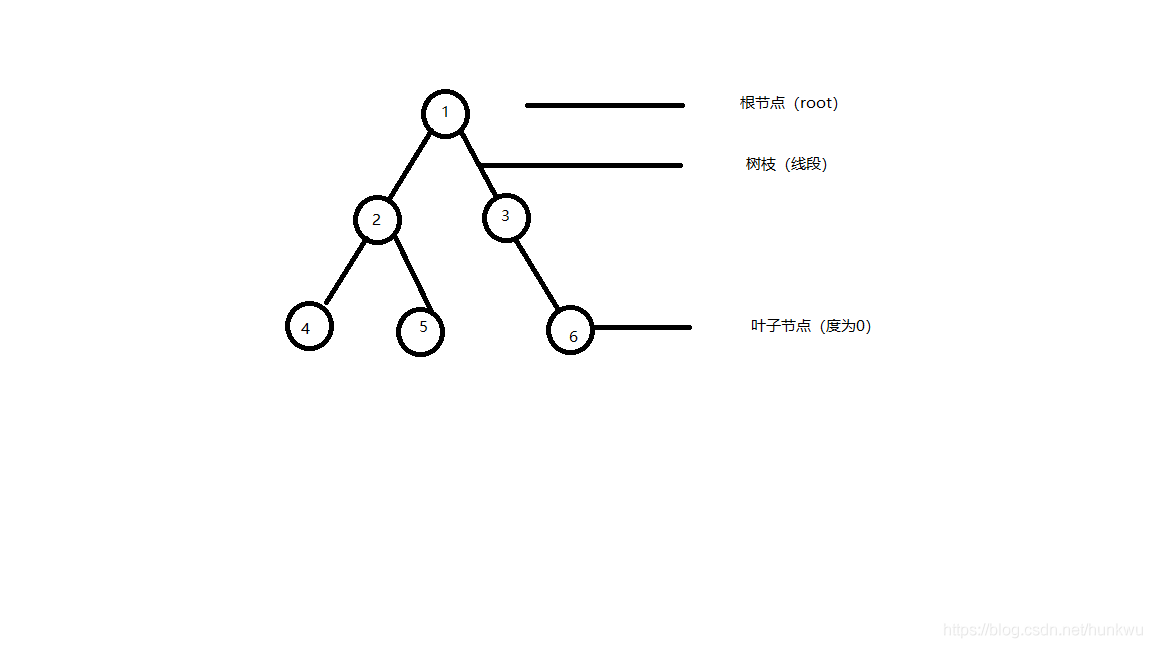
在這裡插入圖片描述
就比如這張圖
節點1是根節點
這棵樹的深度為3
度：一個節點的兒子個數。
葉節點：度數為0的節點，例如節點4 5 6。

3 .樹的遍歷：
先序遍歷：根左右拿上圖說就是123456
中序遍歷：左根右拿上圖說就是425136
後序遍歷：左右根拿上圖說就是452631

4 .二元樹的基本結構：
是一種度數為2的數，每個節點的子節點分別稱為左孩子，右孩子，它的兩顆子樹分別稱為左子樹，右子樹。
二元樹可以為空，一定是有序的

5.二元樹的性質：
在二元樹的第i層有 $2^{i-1}$ 個節點（i>=1）
深度為k的二元樹至多有 $2^{k-1}$ 個節點（k>=1）

6 .特殊的二元樹：
1.滿二元樹：深度為k且有 $2^{k-1}$ 個節點
2.完全二元樹：如果二元樹的深度為k，則除第k層外其餘所有層節點的度都為2，且葉子節點從左到右依次存在。也即是，將滿二元樹的最後一層從左到右依次刪除若干節點就得到完全二元樹。滿二元樹是一棵特殊的完全二元樹，但完全二元樹不一定是滿二元樹

12.圖

1.什麼是圖？：
一種資料結構，定義為G = （V,E）

2.圖的一些定義和概念：
1）：有向圖:圖的邊有方向（箭頭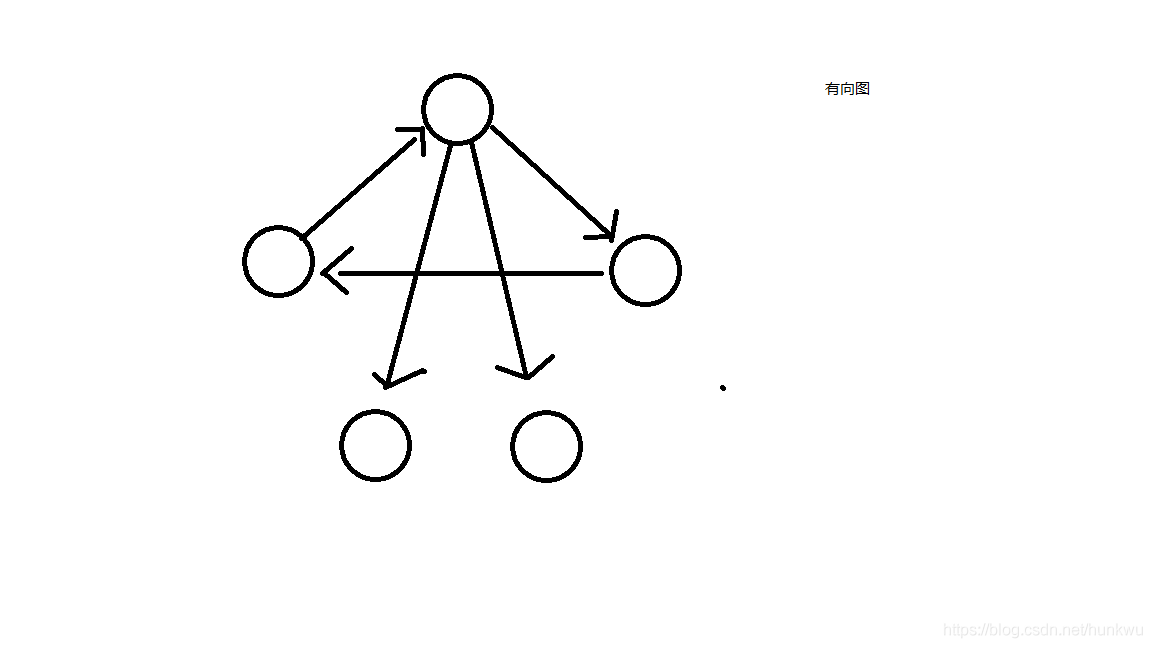）在這裡插入圖片描述

2）：無向圖:圖的邊沒有方向（雙向）
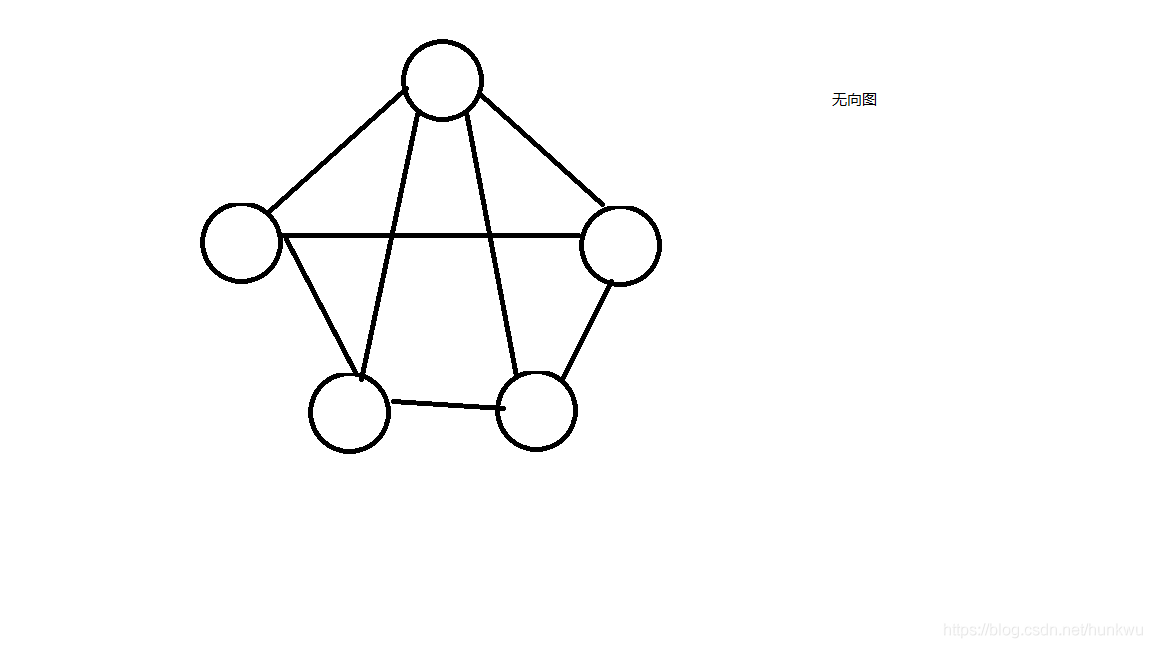
在這裡插入圖片描述
3）：結點的度：無向圖中與節點相連的邊的數量，稱為結點的度。
4）：結點的入度：有向圖中，以某個結點為終點的有向邊的數量。
5）：結點的出度：有向圖中，以某個結點為起點的有向邊的數量。
6）：權值：邊的「費用」，可以理解為邊的長度。
7）：連通：如果圖中結點U,V之間存在一條從U通過若干條邊或點到達V的通路，則稱為UV連通。
8）：迴路：起點和終點相同的路徑稱為迴路或環。
9）：完全圖：
10）：強連通分量

13 物件導向程式設計語言

Smalltalk，Eiffel, C++,java,PHP，C#
C是程式導向程式設計語言
程式導向程式才是「自頂向下，逐步求精」，而物件導向程式設計並不是，而是基於問題物件的自底向上的設計方法。
（就是物件是下到上，過程是上到下）