【人工智慧】從梯度下降演演算法到人工神經網路
提到人工智慧演演算法,人工神經網路(ANN)是一個繞不過去的話題。但是對於新手,往往容易被ANN中一堆複雜的概念公式搞得頭大,最後只能做到感性的認識,而無法深入的理解。正好最近筆者本人也在經歷這個痛苦的過程,本著真理越辯越明的態度,索性坐下來認真的把這些頭大的問題梳理一番,試試看能不能搞清楚ANN背後的數學原理。
其實ANN 的流程概括來說倒不是很複雜,以最簡單的前饋神經網路為例,無非就是
搭建網路架構 ---> 通過比較輸出與標籤的差值構建損失函數的框架 ---> [給出一個訓練樣例(包括ANN的輸入值和輸出值) ---> 得到損失函數 ---> 隨機給出一組初始引數 ---> [ 利用梯度下降演演算法從後往前調整網路引數(誤差反向傳播,BP)] ] ---> 得到所有引數值 ---> 得到ANN並使用
其中大括號 [] 裡的內容是需要反覆迭代的(注意有一部分是雙重回圈)。
在ANN的一堆操作裡,梯度下降演演算法是一個相對獨立的過程,不妨就讓我們從梯度下降演演算法開始吧。
一、梯度下降到底在幹什麼
其實這個問題非常簡單,只是大家被梯度下降複雜的過程搞蒙了,忘記了它的本質。梯度下降演演算法自始至終都在幹一件事——就是找到函數的極值點,當然確切的說是極小值點。但是,這種方法不同於以往我們在高等數學裡學到的找極值點的方法。那麼我們首先就要問,求極值的經典方法不香嗎?
1.求極值:傳統的方法不香嗎?
要回答這個問題,讓我們先快速回顧一下在中學和大學裡學到的傳統的求極值點的方法。
對於一元函數來說,極值可能出現在一階導函數為0的點(駐點)或是導數不存在的點。
例如要找到 f(x) = x^2 + 3x 的極值點
求導得 dy/dx = 2x + 3
令 dy/dx = 0
就得到 x = -1.5 時,導函數為0。
注意,上面找到的只是可能的極值點,也就是極值存在的必要條件。還需要驗證一下充分條件,才能確定極值。這時,可以判斷二階導的正負性、或是判定一階導在可能的極值點兩邊的正負情況。回到我們的例子
當 x < -1.5 時,2x + 3 < 0
當 x > -1.5 時,2x + 3 > 0
說明函數在x = -1.5 附近先下降、後上升
該點是一個極小值點對於二元函數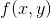 ,情況更復雜一些。首先要找出該函數的駐點和偏導數不存在的點,這些點仍然只是可能的極值點。而二元函數的駐點需要同時滿足兩個偏導數為0的條件,即
,情況更復雜一些。首先要找出該函數的駐點和偏導數不存在的點,這些點仍然只是可能的極值點。而二元函數的駐點需要同時滿足兩個偏導數為0的條件,即
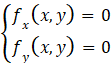
顯然,這裡的駐點是需要解這樣一個二元方程才能求得的。對於駐點分別求出其3個二階偏導數的值,再根據一些規則才能判斷是不是極值點。
還需注意這個判斷規則是不同於一元函數的,因為一元函數極值的充分條件只需要考察一個二階偏導數,而這裡則需要綜合考察二元函數的3個二階偏導數,計算量明顯增大了。對於偏導數不存在的情形還需要特判。
綜合以上,我們可以看出使用經典方法雖然能準確的解出極值點,但當函數自變數的個數很多時,用這種方法求解極值點還真的不香。比如:
- 該方法方法不具有普適性。所謂普適性,就是不能簡單的向多元推廣。從一元到二元的例子可以看出,函數的自變數個數每增加一元,就要研究新的求解方案。可以想象如果是三元函數,其二階偏導數的個數更多,則判斷極值的充分條件還要來的更加複雜。而ANN中可能會求解上億元函數的極值點。
- 其次,這種方法需要解多元方程組,而且這些方程還不一定都是線性的。對於這種多元的非線性方程組,我們的直觀感受就是很難解出。事實上,雖然存在一些可供程式設計的數值計算解法,但計算量大,且求出的是近似解,具有一定的侷限性。
基於此,為了找出多元函數的極值點,我們還需另尋他法。這種方法要簡單易行,特別是要能簡單的向任意元函數推廣,而且這種方法要能夠適應計算機數值計算的特點,畢竟我們這套程式肯定是要放在電腦上跑的。而這就是傳說中的梯度下降演演算法。
2.什麼是梯度?
梯度的概念其實也不難,但為了讓儘可能多的人明白這一概念,我們還是從一元函數開始吧。不過現在我們的目標是——用純粹數值計算的方法,從函數上的某一點出發,找到函數的極值。這裡我們只考察極小值。
2.1一元函數找極值:從列舉試探法到梯度下降法
以函數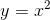 為例,讓我們看看如何找到極值。
為例,讓我們看看如何找到極值。
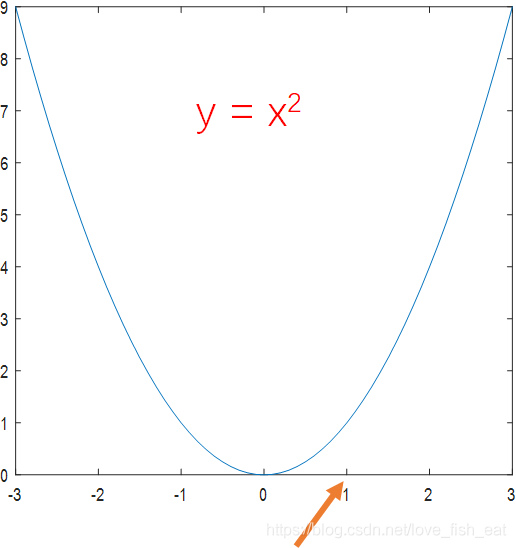
既然是從函數上的某一點出發,那麼不妨設想我們在x = 1 的地方,這個地方是不是極小值點呢,我們可以試探一下。
向右走0.5,發現f(1.5) > f(1),說明這個方向是上升的方向,不應該選擇這個方向;
向左走0.5,發現f(0.5) < f(1),說明這個方向是下降的方向,選擇這個方向;
再向左走0.5,發現f(0) < f(0.5),說明這個方向是下降的方向,選擇這個方向;
再向左走0.5,發現f(-0.5) > f(0),說明這個方向是上升的方向,不應該選擇這個方向。
至此,我們可以將x = 0作為極小值點。回顧這個過程,我們將尋找極小值點的過程抽象如下:
- 首先,選擇一個方向
- 試著沿該方向走一小步,並據此判斷該方向是否合理。如果合理,則走這一步;如果不合理,換一個方向
- 反覆重複第二步,直到找到極小值點
當然這裡還有幾點值得注意
- 第一,對於一元函數來說我們只有向左走或向右走兩個選項。換句話說,每一步我們的選擇是有限的,是可以列舉的。因此,這個方法我把它稱之為列舉試探法。
- 第二,判斷方向其實不必這樣試錯,直接求導就好。如果某點的導數值 > 0,說明在該點處函數是遞增的,為了找到極小值,應該向左走;而如果導數值 < 0,則反之向右走即可。
- 第三,這種方法是不一定能找到極小值的,能不能找到極值點受選擇的起始點以及每次前進的步長這兩個因素影響。
對於第二點,我們可以引出梯度的定義了。
梯度是一個向量,它總指向當前函數值增長最快的方向。而它的模長則是這個最快的增長率(導數)的值。想要得到梯度向量,也很簡單,它在x, y, z……等方向上的分量(座標)就是相應的導數值。於是我們求導就可以了。
對於一元函數,函數變化的方向只有兩個,我們定義一種一維的向量來表示梯度,比如5i,-5i。i前的數為正時,代表向量指向x軸正向;i前的數為負時,代表向量指向x軸負向。由下圖可以看出,按照上述定義規定的梯度向量自然的指向了函數增長的方向,是不是很神奇。
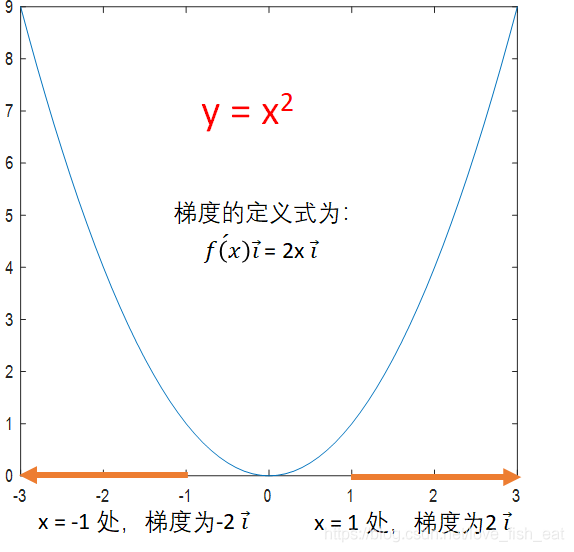
由於梯度的方向正是函數增長最快的方向,所以梯度的逆方向就成了函數下降最快的方向。當然對於一元函數來說,沒有最快的方向的概念,因為畢竟就兩個方向而已,根本沒得比。不過有了梯度,我們就可以進一步簡化上述尋找極小值點的過程:
- 首先,求出某點的梯度
- 沿梯度的反方向移動一小步
- 反覆進行第一、二步,直到找到極小值點
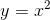 ,起始點x = 1為例,讓我們看看如何用梯度找到極值。
,起始點x = 1為例,讓我們看看如何用梯度找到極值。
初始x = 1, 步長step = 0.5
#在我們的例子裡,梯度的計算式為2xi。i是指向x軸正向的單位向量
求x = 1處的梯度為2i,梯度反方向為-i #注意這裡我們只關注梯度的方向,至於梯度的模長則不必在意
沿此方向走一步,x新 = x舊 + step * 負梯度方向上單位向量的座標 = 1 + 0.5 * (-1) = 0.5
求x = 0.5處的梯度為1i,梯度反方向為-i
沿此方向再走一步,x新 = 0.5 - 0.5 * 1 = 0
求x = 0處的梯度為0,說明到達極值點以上就是用梯度找極小值點的過程,也就是梯度下降演演算法所做的事情,其實不難理解對吧。
可以看出,相比於列舉試探法,梯度下降法明顯智慧了許多,它直接給出了正確的方向,不需要我們一步步試探了。此外,使用梯度下降法不必再關注具體的函數值,只需要把注意力放在導數上,而且只關注一階導數即可。
在後面,我們還將給上面提到的步長step換一個高大上的名字——學習率,這樣就完全是機器學習裡的叫法了。
這裡用到梯度的時候,我進行了單位化操作,其實也可以不進行這一步,這樣當函數變化比較劇烈的時候,移動的距離就比較多;函數變化比較平緩的時候,移動的距離就比較短。比如,在我們這個例子裡,只需一輪迭代就能得到結果了。
初始x = 1, 學習率step = 0.5
#在我們的例子裡,梯度的計算式為2xi。i是指向x軸正向的單位向量
求x = 1處的梯度為2i,梯度反方向為-2i #注意這裡我們既關注梯度的方向,也關注梯度的模長
沿此方向走一步,x新 = x舊 + step * 負梯度的座標 = 1 + 0.5 * (-2) = 0
求x = 0處的梯度為0,說明到達極值點好了說完了梯度,對於前面第三點提到的找不到極值的情形,我們舉兩個具體的例子
還是函數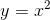 ,如果起始點選為0.4,而學習率仍為0.5,在採用單位化梯度向量的情形下,則無法找到事實上的極小值點
,如果起始點選為0.4,而學習率仍為0.5,在採用單位化梯度向量的情形下,則無法找到事實上的極小值點
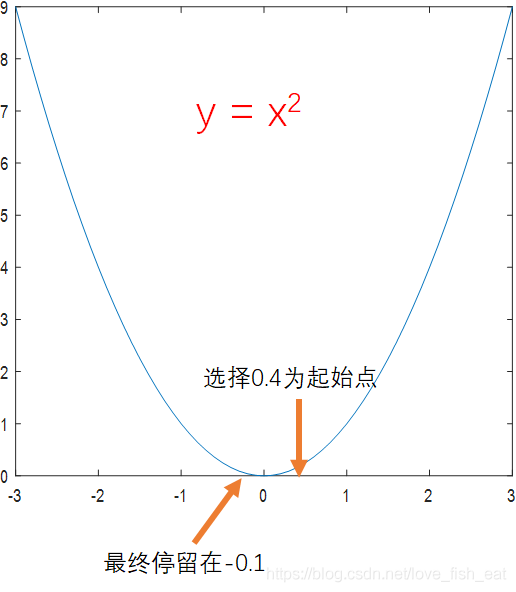
對於這種情況,我們可以通過減小學習率使結果儘可能精確,例如我們將學習率設定為0.1,就仍然能得到精確的結果。事實上,在實際操作中,一般也會把學習率設定為0.1。
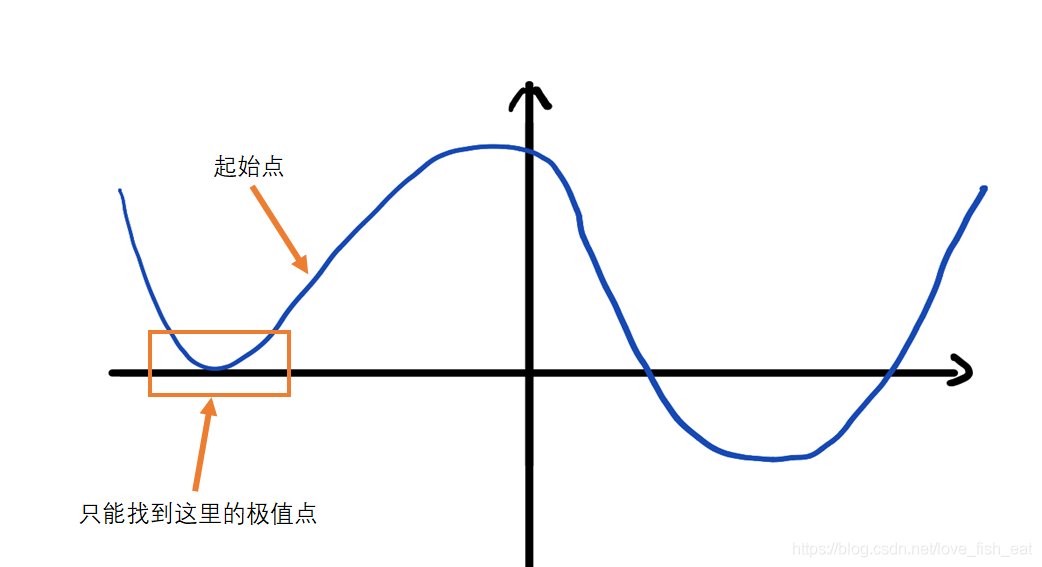
而對於這種有多個極值點的函數,這種方法是沒法找到全部極值點的,更遑論找到全域性的極值點了。這時,我們可以在演演算法裡加入一些隨機性,使其有一定概率跳出可能陷入的區域性極值點。
2.2 多元函數的梯度
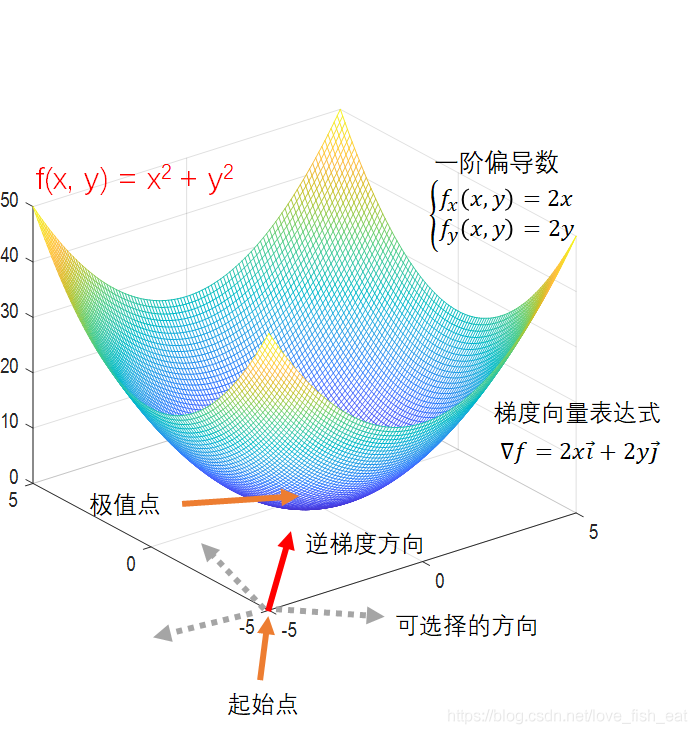
前面說過梯度下降演演算法的好處之一在於可以很方便的向多維推廣,現在我們以二元函數為例,看看梯度是如何幫助我們找到極值點的。
這次我們的函數變成了,起始點選擇為(-5, -5),學習率仍設定為0.5。現在我們的目標是從這個點出發,找到該函數的極值點,我們知道這個極值點應該是(0, 0)。
這裡與一元函數有幾點不同:
- 首先,二元函數描述的是一個自變數和兩個因變數之間的關係,也就是說函數的定義域是一個二維平面,我們要找的極值點就在這個二維平面上。
- 其次,由於是在二維平面上尋找極值點,我們每一步可以選擇的方向不再侷限於一維時的向左或向右,而是瞬間變成了無窮多個方向。因此,列舉試探法徹底宣告失效。還好我們有更智慧的梯度下降法。
- 一元梯度定義式裡的導數現在已經換成了多元函數的偏導數。
好了,現在演演算法開始:
起始點座標(-5,-5), 學習率step = 0.5
#在我們的例子裡,梯度的計算式為2xi + 2yj。i和j分別是指向x軸正向和y軸正向的單位向量
求點(-5,-5)處的梯度為-10i-10j,負梯度為10i+10j,寫成座標形式就是(10,10)
在點(-5,-5)處沿此梯度走一步
根據公式 向量座標 = 終點座標 - 起點座標,得終點座標 = 起點座標 + 向量座標
這裡,終點座標是(x新, y新),起點座標是(x舊, y舊) = (-5, -5)
向量座標是負梯度座標 = (10,10),再考慮學習率step,就可以得到
(x新, y新) = (-5,-5) + 0.5 * (10, 10) = (0, 0)
求(0, 0)處的梯度為零向量,說明到達極值點將上述過程抽象,我們就得到了梯度下降演演算法的全部邏輯:
我們要找函數的極小值點(使函數取值儘可能小的那一組自變數),
因為,梯度的方向是函數值增長速度最快的方向,
所以,沿著梯度的反方向函數值下降最快,
所以,只要沿著梯度的反方向一步步逼近就有可能找到那一組使函數取值儘可能小的自變數
如何沿著梯度的反方向一步步逼近呢?
我們隨機指定一個起點座標(一組自變數取值),然後沿著梯度的方向求出未知的終點座標
梯度是一個向量,本身也具有座標
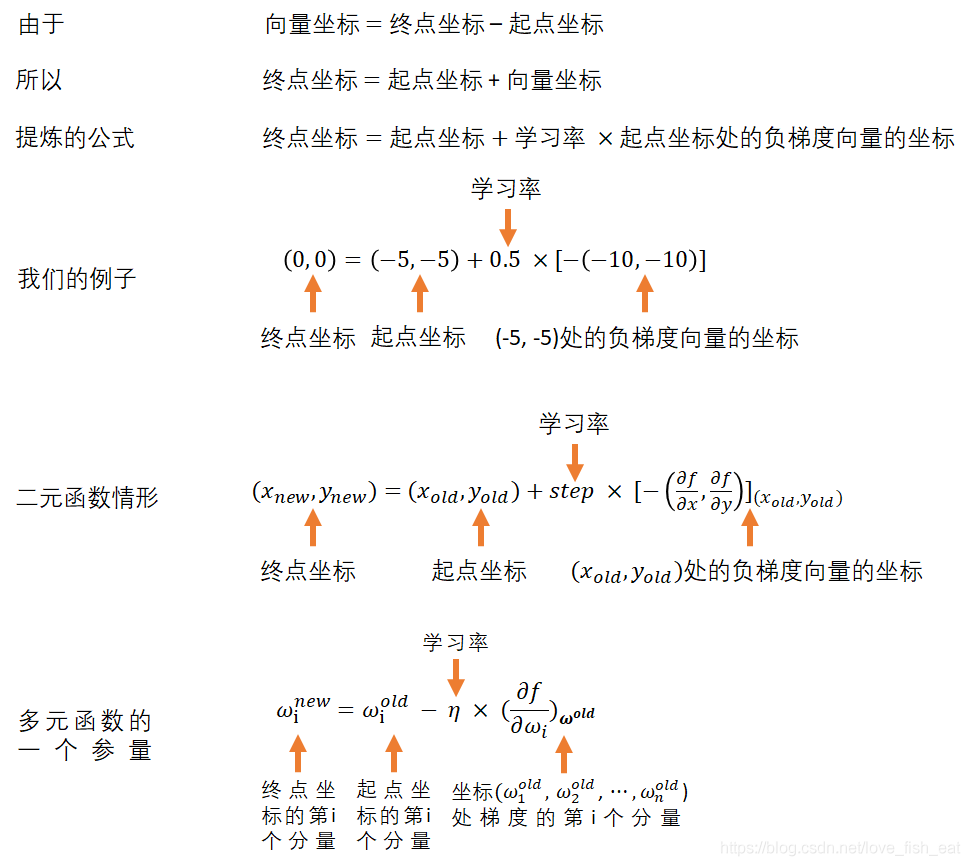
通過上面的迭代公式,無論是多少元的函數,它的一個個自變數們都會比較快的接近極值點(或者其近似)。這樣我們就可以找到一組自變數值,使得函數值儘可能的小。
2.3 小結
- 梯度的計算公式為
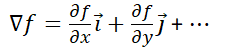
- 梯度是一個向量,它總指向當前函數值增長最快的方向,而它的模長則是這個最快的增長率(導數)的值。
- 梯度下降法是一種通過數值計算求解函數極值點的方法
- 其過程概括來說就是順著梯度的反方向一步步逼近可能的極值點
- 使用梯度下降法的理由在於求極值點的其他方法(如傳統法、列舉試探法)不具有可計算性,無法程式設計實現
- 梯度下降法可以很方便的向多元函數推廣,利於編寫程式
- 記住在這個過程中,我們要找的是極值點(使函數取極值的那一組自變數),而不是具體的極值
- 梯度下降法的劣勢在於不一定能找到全域性最優解
二、人工神經網路(ANN)
如果是第一次聽到人工神經網路這個名詞,不免會覺得比較高大上,好像我們已經可以模仿神祕的神經系統了。其實它只是一個數學模型而已。當然ANN的效果是令人眼前一亮的,好像計算機一下子真的有了人的能力,可以識人、識物。
但其實稍加抽象便能發現,這個東西無非就是個分類器,它的輸入是一張圖片,或者確切的說就是一堆代表畫素點的數值,而輸出則是一個類別。
所以說白了,所謂的人工神經網路其實就是一個超大規模的函數。
這就好比飛機和鳥兒的關係。讓飛機飛起來靠的不是依葫蘆畫瓢造一個人工鳥,而是靠流體力學中的原理建立數學模型,然後計算得出飛機的尺寸、造型,並設計相應的發動機。
1.神經元的數學模型
盜一張老師ppt裡的圖說明問題,可以看出ANN中的每一個節點(也就是所謂的神經元)就是這樣一個簡單的線性函數模型。
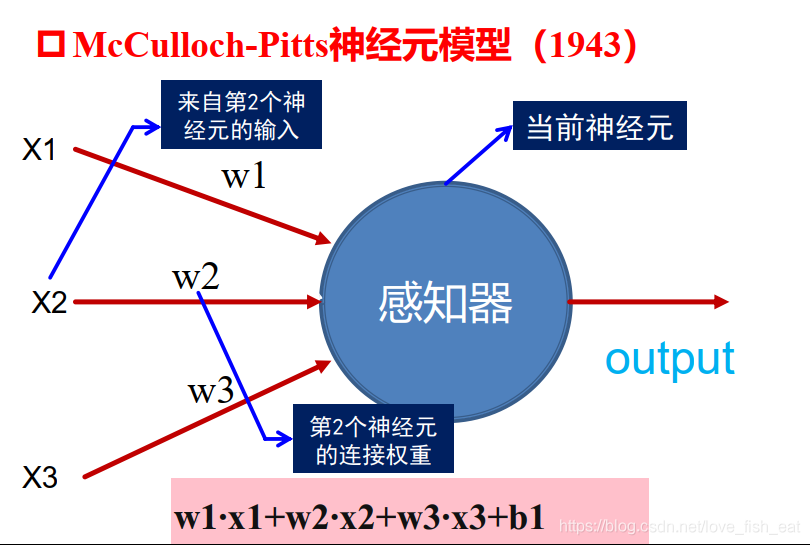
當然通過啟用函數我們可以製造一點非線性的因素,以提高模型的表達能力。這樣的話下面的神經元就代表這樣一個函數
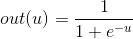 ,其中,
,其中,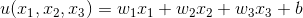 ,這裡w1, w2, w3, b都是引數,x1, x2, x3是函數的輸入,也就是因變數。
,這裡w1, w2, w3, b都是引數,x1, x2, x3是函數的輸入,也就是因變數。
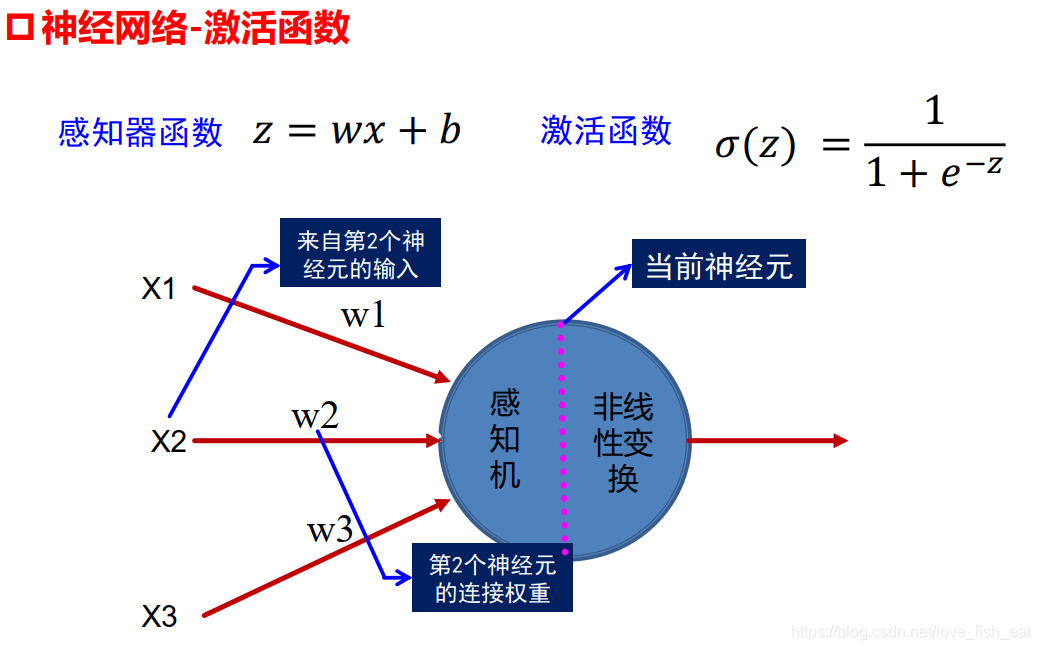
常用的啟用函數在這裡(仍然盜用老師的ppt,捂臉逃~)

以上就是所謂的人工神經元或者叫人造神經元,很多很多這樣的神經元按一定規則相連就構成了ANN,所以我才說ANN就是一個超大規模的函數而已。
是不是和你想象中的高大上的神經元大相徑庭,但是我們現在所謂的人工智慧其實就是這樣的數學模型而已。無論是簡單的影象分類器還是戰勝人類的AlphaGo,都是靠這樣的數學計算算出來結果的,而不是靠什麼化腐朽為神奇的力量。
2.ANN是如何煉成的?
知道了ANN的本質,現在就讓我們看看得到一個ANN需要怎麼做?這裡,請留意我們會遇到不同功能的函數,千萬不要搞混了。
既然ANN是一個超大規模的函數,那麼首先我們做的就是搭建起這個函數的架構,也就是設計人工神經網路的架構。
這時這個函數就有一堆引數待定了。
接下來我們準備一堆訓練資料訓練ANN,也就是把上面提到的待定引數都給他確定了。
模型完成,可以使用。顯然,最關鍵的是第三步——確定未知引數。
這裡首先解釋訓練資料,我們知道ANN是一個分類器也是一個函數,這個函數讀取一些輸入值,經過複雜的計算後得到輸出值,這些輸出值可以被解釋為類別。而訓練資料就是輸入值和最後的輸出值都已知的一組資料,換句話說就是已知一組函數的自變數和因變數的對應關係。
再說的明白點,我們的任務就是,已知函數的架構、函數的一組輸入值和輸出值,但不知道函數的一些引數,現在要推出這些未知引數。我把這裡我們要求出的這個函數稱之為目標函數。於是,一言以蔽之,我們的任務就是求出目標函數的未知引數。
為了完成這個任務,我們引出另一個重要的概念——損失函數。
2.1 損失函數
在這裡,我們玩一點小心機。注意了,這裡很關鍵!!!
既然我們已知目標函數的一組輸入和輸出,而未知其引數,那麼我們不妨將計就計將這些未知引數直接視為因變數,而將目標函數的輸入直接代入進去,這樣我們不就得到了一個自變數是目標函數的所有未知引數且函數整體完全已知的函數了嗎?
這時,如果能找到一組合適的未知引數,這個函數應該能輸出和已知輸入對應的輸出完全一致的值。
於是我們可以通過作差比較定義損失函數了
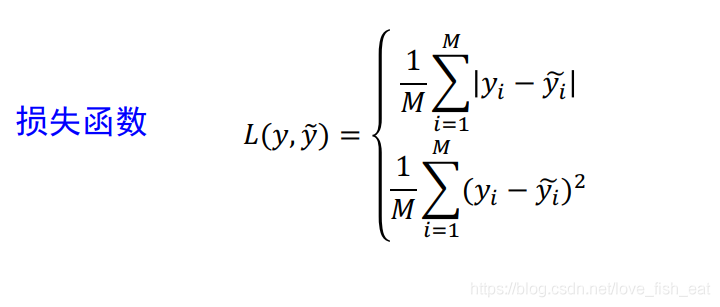
上圖給出了損失函數的兩種形式,為了計算方便,一般我們會選用第二種均方誤差的形式。這裡之所以出現了求和形式,是因為ANN的輸出端可能對應了多組函數,比如把一張圖片分成不同類別的概率。後面我們引入一個直觀的例子,一看便知。
這裡一定要注意,損失函數看起來雖然還有目標函數的影子,但實際已經完全不同了。我們列表比較一下
| 目標函數 | 損失函數 | |
|---|---|---|
| 表現形式 | 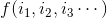 | 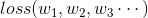 |
| 生成方式 | 事先搭好框架,再通過訓練得出待定引數 | 將目標函數的輸出與實際值作差得到框架,然後代入一個具體的訓練樣例(包括輸入值與標籤值) |
| 自變數 | 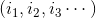 ——神經網路的輸入值(實際場合中可以是一張圖片的所有畫素值) ——神經網路的輸入值(實際場合中可以是一張圖片的所有畫素值) | 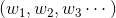 ——目標函數的待定引數 ——目標函數的待定引數 |
| 函數值(因變數)含義 | 屬於不同分類的概率 | 預測值與實際值的差值(越小越好) |
| 特點 | 我們最終想要得到的函數,可以用來作影象分類。是線性函數與非線性函數的組合,規模很大,自變數與引數都很多 | 用來求出目標函數的過渡函數。非負,最小值為0,一般要使用梯度下降法找到極值點 |
舉個例子看看函數變異的過程吧。設原函數為
,這是一個關於
的二元函數,其中a, b, c均是常數,也可以叫待定引數。現在我們給出一組具體的函數輸入值比如,令
把它們代入函數,並且將a, b, c視為變數,則函數變成了關於a, b, c的三元函數,記作
綜上,求目標函數的過程,就變成了尋找損失函數極值點的過程,而尋找極值點不正可以用上面介紹的梯度下降法實現嗎?
2.2 一個範例:關於鏈式求導和誤差反向傳播(BP)
行文至此,有關ANN的重要概念,我們還剩下鏈式求導和誤差反向傳播(BP)沒有提及,讓我們用一個範例融會貫通一下。
考慮下面這個簡單的ANN
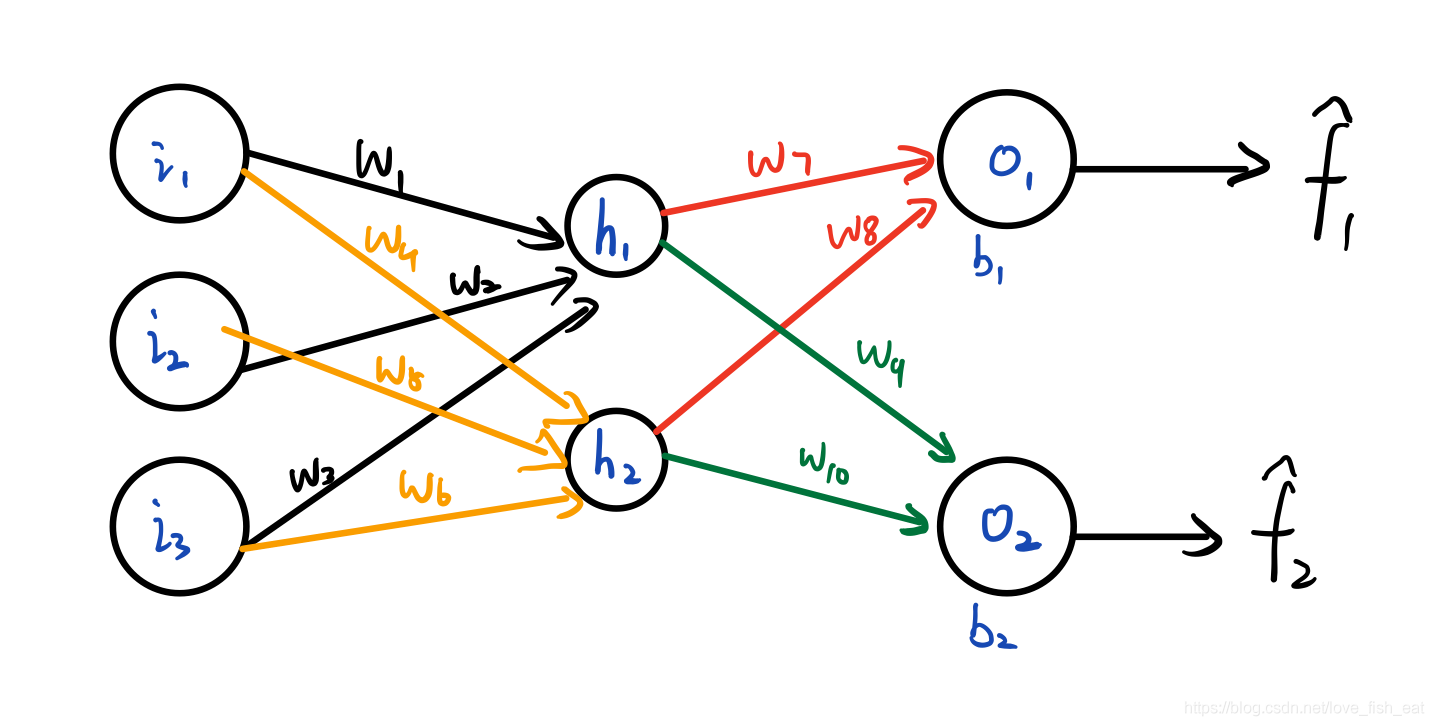
這個ANN只有4個神經元,分別是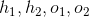 。它輸出兩個目標函數,均是輸入變數
。它輸出兩個目標函數,均是輸入變數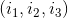 的函數,分別由神經元
的函數,分別由神經元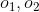 輸出。可以記為
輸出。可以記為
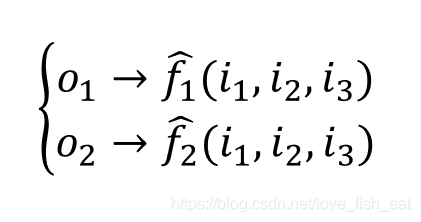
這裡給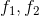 加上帽子,表示這兩個函數(即目標函數)的函數值是預測值,區別於訓練資料給出的實際標籤值。而
加上帽子,表示這兩個函數(即目標函數)的函數值是預測值,區別於訓練資料給出的實際標籤值。而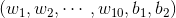 均是目標函數的待定引數,
均是目標函數的待定引數,
這裡我們假定神經元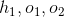 均採用sigmoid啟用函數,即
均採用sigmoid啟用函數,即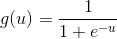 ,而神經元
,而神經元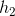 不採用啟用函數。
不採用啟用函數。
現在定義損失函數為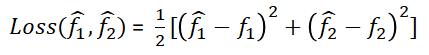
注意接下來我們會將具體的一組輸入變數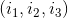 帶進去,這樣損失函數就被視作以
帶進去,這樣損失函數就被視作以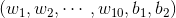 為自變數的多元函數(具體的自變數變化過程參見上文描述)。其中,
為自變數的多元函數(具體的自變數變化過程參見上文描述)。其中,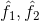 是中間變數,它們均是以
是中間變數,它們均是以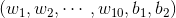 為自變數的多元函數。
為自變數的多元函數。
現在只要給出一個包含輸入輸出資料的訓練樣例,損失函數就成為不含未知引數的完全確定的函數。而我們要做的就是找到這個損失函數的極小值。
按照梯度下降演演算法的推導,此時我們只要按照下面的步驟就可以找出這個極小值:
隨機指定一組初始引數
---> [計算Loss函數關於各個引數的偏導數,注意這一步要代入引數的具體數值,也就是說這一步得到的是一個數 ---> 按照梯度下降的公式更新各個引數值直到滿足一定條件為止]
其中大括號 [] 裡的內容是需要反覆迭代的。
現在,我們以其中的幾個引數為例,看看在調整過程中會遇到什麼新問題。
先試試調整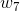 吧,這時我們需要求出損失函數對自變數
吧,這時我們需要求出損失函數對自變數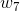 的偏導數值(注意是數值,不是表示式),為此寫出它的依賴關係:
的偏導數值(注意是數值,不是表示式),為此寫出它的依賴關係:
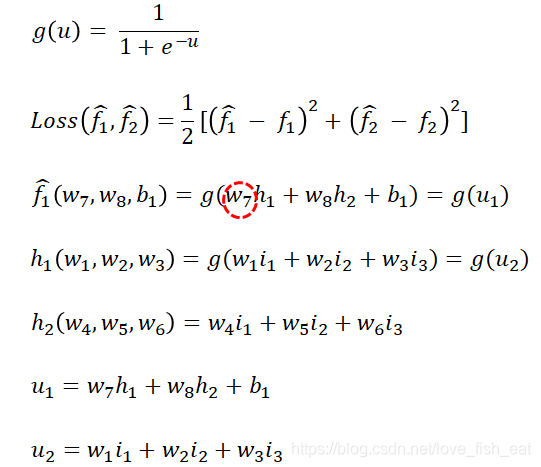
這裡,Loss函數依賴於變數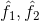 ,但
,但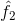 與
與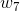 無關。回想多元函數求偏導數的規則,我們對
無關。回想多元函數求偏導數的規則,我們對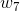 求導時,應將
求導時,應將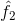 視為常數。
視為常數。
而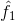 依賴於變數
依賴於變數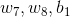 ,因此這裡應按照複合函數求導法則,即傳說中的鏈式求導法則,先讓Loss函數對變數
,因此這裡應按照複合函數求導法則,即傳說中的鏈式求導法則,先讓Loss函數對變數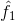 求導,再令
求導,再令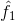 對
對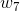 求導,即:
求導,即:
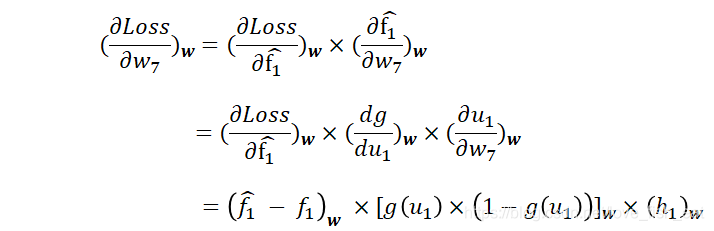
這裡有幾個要點:
- 首先,式子的每一項均加下標w,表示要將具體的一組
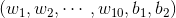 代入式子,得到一個數值
代入式子,得到一個數值 - 其次,當g(u)表示sigmoid函數時,對其求導的結果就是g(u) * [ 1 - g(u) ]
- 函數
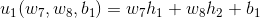 對變數
對變數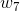 求偏導時,雖然
求偏導時,雖然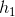 也是函數,但它是關於自變數
也是函數,但它是關於自變數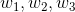 的函數,與
的函數,與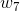 無關,因此視為常數。這樣,對
無關,因此視為常數。這樣,對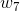 求偏導的結果就是
求偏導的結果就是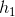
- 等式右端最後得出的三項,在給出一個訓練樣例,並指定初始引數
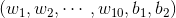 後,是可以獨立計算出結果的
後,是可以獨立計算出結果的
求出損失函數對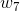 的偏導數值,我們就可以按照梯度下降演演算法推導的公式,調整這個引數了!
的偏導數值,我們就可以按照梯度下降演演算法推導的公式,調整這個引數了!
現在,再來看看靠前的引數是怎麼調整的,我們以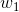 和
和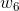 為例
為例
還是老規矩,對照神經網路圖,先寫出它的依賴關係:
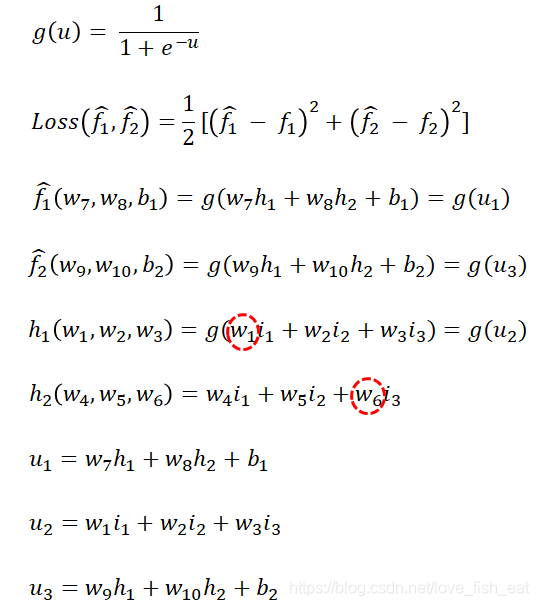
可以看出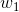 和
和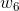 ,分別是函數函數
,分別是函數函數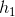 和
和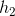 的變數,而函數
的變數,而函數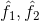 均與
均與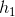 、
、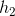 有關,所以Loss函數需要對
有關,所以Loss函數需要對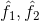 均求偏導。
均求偏導。
依然按照鏈式求導法則對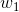 求偏導,有:
求偏導,有:
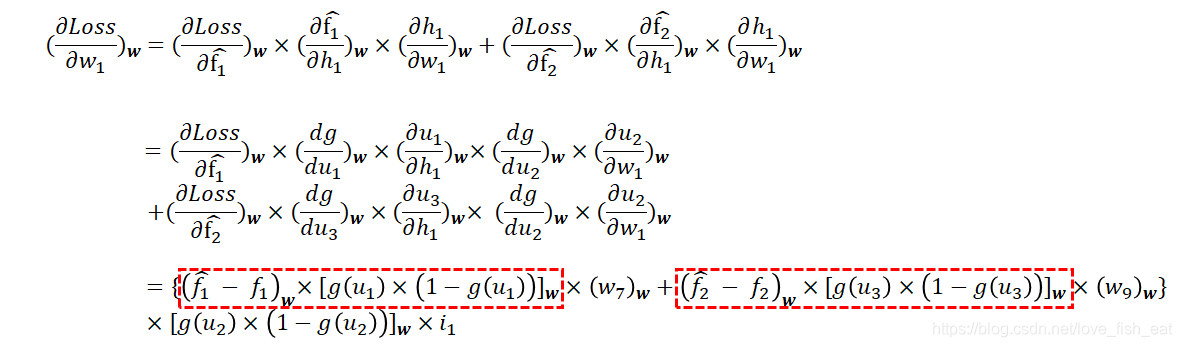
對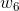 求偏導,有:
求偏導,有:
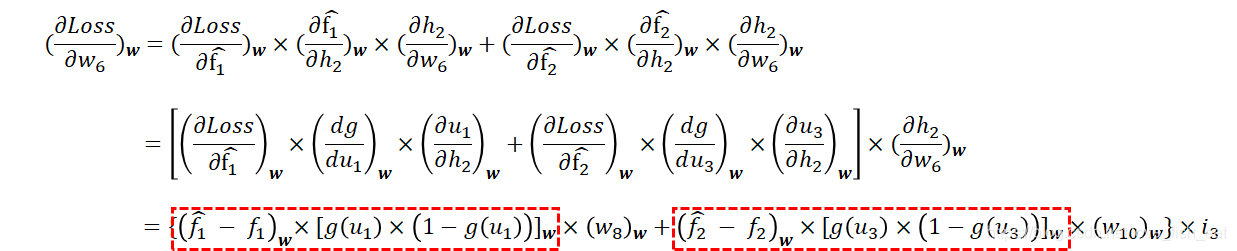
注意紅框圈出來的部分是不是有些眼熟?
事實上,這一部分已經在調整後層引數的時候計算過了(請回看計算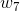 時的計算公式)。因此在程式設計時,可以讓程式儲存中間結果,這裡直接拿來用。
時的計算公式)。因此在程式設計時,可以讓程式儲存中間結果,這裡直接拿來用。
現在縱觀整個過程,我們驚奇的發現,對於ANN,
當我們需要使用它時,是從最前面給出輸入,然後一步步往後計算得出這個龐大複雜函數的輸出的;
而當我們需要訓練它時,則是從最後面的引數開始,一步步向前求導,調整各個引數的。並且計算前面的引數時一般都會用到之前計算過的中間結果。
這樣,ANN調整引數的過程就可以看作是一個誤差反向傳播(BP)的過程。
之所以會這樣反向傳播,是因為神經網路中靠後的引數依賴的中間變數少、複合層數少,而靠前的引數則經過層層複合,求導鏈會拉的很長。
2.3 最後的一點小問題
以上我們將求偏導的過程整個過了一遍,而求偏導只是梯度下降演演算法的一環。
程式跑起來之後,我們會對每一個訓練樣例,一遍遍的求偏導,直到基本上找到極小值點。
也就是說,按照梯度下降演演算法,每一個訓練樣例都會最終給出一組引數值。
一個訓練集中顯然會有多個訓練樣例,因此最終會得到好多組各不相同的引數值。
而ANN的訓練目標是確定一組引數值,得到一個有一定效果的很複雜的函數,
怎麼解決?
對每一個引數,我們可以將不同訓練樣例得出的不同值求一個平均。也可以構建一個更大的損失函數,即將每一個訓練樣例生成的損失函數求和,然後用梯度下降演演算法找到這個累計損失函數的極小值點。
這樣,我們就能通過訓練,最終確定ANN這個大函數的所有待定引數,然後用它來做一些神奇的事情。