規劃題解

規劃

原題連結:
https://www.luogu.com.cn/problem/P1642

題目

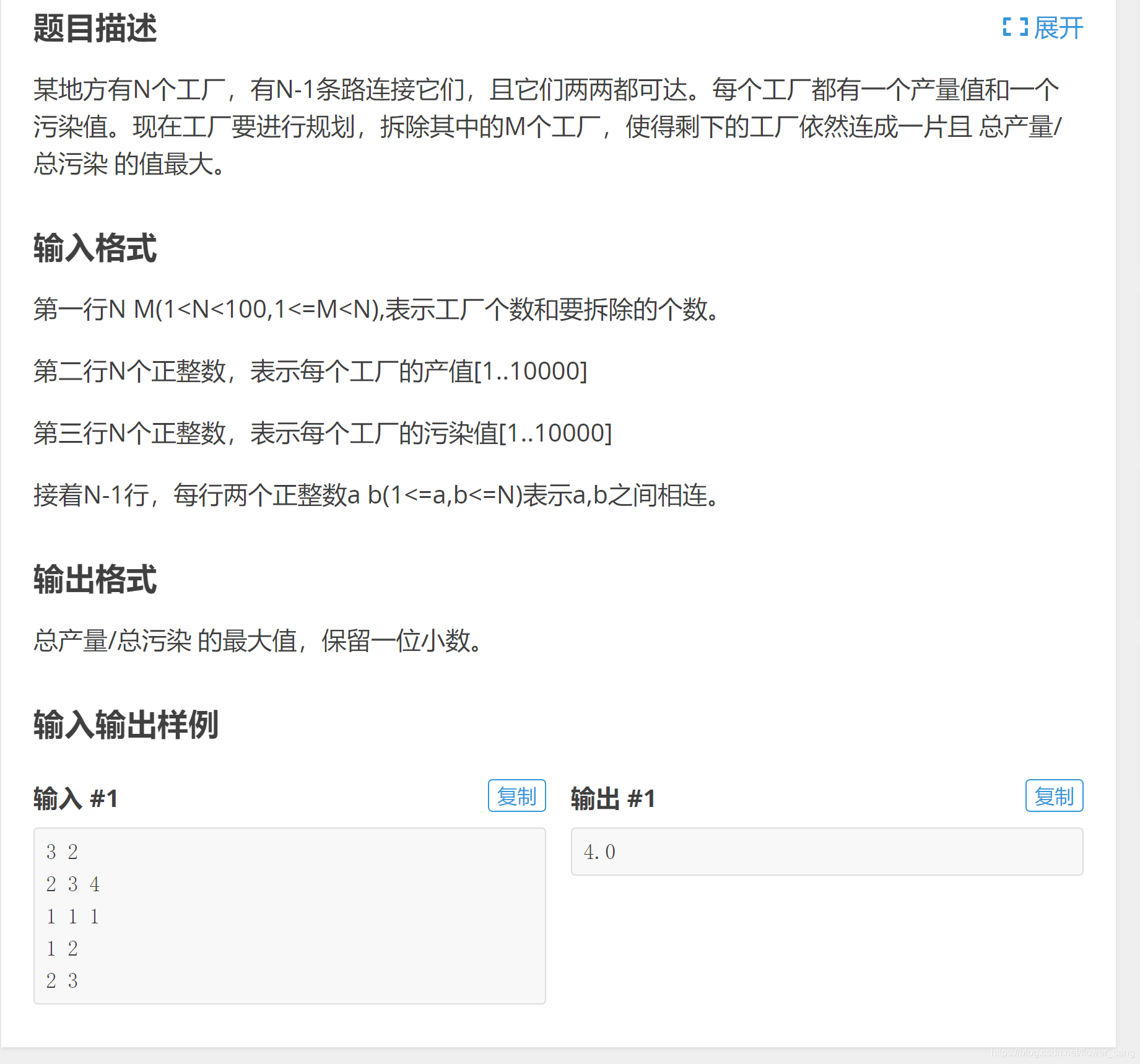
題解

首先看題， 求$\frac{\sum a_i}{\sum b_i}$的最大值不禁讓人聯想到0/1分數規劃， 然後再看， 這一張圖是一棵樹， 然後又要選擇剛好n - m個節點， 這不就是一個有依賴的揹包嗎？那麼就簡單了， 首先我們可以確定一個根節點， 然後我們進行遞迴， 每次搜到一個節點就按照分組揹包裝其子節點， 然後若是這樣選， 那此節點一定必須選， 就強制放入當前節點的揹包。

程式碼

#include <cstdio>
#include <algorithm>
using namespace std;

#define MAXN 100
#define INF 1<<30

double dp[MAXN + 5][MAXN + 5];//揹包
double sa[MAXN + 5], sb[MAXN + 5];//sa:汙染， sb：價值
double c[MAXN + 5];//sa - sb * mid
int q[MAXN + 5];//以i節點為根的子樹的節點個數
struct node {
	int ed;
	node *next;
}s[MAXN + 5];//鄰接表

void push (int x, int y) {
	node *p;
	
	p = new node;
	p->ed = y;
	p->next = s[x].next;
	s[x].next = p;
}

void dfs (int l, int f, int m) {
	q[l] = 1;
	dp[l][0] = 0;
	for (node *i = s[l].next; i != 0; i = i->next) {
		if (i->ed == f) {
			continue;
		}
		dfs (i->ed, l, m);
		q[l] += q[i->ed];
		for (int j = min(q[l], m); j >= 0; j --) {
			for (int k = 0; k <= j && k <= q[i->ed]; k ++) {
				dp[l][j] = max (dp[l][j], dp[l][j - k] + dp[i->ed][k]);
			}
		}
	}
	for (int i = min (m, q[l]); i >= 1; i --) {
		dp[l][i] = dp[l][i - 1] + c[l];
	}
}

int main () {
	int n, m;
	
	scanf ("%d %d", &n, &m);
	for (int i = 1; i <= n; i ++) {
		scanf ("%lf", &sa[i]);
	}
	for (int i = 1; i <= n; i ++) {
		scanf ("%lf", &sb[i]);
	}
	for (int i = 1; i < n; i ++) {
		int x, y;
		
		scanf ("%d %d", &x, &y);
		push (x, y);
		push (y, x);
	}
	
	double l = 0, r = 1000000;
	
	while (r - l > 1e-4) {
		for (int i = 1; i <= n; i ++) {
			for (int j = 0; j <= n - m; j ++) {
				dp[i][j] = -INF;
			}
		}
		
		double mid = (l + r) / 2;
		
		for (int i = 1; i <= n; i ++) {
			c[i] = sa[i] - sb[i] * mid;
		}
		dfs (1, 0, n - m);
		
		bool bl = 0;
		
		for (int i = 1; i <= n; i ++) {
			if (dp[i][n - m] > -0.000001) {
				bl = 1;
				
				break;
			}
		}
		if (bl) {
			l = mid;
		}
		else {
			r = mid;
		}
	}
	printf ("%.1lf", l);
}