【演演算法與資料結構 11】如何運用遞迴演演算法，看這一篇就夠了！

大家好！我是【AI 菌】，一枚愛彈吉他的程式設計師。我熱愛AI、熱愛分享、熱愛開源！這部落格是我對學習的一點總結與思考。如果您也對 深度學習、機器視覺、演演算法、Python、C++ 感興趣，可以關注我的動態，我們一起學習，一起進步~
我的部落格地址為：【AI 菌】的部落格
我的Github專案地址是：【AI 菌】的Github

文章目錄

我們都知道，不管是資料結構還是演演算法，它們的目標都是降低時間複雜度。資料結構是從資料組織形式的角度達成這個目標，而演演算法思維則是從資料處理的思路上去達成這個目標。

在前面的系列文章中，我們已經學習了各種資料結構的基礎知識：

【演演算法與資料結構 04】多圖講解——線性表、順序表、連結串列
 【演演算法與資料結構 05】後進先出的棧——順序棧、鏈棧知多少?
【演演算法與資料結構 06】先進先出的佇列 —— 順序佇列 || 迴圈佇列 || 鏈式佇列大盤點
 【演演算法與資料結構 07】陣列 —— 陣列的基本操作( 增刪查與時間複雜度的關係！)
【演演算法與資料結構 08】字串 —— 字串匹配演演算法（面試高頻考點！）
【演演算法與資料結構 09】什麼是樹、二元樹、二叉查詢樹？
【演演算法與資料結構 10】雜湊表——高效查詢的利器

從今天開始，我們將開啟演演算法思維的學習之路。下面，我們就來學習最常用的演演算法思維之一 —— 遞迴。

在這裡插入圖片描述

一、遞迴的原理

在數學與電腦科學中，遞迴（Recursion）是指在函數的定義中使用函數自身的方法。直觀上來看，就是某個函數自己呼叫自己。

遞迴有兩層含義：

遞迴問題必須可以分解為若干個規模較小、與原問題形式相同的子問題。並且這些子問題可以用完全相同的解題思路來解決；
遞迴問題的演化過程是一個對原問題從大到小進行拆解的過程，並且會有一個明確的終點。最後，從這個終點開始，把小問題的答案按照原路返回，原問題便得以解決。

簡而言之，遞迴的基本思想就是把規模大的問題轉化為規模小的相同的子問題來解決。在函數實現時，因為大問題和小問題是一樣的問題，因此大問題的解決方法和小問題的解決方法也是同一個方法。這就產生了函數呼叫它自身的情況，這也正是遞迴的定義所在。

總之，遞迴的實現包含了兩個部分：

遞迴主體。是解決若干相同子問題的主要思路。
終止條件。解決問題的函數必須有明確的結束條件，否則就會導致無限遞迴的情況

在這裡插入圖片描述

二、遞迴的演演算法思想

遞迴的數學模型其實就是數學歸納法，這個證明方法是我們高中時期解決數列問題最常用的方法。接下來，我們通過一道題目簡單回顧一下數學歸納法。

一個常見的題目是：證明當 n 等於任意一個自然數時某命題成立。

當採用數學歸納法時，證明分為以下兩個步驟：

證明當 n = 1 時命題成立；
假設 n = m 時命題成立，那麼嘗試推匯出在 n = m + 1 時命題也成立。

與數學歸納法類似，當採用遞迴演演算法解決問題時，我們也需要圍繞這兩個步驟去做：

當你面對一個大規模問題時，如何把它分解為幾個小規模的同樣的問題；
當你把問題通過多輪分解後，最終的結果，也就是終止條件如何定義。

以上就是遞迴的演演算法思想。我們總結一下，寫出遞迴程式碼的關鍵在於，寫出遞迴主體和找出終止條件。

對於遞迴主體，一般有兩種形式：遞推公式和遞推關係。

對於一些數學邏輯關係明顯，能用公式表達的問題，可採用遞推公式。
對於一些不易用公式表達的問題，要儘量發掘問題中的邏輯，用遞推關係表示。

三、建立遞推公式

對於一些數學邏輯關係明顯的問題，我們採用 遞推公式 + 終止條件 的方式來解決。下面以一道簡單的題目為例：

已知Fibonacci數列為：1、1、2、3、5、8…，求Fibonacci數列的第n個數是多少？

經過觀察，根據Fibonacci數列的規律，我們很容易知道：數列當前項的值等於前兩項之和。用數學公式表示為：

$F (n) = F (n - 1) + F (n - 2) ，其中 F (1) = F (2) = 1 。$

由此可知，當我們採用遞迴的方法來做時。遞推公式已經得到：F(n)=F(n-1)+F(n-2)；而終止條件就是：F(1)=F(2)=1。

遞推公式和終止條件都已經得出，下面就可以用程式碼錶示出來了：

#include <iostream>
using namespace std;

//Fibonacci數列函數 
int Fibonacci(int n)   
{
	if(n==1||n==2)
		return 1;
	else
		return Fibonacci(n-1)+Fibonacci(n-2);
}

int main()
{
	int n=0;
	cin>>n;
	//輸出Fibonacci數列第n個數 
	cout<<Fibonacci(n);  
	return 0;
}

以上就是 遞推公式 + 終止條件 的遞迴演演算法思想。我們總結一下，寫出遞迴程式碼的關鍵在於，寫出遞推公式和找出終止條件。

也就是說我們需要：首先找到將大問題分解成小問題的規律，並基於此寫出遞推公式；然後找出終止條件，就是當找到最簡單的問題時，如何寫出答案；最終將遞推公式和終止條件翻譯成實際程式碼。

四、建立遞推關係

對於一些不易用公式表達的問題，可以儘量發掘問題中的邏輯關係，用 遞推關係+終止條件 的方式解決。

4.1 簡單範例：反向列印字串

為了理解如何建立遞推關係，我們先從一個簡單的範例入手：

以相反的順序列印字串。

當然，你可以使用迭代的辦法輕而易舉地解決這個問題，即從字串的最後一個字元開始遍歷字串。但是如何遞迴地解決它呢？

遞迴演演算法思路：

首先，我們可以將所需的函數定義為 printReverse(str[0…n-1])，其中 str[0] 表示字串中的第一個字元。然後我們可以確定如下的遞推關係，分兩步完成給定的任務：

printReverse(str[1…n-1])：以相反的順序列印子字串 str[1…n-1] 。
print(str[0])：列印字串中的第一個字元。

請注意，我們在第一步中呼叫函數本身，根據定義，它使函數遞迴。下面給出程式碼：

#include<iostream>
#include<stdio.h>
using namespace std;

// 遞迴函數 
void printReverse(const char *str) 
{
  // 終止條件 
  if (!*str) 
    return;
  // 遞迴函數 
  printReverse(str + 1);
  // 列印首字元 
  putchar(*str);
}

int main()
{
	// 初始化字元陣列 
	char s1[] = "Hello World!";
	// 呼叫遞迴函數 
	printReverse(s1);
	return 0;
}

執行結果：
在這裡插入圖片描述
以上就是遞推關係+終止條件的遞迴演演算法思想。我們總結一下，對於一些不易用公式表達的問題，寫出遞迴程式碼的關鍵在於，寫出遞推關係和找出終止條件。

4.2 簡單範例：反轉字串

為了更深一步理解遞推演演算法，我們在上題的基礎上，增大了難度。問題如下：

編寫一個函數，其作用是將輸入的字串反轉過來。輸入字串以字元陣列 char[] 的形式給出。不要給另外的陣列分配額外的空間，你必須原地修改輸入陣列、使用 O(1) 的額外空間解決這一問題。你可以假設陣列中的所有字元都是 ASCII 碼錶中的可列印字元。

由於空間複雜度上的約束，因此要保證兩個連續的遞迴呼叫之間沒有額外的空間消耗。也就是說，我們應該把問題劃分為獨立的子問題。

因此，關於如何劃分問題的一個想法是將每個步驟中的輸入字串減少為兩個元件：

首字元和末尾字元。
沒有首字元和末尾字元的其餘子字串。

然後我們可以獨立地解決這兩個部分。根據上述思想，我們可以提出如下遞推演演算法：

從輸入字串中獲取首字元和尾隨字元，即 str[0] and str[n-1]；
就地交換首字元和末尾字元；
遞迴呼叫函數來反轉剩餘的字串，也就是 reverseString(str[1…n-2])。

給定輸入字串「hello」，下面演示如何分解並解決它：

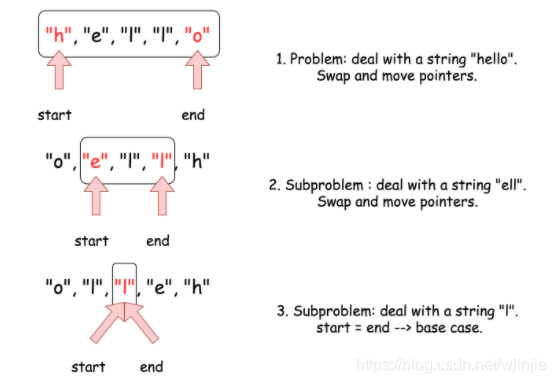
在這裡插入圖片描述
下面給出了上述演演算法的實現：

#include<iostream>
#include<string>
using namespace std;

// 遞迴函數 
void reverseString(int start, int end, string & s)
{
    if (start >= end) 
	{
    	return ;
    } 
    // 首尾交換 
    char tmp = s[start];
    s[start] = s[end];
    s[end] = tmp;
    // 遞迴函數 
    reverseString(start + 1, end - 1, s);
}

int main()
{
	string s1 = "Hello World!";
	reverseString(0, s1.size(), s1);
	cout<<"字串反轉後："<<s1<<endl;
	
	return 0;
}

執行結果：
在這裡插入圖片描述
可以看出，每次遞迴呼叫只需要常數級的記憶體，以便交換前導和末尾字元。結果顯而易見，它滿足了問題的約束。