模板題

給定一個n個點m條邊的無向圖，圖中可能存在重邊和自環，邊權可能為負數。

求最小生成樹的樹邊權重之和，如果最小生成樹不存在則輸出impossible。

給定一張邊帶權的無向圖G=(V, E)，其中V表示圖中點的集合，E表示圖中邊的集合，n=|V|，m=|E|。

由V中的全部n個頂點和E中n-1條邊構成的無向連通子圖被稱為G的一棵生成樹，其中邊的權值之和最小的生成樹被稱為無向圖G的最小生成樹。

輸入格式
第一行包含兩個整數n和m。

接下來m行，每行包含三個整數u，v，w，表示點u和點v之間存在一條權值為w的邊。

輸出格式
共一行，若存在最小生成樹，則輸出一個整數，表示最小生成樹的樹邊權重之和，如果最小生成樹不存在則輸出impossible。

資料範圍
$1 \leq n \leq 500$ ,
$1≤m≤10^5$ ,

圖中涉及邊的邊權的絕對值均不超過10000。

輸入樣例：

輸出樣例：

以模板題為例子解釋

根據給出的案例如圖所示：
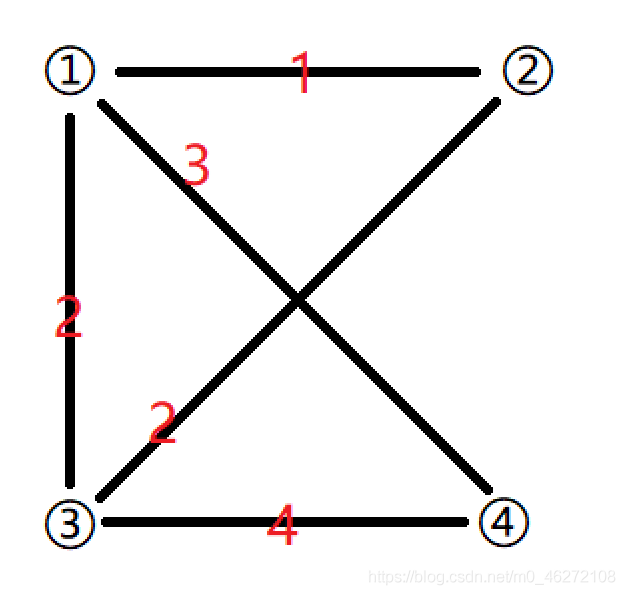
在這裡插入圖片描述
將所有的點距離初始化為正無窮。

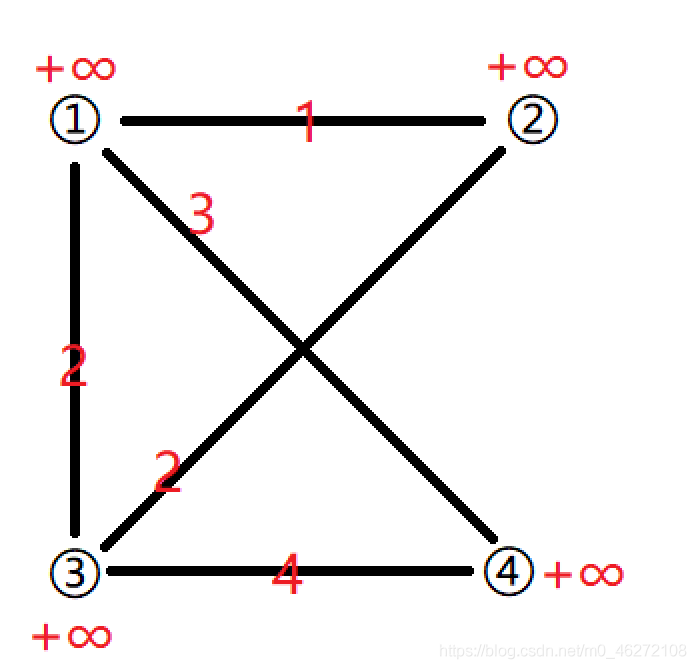
迭代n次 for (int i = 0; i < n; ++i ){ }
1.找到集合外最近的點，賦值為t
2.用t更新其他點到集合的距離（某一個點到集合的距離：這個點到集合內部的所有邊當中的長度最短的邊）
3.將t放到集合裡面去 st[t] = true;

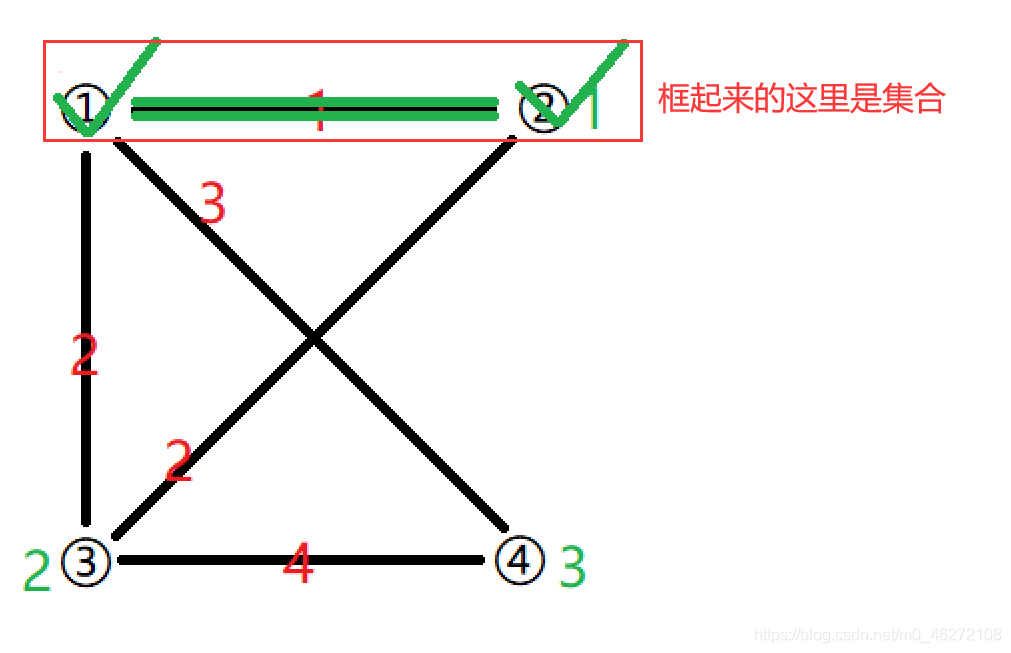
挑一個點放入集合中（這裡挑①）

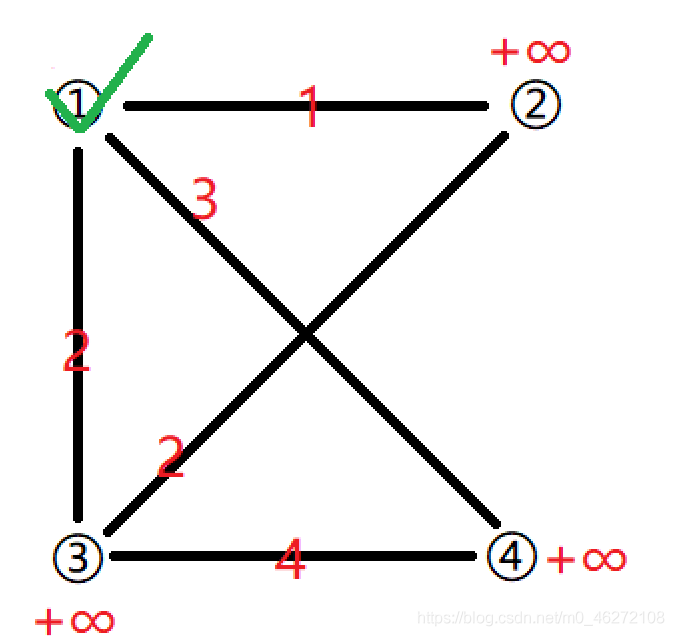
在這裡插入圖片描述
用這個點更新其它點到集合的距離。（看其它點有沒有一條邊能連向集合內部），則點②更新為1，點③更新為2，點④更新為3

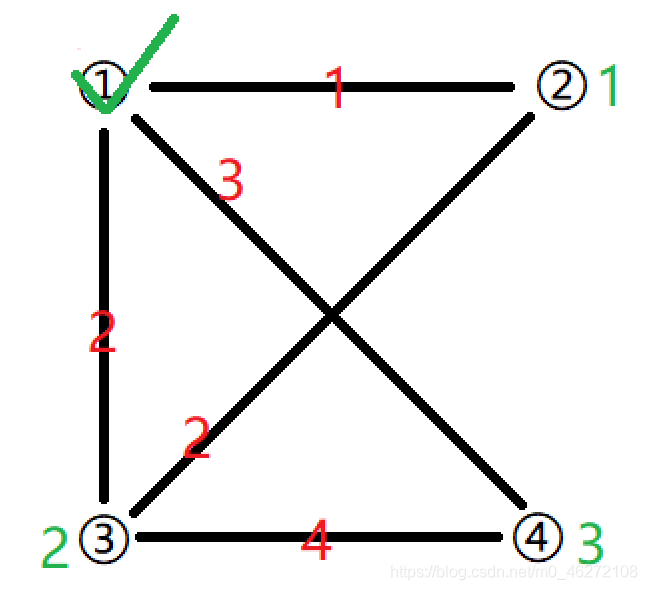
在其它點（②③④）中，選一個距離集合(這裡的集合只有點①)最近的點，即②，看是否能通過②這個點，更新其它點的距離，
①——②——③ 距離為3 大於 ①——③，所以不能更新，②沒有到④的線，所以總體無變化，則把點②加到集合中去，此時①——②這條邊是屬於集合的一條邊。

在這裡插入圖片描述
選下一個點③，①——④ 距離為3，①——③——④距離為6
總體無變化，將③加到集合中
由於①——③和②——③這兩條邊的距離相等，所以只選一條邊加入即可。
最後把④也加入集合。

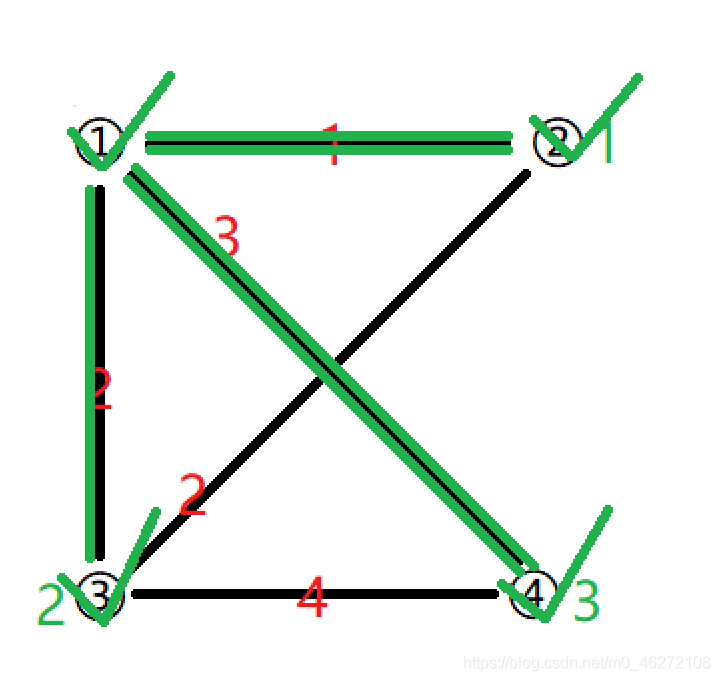
或者：

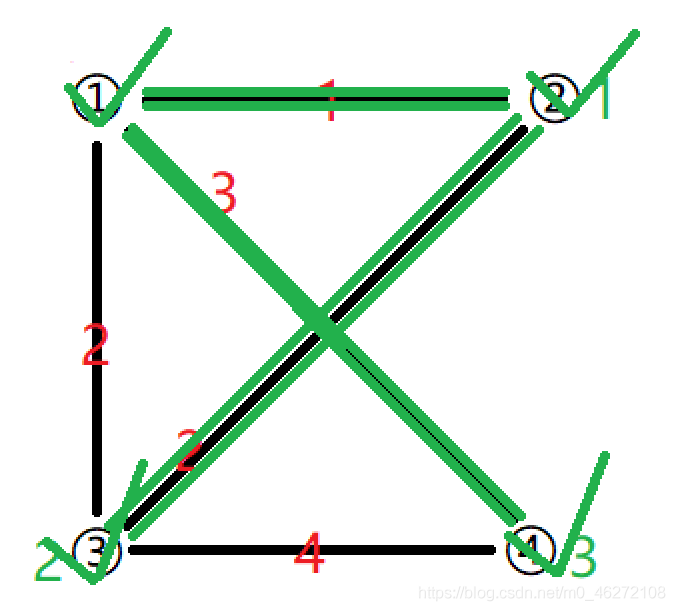
綠色的部分為集合。

生成樹： 每次選中的這個點，它的距離對應的那條邊就是生成樹裡的一條邊。
最終這個集合就是這個案例最終的最小生成樹。

最小生成樹案例：
地圖上有n個城市（已知座標），要在城市之間鋪設城際公路，使得城市與城市之間可以相互連通。問鋪設城際公路最小的總長度是多少？
（最小生成樹中正邊和負邊 ‘權重的正負’ 無關，都可以。）
（集合：代表當前已經在連通塊的所有點)

AC程式碼：（程式碼有詳細的註釋！）

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>

#define inf 0x3f3f3f3f
using namespace std;

const int N = 510;

int n, m;//n代表點，m代表邊
int g[N][N];//鄰接矩陣
int dist[N];//距離
bool st[N];//判斷該點是否在集合內

int prim() {
    memset(dist, inf, sizeof dist);//所有距離初始化為正無窮
    
    //n次迭代
    int res = 0;//存最小生成樹裡面所有長度之和
    for (int i = 0; i < n; ++i) {
        //找到集合外，距離最短的點
        int t = -1;//初始化t == -1 表示我們當前還沒有找到任何一個點。
        for (int j = 1; j <= n; ++j) {
            //在集合外，t == -1還沒有找到任何一個點 || t的距離大於j的距離
            if (!st[j] && (t == -1 || dist[t] > dist[j])) {
                t = j;//就把t 更新成 j
            }
        }
        //如果不是第一個點，當前距離最近的點到我的距離都是正無窮，說明當前這個圖是不連通的，說明不存在最小生成樹
        if (i && dist[t] == inf) {
            return inf;
        }
        
        //如果只要不是第一個點，就把dist[t]加到最小生成樹的長度和裡面去。只要不是第一個點，dist[t]表示當前這個點和現在已經連好的生成樹裡面的某一條邊的長度。而且dist[t]代表一條樹邊，所以加上就可以了
        if (i) {
            res += dist[t];
        }
        st[t] = true;//將點加到樹裡面去。
        /* 這裡要先更新再累加，不然會出現自環問題，最小生成樹是不存在環的。*/
        //用t更新一下，其他點到 集合 的距離
        for (int j = 1; j <= n; ++j) {
            dist[j] = min(dist[j], g[t][j]);
        }
    }
    //結束之後，t存的就是當前距離最小的點
    
    return res;
}
int main()
{
    scanf("%d%d", &n, &m);
    
    memset(g, inf, sizeof g);//初始化為 +∞
    
    //讀入所有邊
    while(m--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        //無向圖，就是建一條從a到b，再建一條從b到a的就可以了
        g[a][b] = g[b][a] = min(g[a][b], c);//可能有重邊，求一個min即可
        
    }
    
    int t = prim();
    
    //如果最終t == inf，則證明不存在這樣的最小生成樹
    if (t == inf) {
        printf("impossible\n");
    } else {
        printf("%d\n", t);
    }
    
    return 0;
}

圖論 —— 最小生成樹（樸素Prim原理及模板題）

最小生成樹

模板題

以模板題為例子解釋

AC程式碼：（程式碼有詳細的註釋！）