前言

資料結構，一門資料處理的藝術，精巧的結構在一個又一個演演算法下發揮著他們無與倫比的高效和精密之美，在為資訊科技打下堅實地基的同時，也令無數開發者和探索者為之著迷。

也因如此，它作為博主大二上學期最重要的必修課出現了。由於大家對於上學期C++系列博文的支援，我打算將這門課的筆記也寫作系列博文，既用於整理、消化，也用於同各位交流、展示資料結構的美。

此係列文章，將會分成兩條主線，一條「資料結構基礎」，一條「資料結構拓展」。「資料結構基礎」主要以記錄課上內容為主，「拓展」則是以課上內容為基礎的更加高深的資料結構或相關應用知識。

歡迎關注博主，一起交流、學習、進步，往期的文章將會放在文末。

---

前面總結了線性表的基本使用。這一節我們來總結一下兩種常用的也是非常重要且特殊的線性結構——棧和佇列。

說它重要，是因為這種結構在日常生產中的大大小小事務中無時無刻不在用到。

例如程式呼叫函數時產生的儲存就是棧結構，所以我們常說「棧空間」，先呼叫的函數最後結束，後來函數內的區域性變數的空間都會在該函數結束時得到釋放，且不會影響到前面的函數。而計算機底層指令執行就是一種佇列結構，後來的指令最後執行。

不僅如此，在各種演演算法中，兩個資料結構也是頻頻入鏡。以最基本的兩種搜尋演演算法為例，深度優先和廣度優先就是基於這兩種結構對狀態進行的列舉。

另外，面對事務並行的場景，一種不錯的解決方案是使用佇列管理事務，將其佇列化後依次處理。常見的輸入輸出流也是位元組資料的佇列。物件導向中一個類範例化和釋放時他本身及其繼承的父類別關係就是棧的關係。

所以，這兩種基礎資料結構的重要性是不言而喻的。俗話說「基礎不牢，地動山搖」，要建立堅實可靠演演算法基礎和業務邏輯能力，本節基礎內容和下一節的應用擴充套件內容將會是一個繞不開的重點，那麼就讓我們開始吧：

本節思維導圖：

---

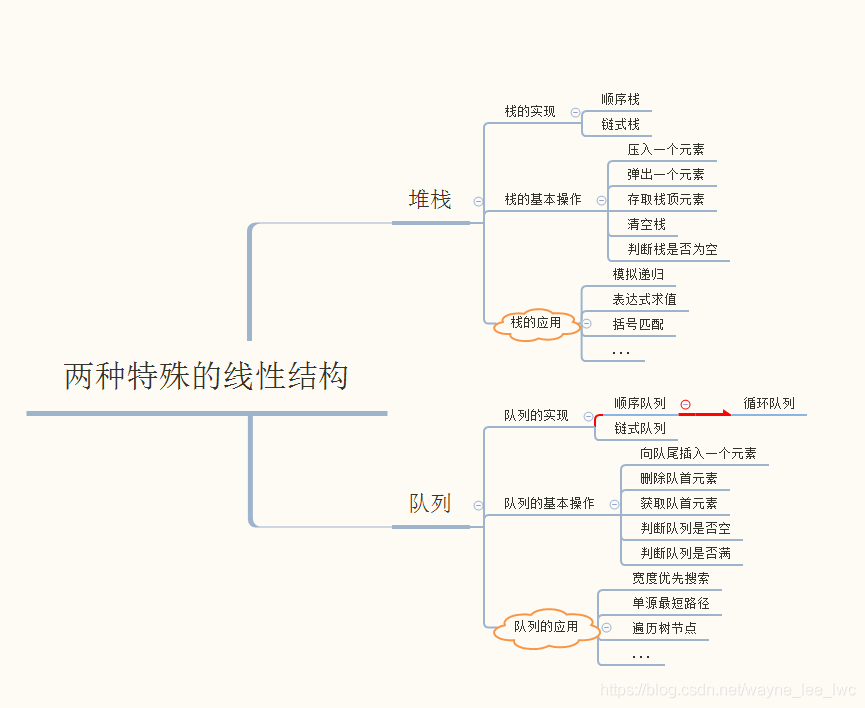
堆疊

堆疊簡稱棧，是一種首先得線性表，只允許表的同一段進行插入和刪除操作，且這些操作是按後勁消除的原則進行的。

進行插入和刪除的一段被稱為棧頂，另一端被稱為棧底。棧中沒有元素的時候被稱為空棧

順序棧

順序棧的儲存方式是順序的，使用陣列實現。

其特點就是棧的最大規模是確定的，因為陣列的大小無法動態改變。

順序棧的封裝

下面我們來封裝一個順序棧。最基本操作如下：

• 壓入一個元素（push）
• 彈出一個元素（pop）
• 獲得棧頂元素（peek）
• 清空棧（clear）
• 判斷是否為空（isEmpty）
• 判斷是否存滿（isFull）
• 獲得元素個數（size）

在順序棧中，我們只需要知道一個陣列的地址、當前元素個數以及陣列規模便可以完成棧的基本操作。

所以棧的類的原型以及建構函式可如下（以int元素為例）：

//C
typedef struct _Stack{
	int * elements;
	int maxLen;
	int size;
}Stack;

Stack * createStack(int maxLen){
	Stack * stack = (Stack *)malloc(sizeof(Stack));
	
	stack->maxLen = max(1,maxLen);
	stack->size = 0;
	stack->stack = (int *)malloc(sizeof(int) * min(1,maxLen));
	
	return stack;
}

//java
public class Stack {
	private int[] elements;

	private int maxLen;
	
	private int size;
	
	public Stack(int maxLen) {
		this.maxLen = Math.max(1,maxLen);
		
		elements= new int[maxLen];
		
		size = 0;
	}
}

判斷是否空/滿

有了這樣的原型，判斷一個棧是否空或者滿就很簡單了。

空就是當前規模為0，滿就是當前規模和最大規模相同。

//C
int isEmpty(Stack * stack){
	return stack->size == 0;
}

int isFull(Stack * stack){
	return stack->size == stack->maxLen;
}

public boolean isEmpty() {
	return size == 0;
}
public boolean isFull() {
	return size == maxLen;
}

獲得當前棧中元素數量

在確定了棧的原型之後，這個問題就變成了一個送分題，因為棧中元素數量就在裡面存著。

//C
int size(Stack * stack){
	return stack->size;
} 

public int size() {
return size;
}

壓入一個元素

在棧還有剩餘空間的條件下，插入一個元素只需要將該元素放置在陣列末尾 ，同時更新棧頂位置即可。

所以在執行插入操作之前，我們需要先對棧是否已滿進行判斷

//C
int push(int value,Stack * stack){
	if(isFull(stack)){
		return 0;	//	插入元素失敗，棧滿 
	}
	Stack->elements[stack->size] = value;
	stack->size++;
	return 1;
}

//java
public boolean push(int value) throws Exception {
	if(isFull()) {
		throw new Exception("棧滿不能新增元素");
	}
	elements[size] = value;
	size++;
	return true;
}

獲得棧頂元素

獲得棧頂元素，棧頂元素就是當前陣列中的最後元素，直接按照下標返回即可。

但在這之前需要判定一下棧是否為空。

//C
int peek(Stack * stack){
	if(isEmpty(stack)){
		return 0;
	}
	return stack->elements[stack->size - 1];
} 

public int peek() throws Exception {
	if(isEmpty()) {
		throw new Exception("空棧異常");
	}
	return elements[size - 1];
}

彈出棧頂元素

當棧頂元素存在時，順序棧只需要將棧頂指標向前移動一位即可表示刪除。對於空棧，可以選擇丟擲異常，也可以不做任何處理。

//C
int pop(Stack * stack){
	stack->size = max(0,stack->size - 1);
	return stack->size;
} 

public int pop() {
	size = Math.max(0, size - 1);
	return size;
}

清空棧

清空棧相當於刪除所有的元素，只需要將棧頂指標置零即可。

//C
int clear(Stack * stack){
	int size = stack->size;
	stack->size = 0;
	return size;
} 

//java
public int clear() {
	int size = this.size;
	this.size = 0;
	return size;
}

完整程式碼

//C
#include<malloc>

typedef struct _Stack{
	int * elements;
	int maxLen;
	int size;
}Stack;

Stack * createStack(int);
int isEmpty();
int isFull();
int push(Stack*,int);
int pop(Stack*);
int peek(Stack*);
int size(Stack*);
int clear(Stack*);


Stack * createStack(int maxLen){
	Stack * stack = (Stack *)malloc(sizeof(Stack));
	
	stack->maxLen = max(1,maxLen);
	stack->size = 0;
	stack->stack = (int *)malloc(sizeof(int) * min(1,maxLen));
	
	return stack;
}

int isEmpty(Stack * stack){
	return stack->size == 0;
}

int isFull(Stack * stack){
	return stack->size == stack->maxLen;
}

int push(int value,Stack * stack){
	if(isFull(stack)){
		return 0;	//	插入元素失敗，棧滿 
	}
	Stack->elements[stack->size++] = value;
	return 1;
}

int peek(Stack * stack){
	if(isEmpty(stack)){
		return 0;
	}
	return stack->elements[stack->size - 1];
} 

int pop(Stack * stack){
	stack->size = max(0,stack->size - 1);
	return stack->size;
} 

int size(Stack * stack){
	return stack->size;
} 

int clear(Stack * stack){
	int size = stack->size;
	stack->size = 0;
	return size;
} 

//java
public class Stack {
	private int[] elements;

	private int maxLen;
	
	private int size;
	
	public Stack(int maxLen) {
		this.maxLen = Math.max(1,maxLen);
		
		elements = new int[maxLen];
		
		size = 0;
	}
	public boolean isEmpty() {
		return size == 0;
	}
	public boolean isFull() {
		return size == maxLen;
	}
	
	public boolean push(int value) throws Exception {
		if(isFull()) {
			throw new Exception("棧滿不能新增元素");
		}
		elements[size] = value;
		size++;
		return true;
	}
	
	public int pop() {
		size = Math.max(0, size - 1);
		return size;
	}
	
	public int peek() throws Exception {
		if(isEmpty()) {
			throw new Exception("空棧無棧頂");
		}
		return elements[size - 1];
	}
	public int size() {
		return size;
	}
	
	public int clear() {
		int size = this.size;
		this.size = 0;
		return size;
	}
}

鏈式棧

鏈式棧是指使用鏈式儲存結構實現的棧。載體就是連結串列。

鏈式棧由於其使用連結串列實現，所以其相對於順序棧來說沒有了最大元素個數的上限。因此鏈式棧沒有了判斷棧滿的方法，因為鏈式棧理論上是無限的。

相較於順序棧來說，鏈式棧的一些操作會有些不同，最突出的是壓棧和彈棧。原因在於順序棧的棧頂指標並不是實際的元素指標，而是模擬的棧頂元素下標。再刪除元素的時候是直接將棧頂指標減一，棧頂元素自然就被排除在了棧之外，而並沒有被真正刪除。但是在鏈式棧這裡，刪除操作除了要將棧頂元素提出棧之外，還要切實的釋放掉它。

另外，鏈式棧的封裝和順序棧也不一樣，不再需要保留全部的陣列而是僅保留一個頭指標即可，這樣大大減少了封裝物件的大小。

最後一個問題，就是有關鏈式棧的棧頂在哪邊的問題，是放在鏈首好還是放在鏈尾好。其實這個問題非常好回答以至於基本上就是顯而易見的。由於棧結構的特殊性，我們需要頻繁的存取棧頂或插入刪除棧頂，而連結串列中唯一可以直接存取到的元素就是鏈首，要是存取鏈尾則需要每次遍歷整個棧，這個複雜度是我們不可接受的。

需要注意的是，鏈式棧中沒有哨位結點，而且基本操作也比單連結串列簡單
（當然者不代表使用哨位結點不行，只是實現起來會麻煩一些）

鏈式棧的封裝

在封裝具體的方法之前，先來封裝下鏈式棧物件和結構體。

//C
typedef struct _Node{
	int value;
	struct Node * next;
}Node;
typedef struct _LinkedStack{
	Node * head;
	int size;
}LinkedStack;

LinkedStack * createLinkedStack(){
	LinkedStack stack = (LinkedStack*)malloc(sizeof(LinkedStack));
	stack->head = NULL;
	stack->size = 0;
}

//java
public class LinkedStack {
	private class Node{
		int value;
		Node next;
	}
	
	private Node head;
	
	private int size;
	
	public LinkedStack() {
		size = 0;
		head = null;
	}
}

有了連結串列結構體和類宣告，下面就可以封裝對應的方法了。
當然，我們沒必要封裝所有的方法，只需要封裝幾個有明顯不同實現的方法即可。

壓棧

插入一個元素，需要新建一個結點並將它加入隊首。

//C
int push(LinkedStack * stack,int value){
	Node * node = (Node*)malloc(sizeof(Node));//新建一個結點
	/*設定結點資訊*/
	node->value = value;
	node->next = stack->head;
	/*插入結點*/
	stack->head = node;
	stack->size++;
	return 1;
}

//java
public boolean push(int val) {
	Node node = new Node();
	node.value = val;
	node.next = head;
	head = node;
	return true;
}

彈棧

彈出棧頂元素需要將棧頂元素踢出連結串列並釋放空間

//C
int pop(LinkedStack * stack){
	if(isEmpty()){
		return false;
	}
	Node * node = stack->head;//快取一下不然會出事
	stack->head = node->next;//踢出連結串列
	free(node);//釋放空間
	return 1;
}

public boolean pop() {
	if(isEmpty()) {
		return false;
	}
	/*注：java自帶垃圾回收機制，不需要手動釋放*/
	head = head.next;
	return true;
}

獲取棧頂元素

//C
int peek(LinkedStack * stack){
	if(isEmpty(stack)){
		return 0;
	}
	return stack->head->value;
}

public int peek() throws Exception {
	if(isEmpty()) {
		throw new Exception("空棧異常");
	}
	return head.value;
}

清空棧

清空棧的難點主要體現在將棧中的結點逐個釋放掉

//C
int clear(LinkedStack * stack){
	Node * node;
	while(stack->head){
		node = stack->head;
		stack->head = node->next;
		free(node);
	}
	size = 0;
	return 1;
}

//java
public boolean clear() {
	size = 0;
	head = null;
	//由於java存在垃圾回收機制，所以不用手動的釋放結點記憶體
	return true;
}

---

佇列

顧名思義，佇列在使用起來時就像現實生活中排隊的佇列一般。

佇列也是一種受限的線性結構，插入操作只能將元素放在一端而查詢和刪除操作只能對另一端使用。

這樣的限制導致了佇列元素特殊的先進先出特性。

這麼看，是不是挺像排隊的俯檢視的。

既然是特殊的線性結構，那就會有順序的和連結的兩種儲存模式，他們分別對應著順序佇列，和鏈式佇列，下面我們就來介紹並封裝他們。

順序佇列

順序佇列是指佇列元素在儲存空間上是順序的，它採用順序表也就是陣列儲存。

在陣列中表示佇列，需要隊首和隊尾兩個指標。

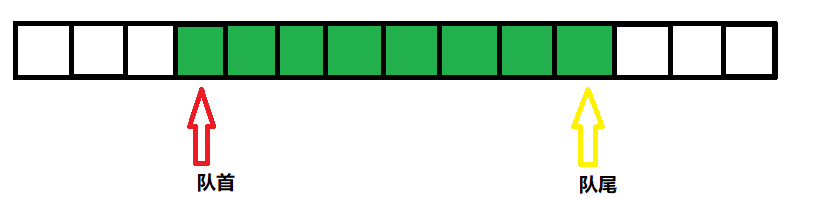
當需要插入一個元素時，僅需要將新的元素放置在隊尾，並將隊尾指標向後移動一格。
當需要彈出元素時，僅需要將隊首指標向後移動一格即可。

因為隊首和隊尾每次都是隻增不減，所以整個佇列看起來就像是在朝著隊尾方向前進。

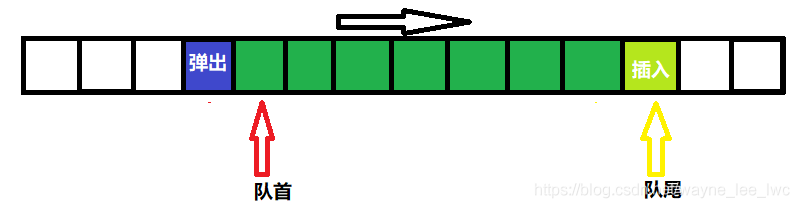
那麼空佇列也就是佇列中沒有元素時，其標誌就是隊首位於隊尾的右面一格。

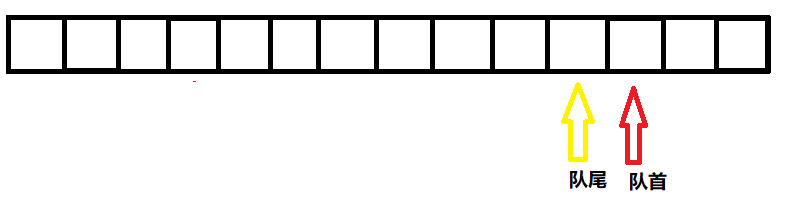
這樣一來，當加入一格新元素的時候，隊尾就會和隊首重合，這個唯一的元素就既是隊首也是隊尾。

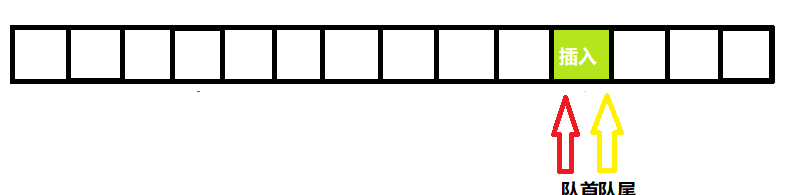
當刪除最後一個元素時，隊首會向前移動，位於隊尾的後方，回到空佇列的情況。

但是這樣有一個明顯的弊端，那就是佇列的插入次數是有限的。因為陣列的大小總是有上限的，每次插入都會使佇列向前移動一步，而每次彈出的空間卻不能在被佇列使用。這樣就造成了極大地不便，也是我們不能接受的。我們所希望的，是佇列的上限取決於佇列的長度，而非歷史插入次數。

迴圈佇列

於是我們便引出迴圈佇列來解決這個問題，迴圈佇列的思路就是將陣列首位相接，允許隊首和隊尾指標越過陣列的邊界再回到開始位置，這個操作可以使用取模運算來完成。

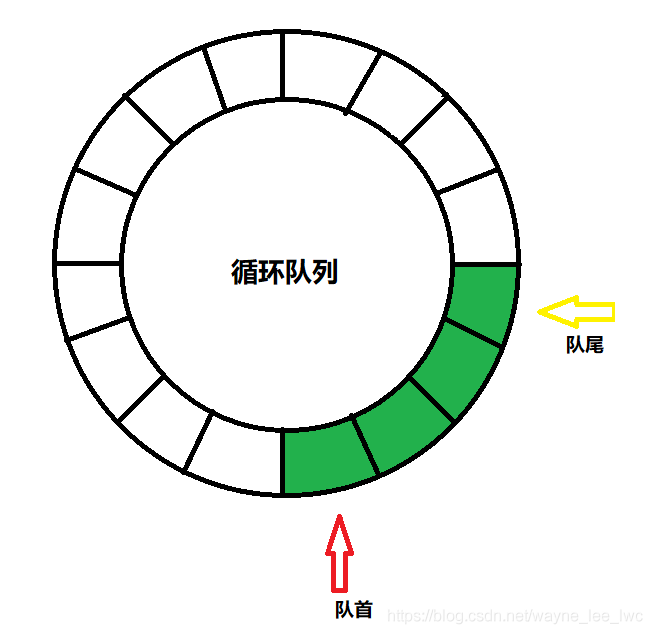
只是這樣的設計存在一個問題，那就是不能再像之前那樣根據隊首和隊尾的位置來判斷佇列是否為空了。隊尾指標出現在隊首指標後面時，還有可能是整個陣列都是佇列，且當佇列翻越陣列終點時，隊尾指標也會在隊首指標後面。


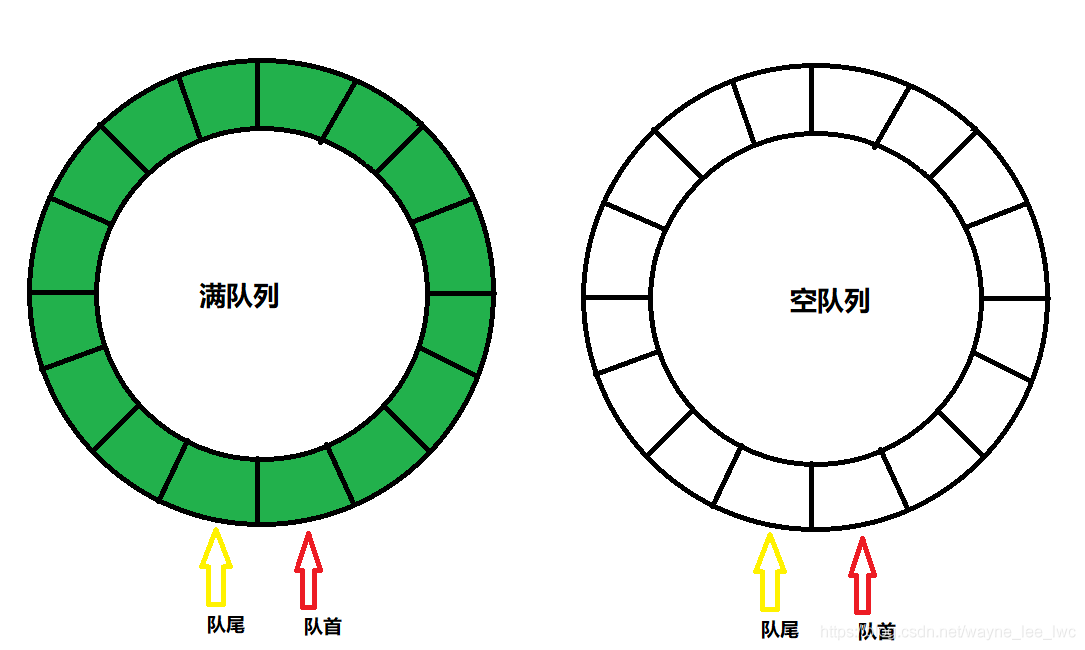
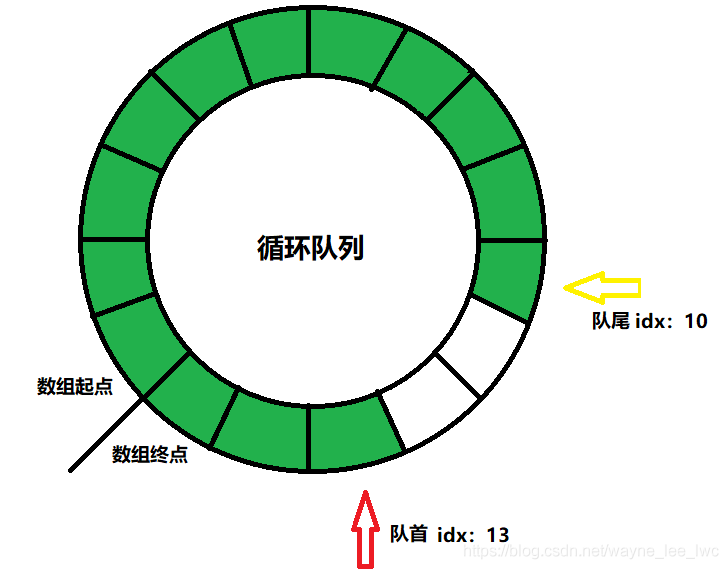
所以必須使用指標之外的辦法來管理陣列。

一個很直接的方法就是引入佇列中元素個數和陣列長度兩個屬性。這樣一來只需要在每次插入和刪除的時候維護一下元素個數即可，就可以根據元素個數及陣列長度來判斷佇列是否空或者滿。

順序佇列的封裝

封裝一個順序佇列，至少要完成一下的基礎操作：

• 入隊：向隊尾新增元素
• 出隊：刪除隊首元素
• 獲取隊首元素
• 判斷佇列是否為滿
• 判斷佇列是否為空

順序佇列的類

在封裝基礎操作之前，不妨先來給順序佇列的結構體和類封裝一下，這是所有操作的基礎。

經過上面的分析，實現順序佇列，就是用迴圈佇列實現，所以類成員至少需要包括以下三個資訊：

• 佇列陣列elements
• 陣列規模maxLen
• 佇列規模size
• 隊首位置head
• 隊尾位置tail

//C
typedef struct _ArrayQueue{
	int * elements;
	int maxLen;
	int size;
	int head;
	int tail;
}ArrayQueue;

ArrayQueue * createArrayQueue(int maxLen){
	ArrayQueue * queue = (ArrayQueue*)malloc(sizeof(ArrayQueue));
	maxLen = min(1,maxLen);
	queue->elements = (int*)malloc(sizeof(int) * maxLen);
	queue->maxLen = maxLen;
	queue->size = 0;
	queue->head = 0;
	queue->tail = maxLen - 1;
}

public class ArrayQueue {
	private int[] elements;
	private int maxLen;
	private int size;
	
	public ArrayQueue(int maxLen) {
		maxLen = Math.min(1, maxLen);
		elements = new int[maxLen];
		this.maxLen = maxLen;
		size = 0;
		head = 0;
		tail = maxLen - 1;
	}
}

獲取佇列規模

獲取佇列規模只需要返回其中儲存的size即可。

int size(ArrayQueue * queue){
	if(queue == NULL)
		return 0;
	return queue->size;
}

//java
public int size() {
return size;
}

判斷佇列是否為空

當佇列當前元素數量為0時佇列為空

//C
int isEmpty(ArrayQueue * queue){
	if(queue == NULL)
		return 0;
	return queue->size == 0;
}

//java
public boolean isEmpty() {
	return size == 0;
}

判斷佇列是否為滿

當佇列中元素個數與最大元素個數相等時，佇列為滿

//C
int isFull(ArrayQueue * queue){
	if(queue == NULL)
		return 0;
	return queue->size == queue->maxLen;
}

//java
public boolean isFull() {
	return size == maxLen;
}

入隊

入隊需要首先判斷佇列是否為滿，如果沒有滿則可以入隊，將新元素放到隊尾，同時維護隊尾指標和佇列規模。

//C
int push(ArrayQueue * queue,int element){
	if(isFull(queue))
		return 0;
	queue->tail = (queue->tail + 1) % queue->maxLen;
	queue->elements[tail] = element;
	queue->size++;
	return 1;
}

//java
public boolean push(int element) {
	if(isFull()){
		return false;
	}
	tail = (tail + 1) % maxLen;
	elements[tail] = element;
	size++;
	return true;
}

出隊

出隊之前需要先判斷佇列是否為空，若不為空則直接將頭指標向後移動一位同時維護佇列長度即可。

//C
int pop(ArrayQueue * queue){
	if(isEmpty(queue))
		return 0;
	queue->head = (queue->head + 1) % queue->maxLen;
	queue->size--;
	return 1;
}

//java
public boolean pop() {
	if(isEmpty())
		return false;
	head = (head + 1) % maxLen;
	size--;
	return true;
}

隊首元素

//C
int front(ArrayQueue * queue){
	if(isEmpty())
		return 0;
	return queue->elements[queue->head];
}

//java
public int front() throws Exception {
	if(isEmpty()) {
		throw new Exception("空佇列異常");
	}
	return elements[head];
}

清空佇列

清空佇列相當於將佇列恢復出廠設定，只需要將頭尾指標歸為並將元素個數置零即可。

//C
int clear(ArrayQueue * queue){
	queue->head = 0;
	queue->tail = -1;
	queue->size = 0;
	return 1;
}

//java
public boolean clear() {
	size = 0;
	head = 0;
	tail = -1;
	return true;
}

完整程式碼

//C
typedef struct _ArrayQueue{
	int * elements;
	int maxLen;
	int size;
	int head;
	int tail;
}ArrayQueue;

ArrayQueue * createArrayQueue(int maxLen){
	ArrayQueue * queue = (ArrayQueue*)malloc(sizeof(ArrayQueue));
	maxLen = min(1,maxLen);
	queue->elements = (int*)malloc(sizeof(int) * maxLen);
	queue->maxLen = maxLen;
	queue->size = 0;
	queue->head = 0;
	queue->tail = maxLen - 1;
}

int size(ArrayQueue * queue){
	if(queue == NULL)
		return 0;
	return queue->size;
}

int isEmpty(ArrayQueue * queue){
	if(queue == NULL)
		return 0;
	return queue->size == 0;
}

int isFull(ArrayQueue * queue){
	if(queue == NULL)
		return 0;
	return queue->size == queue->maxLen;
}

int push(ArrayQueue * queue,int element){
	if(isFull(queue))
		return 0;
	queue->tail = (queue->tail + 1) % queue->maxLen;
	queue->elements[tail] = element;
	queue->size++;
	return 1;
}

int pop(ArrayQueue * queue){
	if(isEmpty(queue))
		return 0;
	queue->head = (queue->head + 1) % queue->maxLen;
	queue->size--;
	return 1;
}

int front(ArrayQueue * queue){
	if(isEmpty())
		return 0;
	return queue->elements[queue->head];
}

int clear(ArrayQueue * queue){
	queue->head = 0;
	queue->tail = -1;
	queue->size = 0;
	return 1;
}

//java
public class ArrayQueue {
	private int[] elements;
	private int maxLen;
	private int size;
	private int head;
	private int tail;
	
	public ArrayQueue(int maxLen) {
		maxLen = Math.min(1, maxLen);
		elements = new int[maxLen];
		this.maxLen = maxLen;
		size = 0;
	}
	public int size() {
		return size;
	}
	
	public boolean isEmpty() {
		return size == 0;
	}
	
	public boolean isFull() {
		return size == maxLen;
	}
	
	public boolean push(int element) {
		if(isFull()){
			return false;
		}
		tail = (tail + 1) % maxLen;
		elements[tail] = element;
		size++;
		return true;
	}
	
	public boolean pop() {
		if(isEmpty())
			return false;
		head = (head + 1) % maxLen;
		size--;
		return true;
	}
	
	public int front() throws Exception {
		if(isEmpty()) {
			throw new Exception("空佇列異常");
		}
		return elements[head];
	}
	
	public boolean clear() {
		size = 0;
		head = 0;
		tail = -1;
		return true;
	}
}

注：這裡僅考慮完成基本的功能，對於更復雜的需求例如執行緒安全等並沒有考慮。

鏈式佇列

鏈式佇列和鏈式棧很類似，都是使用連結串列對佇列進行改造。

且仔細觀察不難發現，單連結串列的結構更適合實現佇列。

在鏈首，元素刪除更加容易。在鏈尾，元素無法直接得到其前驅，插入更加容易。

所以我們將鏈首當做隊首，將鏈尾當做隊尾。

與鏈式棧類似，鏈式佇列中也不需要哨位結點，且沒有最大長度限制

當佇列為空時首尾指標都為空。

鏈式佇列的封裝

首先還是先來封裝鏈式佇列的結構體和類，鏈式佇列僅需要記錄頭結點和尾結點的指標以及佇列規模，沒有佇列的最大長度限制。

//C
typedef struct _Node{
	int value;
	struct Node * next;
}Node;

typedef struct _LinkedQueue{
	Node * head;
	Node * tail;
	int size;
}LinkedQueue;

LinkedQueue * createLinkedQueue(){
	LinkedQueue * queue = (LinkedQueue*)malloc(sizeof(LinkedQueue));
	queue->size = 0;
	queue->head = NULL;
	queue->tail = NULL;
	return queue;
}

//java
public class LinkedQueue {
	private class Node{
		int value;
		Node next;
	}
	
	private Node head;
	private Node tail;
	private int size;
	
	public LinkedQueue() {
		size = 0;
		head = null;
		tail = null;
	}
}

同鏈式棧一樣，這裡僅封裝不太一樣的方法：

入隊

入隊時需要在隊尾新增元素，同時更新佇列大小。需要注意的是要單獨處理隊中沒有元素的情況。

//C
int push(LinkedQueue * queue,int value){
	Node * node = (Node*)malloc(sizeof(Node));
	node->value = value;
	node->next = NULL;
	if(isEmpty(queue)){//當隊中元素唯一時，該元素既是隊首又是隊尾
		queue->head = node;
		queue->tail = node;
	}else{
		queue->tail->next = node;
		queue->tail = node;
	}
	queue->size++;
	return 1;
}

//java
public boolean push(int value) {
	Node node = new Node();
	node.value = value;
	node.next = null;
	if(isEmpty()) {
		head = node;
		tail = node;
	}else {
		tail.next = node;
		tail = node;
	}
	size++;
	return true;
}

出隊

出隊的時候需要注意一下，當隊中最後一個元素要被踢出時，需要更新尾指標為空。

//C
int pop(LinkedQueue * queue){
	if(isEmpty(queue)){
		return 0;	
	}
	Node * node = queue->head;
	queue->head = node->next;
	if(queue->size = 1){
		queue->tail = NULL;
	}
	free(node);
	queue->size--;
	return 1;
}

//java
public boolean pop() {
	if(isEmpty()) {
		return false;
	}
	
	head = head.next;
	if(size == 1) {
		tail = null;
	}
	
	size--;
	return true;
}

清空佇列

同鏈式棧相似，清空佇列也需要將佇列中的元素結點釋放，同時維護佇列規模，並將頭尾指標還原為空。

//C
int clear(LinkedQueue * queue){
	queue->size = 0;
	Node * node;
	while(queue->head){
		node = queue->head;
		queue->head = node;
		free(node);
	}
	queue->tail = NULL;
	return 1;
}

//java
public boolean clear() {
	head = null;
	tail = null;
	size = 0;
	return true;
}

---

往期部落格

• 【資料結構基礎】資料結構基礎概念
• 【資料結構基礎】線性資料結構——線性表概念 及 陣列的封裝
• 【資料結構基礎】線性資料結構——三種連結串列的總結及封裝

---

參考資料：

• 《資料結構》（劉大有，楊博等編著）
• 《演演算法導論》（托馬斯·科爾曼等編著）
• 《圖解資料結構——使用Java》（胡昭民著）