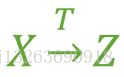函數依賴 主碼 主屬性 非主屬性 候選鍵 超鍵 詳解

最近做專案要搞資料庫看到正規化那一節頭腦發暈，概念都忘了，於是從網上搜羅並整理一下；
函數依賴部分參考：https://blog.csdn.net/jsj13263690918/article/details/79796275

主碼：主關鍵字（主鍵，primary key）是被挑選出來，作表的行的唯一標識的候選關鍵字（也稱為候選鍵）。一個表只有一個主關鍵字。主關鍵字又可以稱為主鍵。 主鍵可以由一個欄位（註釋1），也可以由多個欄位組成，分別稱為單欄位主鍵或多欄位主鍵。又稱主碼。並且它可以唯一確定表中的一行資料，或者可以唯一確定一個實體。

• 註釋1：欄位是邏輯設計中的資料描述，對應E-R圖中的屬性；也就是說主鍵可以由一個屬性組成也可以由多個屬性組成；

主屬性：在一個關係中，如果一個屬性是構成某一個候選關鍵字 (候選碼的屬性集中的一個屬性，則稱它為主屬性(Prime attribute)。

候選鍵：（自己的理解）比方說 成績表S（課程號，學號，成績）；此時課程號、學號就是候選鍵，能夠唯一確定成績，反之，其中任何一個主鍵，比如課程號或者是學號都不能確定成績；

非主屬性：表中的屬性除了主屬性就是非主屬性；

超鍵：超鍵包含候選鍵並且還有其他非主屬性；

函數依賴：

我們可以這麼理解（但並不是特別嚴格的定義）：若在一張表中，在屬性（或屬性組）X的值確定的情況下，必定能確定屬性Y的值，那麼就可以說Y函數依賴於X，寫作 X → Y。也就是說，在資料表中，不存在任意兩條記錄，它們在X屬性（或屬性組）上的值相同，而在Y屬性上的值不同。這也就是「函數依賴」名字的由來，類似於函數關係 y = f(x)，在x的值確定的情況下，y的值一定是確定的。

例如，對於表3中的資料，找不到任何一條記錄，它們的學號相同而對應的姓名不同。所以我們可以說姓名函數依賴於學號，寫作 學號 → 姓名。但是反過來，因為可能出現同名的學生，所以有可能不同的兩條學生記錄，它們在姓名上的值相同，但對應的學號不同，所以我們不能說學號函數依賴於姓名。表中其他的函數依賴關係還有如：

系名 → 系主任
學號 → 系主任
（學號，課名） → 分數
但以下函數依賴關係則不成立：

學號 → 課名
學號 → 分數
課名 → 系主任
（學號，課名） → 姓名
從「函數依賴」這個概念展開，還會有三個概念：

完全函數依賴

在一張表中，若 X → Y，且對於 X 的任何一個真子集（假如屬性組 X 包含超過一個屬性的話），X ’ → Y 不成立，那麼我們稱 Y 對於 X 完全函數依賴，記作 X F→ Y。（那個F應該寫在箭頭的正上方，沒辦法打出來……，正確的寫法如圖1）

圖1

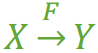
例如：

學號 F→ 姓名
（學號，課名） F→ 分數 （注：因為同一個的學號對應的分數不確定，同一個課名對應的分數也不確定）

部分函數依賴

假如 Y 函數依賴於 X，但同時 Y 並不完全函數依賴於 X，那麼我們就稱 Y 部分函數依賴於 X，記作 X P→ Y，如圖2。

圖2

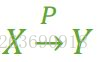
例如：

（學號，課名） P→ 姓名

傳遞函數依賴
假如 Z 函數依賴於 Y，且 Y 函數依賴於 X （感謝@百達指出的錯誤，這裡改為：『Y 不包含於 X，且 X 不函數依賴於 Y』這個前提），那麼我們就稱 Z 傳遞函數依賴於 X ，記作 X T→ Z，如圖3。

圖3