什麼是樹形DP？

概念：

給定一棵有N個節點的樹(通常是無根樹，也就是有N-1條無向邊)，我們可以任選一個節點為根節點，從而定義出每個節點的深度和每棵子樹的根。

在樹上設計動態規劃演演算法時，一般就以節點從深到淺(子樹從小到大)的順序作為DP的「階段」。DP的狀態表示中，第一維通常是節點編號(代表以該節點為根的子樹)。大多數時候，我們採用遞迴的方式實現樹形動態規劃。對於每個節點x，先遞迴在它的每個子節點上進行DP，在回溯時，從子節點向節點x進行狀態轉移。

如何樹形DP？

樹形DP一般可以解決三類問題：
①最大獨立子集
②樹的重心
③樹的直徑
而這三類問題是樹形dp題的基礎。

最大獨立子集

最大獨立子集的定義是，對於一個樹形結構，所有的孩子和他們的父親存在排斥，也就是如果選取了某個節點，那麼會導致不能選取這個節點的所有孩子節點。一般詢問是要求給出當前這顆樹的最大獨立子集的大小(被選擇的節點個數)。

最經典的莫過於這道題：

沒有上司的晚會

題目描述
Ural大學有N個職員，編號為1~N。他們有從屬關係，也就是說他們的關係就像一棵以校長為根的樹，父結點就是子結點的直接上司。每個職員有一個快樂指數。現在有個週年慶宴會，要求與會職員的快樂指數最大。但是，沒有職員願和直接上司一起參加宴會。

輸入格式
第一行一個整數N。(1≤N≤6000)
接下來N行，第i+1行表示i號職員的快樂指數Ri。(-128≤Ri≤127)
接下來N-1行，每行輸入一對整數L,K。表示K是L的直接上司。
最後一行輸入0,0。

輸出格式
第1行：輸出最大的快樂指數。

樣例
樣例輸入
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
樣例輸出
5

分析

建立一個二維DP，第一維是節點的編號(也是子樹的根)，第二維是這個根節點參加與否，比如dp[3][1]表示以3號節點為子樹的根，當它參會時整棵子樹的快樂指數和；dp[3][0]表示以3號節點為子樹的根，當它不參會時整棵子樹的快樂指數和；這樣就可以滿足最優子結構的性質了。
$d p [i] [0] = m a x (d p [k] [0], d p [k] [1])$

$d p [i] [1] = d p [k] [0] + w [i]$

注意：本題輸入的是一棵有根樹(制定了節點間的上下關係)，故我們需要先找出沒有上司的節點root作為根，DP的目標答案在 $m a x (d p [r o o t] [1], d p [r o o t] [0])$ 中。
時間複雜度為O(n)。

#include<cstdio> 
#include<algorithm>
#include<cstring>
#include<vector>
#define max(x,y) x>y?x:y
using namespace std;
const int M=1e5+5;
int a[M];
vector<int> G[M];
bool flag[M];
int dp[M][5];
void read(int &x) {
	x = 0; 
	int f = 1;
	char s = getchar(); 
	while (s > '9' || s < '0') { 
		if (s == '-') f = -1; 
		s = getchar(); 
	}
	while (s >= '0' && s <= '9') { 
		x = (x << 3) + (x << 1) + (s - '0');
		s = getchar(); 
	}
	x *= f;
}//讀優
void dfs(int x){
	dp[x][0]=0,dp[x][1]=a[x];
	for(int i=0;i<G[x].size();i++){
		int id=G[x][i];
		dfs(id);
		dp[x][0]+=max(dp[id][0],dp[id][1]);
		dp[x][1]+=dp[id][0];
	}
}
int main(){
	int n;
	read(n);
	for(int i=1;i<=n;i++){
		read(a[i]);
	}
	for(int i=1;i<n;i++){
		int l,k;
		read(l),read(k);
		G[k].push_back(l);
		flag[l]=true;
	}
	for(int i=1;i<=n;i++){
		if(flag[i]==false){
			dfs(i);
			printf("%d",max(dp[i][1],dp[i][0]));
			return 0;
		}
	}
	return 0;
}
/*
7 
1 1 1 1 1 1 1
1 3 
2 3 
6 4 
7 4 
4 5 
3 5 
0 0 
5
*/

樹的重心

樹的重心定義為，當把節點x去掉後，其最大子樹的節點個數最少(或者說成最大連通塊的節點數最少)，那麼節點x就是樹的重心。

在求樹的重心中，有以下幾個定理要用到：

1、刪除重心後所得的所有子樹，節點數不超過原樹的1/2，一棵樹最多有兩個重心，且相鄰；
2、樹中所有節點到重心的距離之和最小，如果有兩個重心，那麼它們距離之和相等；
3、兩個樹通過一條邊合併，新的重心在原樹兩個重心的路徑上；
4、樹刪除或新增一個葉子節點，重心最多隻移動一條邊。
~~反正現在看了也不懂~~

先來看一道題：

求樹的重心

題目描述
樹的重心定義為樹的某個節點，當去掉該節點後，樹的各個連通分量中，節點數最多的連通分量其節點數達到最小值。樹可能存在多個重心。如下圖,當去掉點1後，樹將分成兩個連通塊：（2,4,5），（3,6,7），則最大的連通塊包含節點個數為3。若去掉點2，則樹將分成3個部分，（4），（5），（1,3,6,7）最大的連通塊包含4個節點；第一種方法可以得到更小的最大聯通分量。可以發現，其他方案不可能得到比3更小的值了。所以，點1是樹的重心。

輸入格式
輸入：第一行一個整數n，表示樹的結點個數。（n<100）
接下來n-1行，每行兩個數i，j。表示i和j有邊相連。

輸出格式
輸出：第一行一個整數k，表示重心的個數。
接下來K行，每行一個整數，表示重心。按從小到大的順序給出。

樣例
樣例輸入
7
1 2
1 3
2 4
2 5
3 6
3 7
樣例輸出
1
1

分析

因為無根，所以要自己設一個根，這也是樹形dp常用的方法。

$d p [i] =$ $\sum_{j∈Son(i)}$ $d p [j] + 1$

那麼假設i是重心，在刪除 $i$ 之後 $m a x (d p [j]) (j \in S o n (i))$ 還要與i上面的所有節點(可看成一棵子樹)比，也就是 $n - d p [i]$ 。右圖中我們假設2號節點是重心，那麼除了他們兒子節點為根的子樹4和5以外，還有1367節點也可看成一棵子樹，所以 $f [i] = m a x (m a x (d p [j]), n - d p [i])$ (f[i]就是以i為重心的最大子樹節點數)，那麼答案就是 $m i n (f [i]) (i \in (1 n))$

搜尋時，還是遞迴到底層，回溯時進行累加，再利用重心的性質，所有
子樹的節點數不超過總節點數的1/2，更新flag的值，就可以找到重心節點了。

程式碼

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#define max(x,y) x>y?x:y
#define min(x,y) x>y?y:x
using namespace std;
const int M=1e5+5;
vector<int> G[M];
bool flag[M];
int dp[M],siz[M];
int ans=0x3f3f3f3f,cnt;
int n;
void dfs(int x,int y){
	int maxn=0;
	dp[x]=1;
	for(int i=0;i<G[x].size();i++){
		int id=G[x][i];
		if(id!=y){
			dfs(id,x);
			dp[x]+=dp[id];
			maxn=max(maxn,dp[id]);
		}
	}
	maxn=max(maxn,n-dp[x]);
	if(maxn<ans){
		ans=maxn;
		cnt=0;
		siz[++cnt]=x;
	}
	else if(maxn==ans){
		siz[++cnt]=x;
	}
}
void add_edge(int x,int y){
	G[x].push_back(y);
	G[y].push_back(x); 
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n-1;i++){
		int l,k;
		scanf("%d %d",&l,&k);
		add_edge(l,k);
	}
	dfs(1,0);
	printf("%d\n",cnt);
	sort(siz+1,siz+1+cnt);
	for(int i=1;i<=cnt;i++){
		printf("%d\n",siz[i]);
	}
	return 0;
}

樹的直徑

給定一棵樹,樹中每條邊都有一個權值,樹中兩點之間的距離定義為連線兩點的路徑邊權之和。樹中最遠的兩個節點(兩個節點肯定都是葉子節點)之間的距離被稱為樹的直徑,連線這兩點的路徑被稱為樹的最長鏈。後者通常也可稱為直徑。

有以下兩棵相同樹，但是根不同：(推薦一個作圖網站這裡)
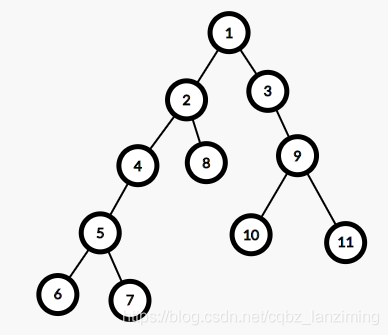
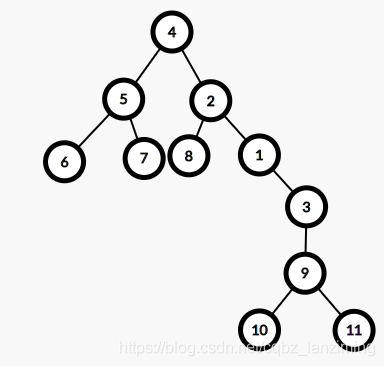
在這裡插入圖片描述

而兩棵樹的直徑卻是相同的，所以我們還是可以自定根節點

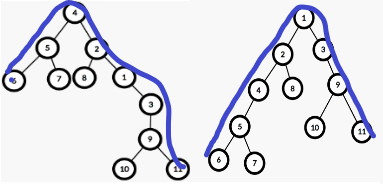
不妨設1號節點為根，「N個節點，N-1條邊的無向圖」就可以看作「有根樹」。設d[x]表示從節點x出發走向以x為根的子樹，能夠到達最遠節點的距離。設x的子節點為y1，y2，……，yt，edge(x, y)表示邊權，顯然有：
$d [x] = m a x$ { $d [y i] + e d g e (x, y i)$ } $(1 \leq i \leq t)$
接下來，我們可以考慮對每個節點x求出「經過節點x的最長鏈的長度」ans[x],整棵樹的直徑就是：
$m a x$ { $a n s [x]$ } $(1 \leq x \leq n)$

那麼，如何求ans[x]呢？我們用鏈式前向星存圖，依次遍歷以x為起點的所有連邊，用已經更新過的d[x]與沒有列舉到的x的連邊之和來更新ans[x]:
$a n s [x] = m a x (a n s [x], d [x] + d [y i] + e d g e (x, y i))$
然後再不斷更新
$d [x] = m a x (d [x], d [y i] + e d g e (x, y i))$

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#define max(x,y) x>y?x:y
#define min(x,y) x>y?y:x
using namespace std;
const int M=1e5+5;
struct node{
	int val,t;
	node(){}
	node(int T,int V){
		t=T,val=V;
	}
};
vector<node> G[M];
int ans,dp[M];
bool flag[M];
void dfs(int x){
	flag[x]=true;
	for(int i=0;i<G[x].size();i++){
		int yi=G[x][i].t;
		if(flag[yi]) continue;
		dfs(yi);
		ans=max(ans,dp[x]+dp[yi]+G[x][i].val);
		dp[x]=max(dp[x],dp[yi]+G[x][i].val);
	}
}
void add_edge(int x,int y,int z){
	G[x].push_back(node(y,z));
	G[y].push_back(node(x,z));
}
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n-1;i++){
		int u,v,w=1;
		scanf("%d %d",&u,&v);
		add_edge(u,v,w);
	}
	dfs(1);
	printf("%d",ans);
	return 0;
}

~~程式碼純手打，點個贊再走唄！~~

「總結」樹形DP