首先我們先要了解什麼是樹的重心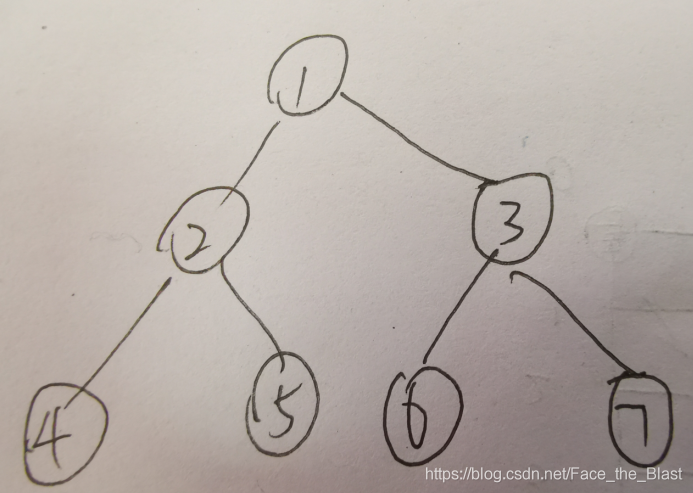

樹的重心定義為樹的某個節點，當去掉該節點後，樹的各個連通分量中，節點數最多的連通分量其節點數達到最小值。樹可能存在多個重心。如下圖,當去掉點1後，樹將分成兩個連通塊：$(2,4,5)$，$(3,6,7)$，則最大的連通塊包含節點個數為3。若去掉點2，則樹將分成3個部分，$(4)$，$(5)$，$(1,3,6,7)$最大的連通塊包含4個節點；第一種方法可以得到更小的最大聯通分量。可以發現，其他方案不可能得到比3更小的值了。所以，點1是樹的重心。

樹的重心的一些性質：

1. 刪除重心後所得的所有子樹，節點數不超過原樹的1/2，一棵樹最多有兩個重心，且相鄰；
2. 樹中所有節點到重心的距離之和最小，如果有兩個重心，那麼它們距離之和相等；
3. 兩個樹通過一條邊合併，新的重心在原樹兩個重心的路徑上；
4. 樹刪除或新增一個葉子節點，重心最多隻移動一條邊。

分析

任選一個節點為根，把無根樹變成有根樹，然後dp[i]表示以i為根的子樹的節點個數。不難發現：

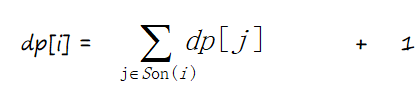
那麼假設i是重心，在刪除i之後$max(dp[j])(j\in Son(i))$還要與i上面的所有節點(可看成一棵子樹)比，也就是n-dp[i]。右圖中我們假設2號節點是重心，那麼除了他們兒子節點為根的子樹4和5以外，還有1367節點也可看成一棵子樹，所以$f[i]=max(max(dp[j]),n-dp[i])$

(f[i]就是以i為重心的最大子樹節點數)，那麼答案就是$min(f[i])(i\in (1n))$

搜尋時，還是遞迴到底層，回溯時進行累加，再利用重心的性質，所有子樹的節點數不超過總節點數的$1/2$，更新flag的值，就可以找到重心節點了。

程式碼

先以1為根節點，構造一棵樹

#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 1e5 + 5;
vector<int> a[MAXN], v[MAXN];
int de[MAXN], fa[MAXN], dp[MAXN], f[MAXN];
bool vis[MAXN], flag[MAXN];
int n, m, ans;
void Find_Son(int);
void Find_Father(int);
void dfs(int, int);
void Init();
void Read();
void DP(int);
int main() {
	Read();
	Init();
	DP(1);
	for(int i = 1; i <= n; i++)
		if(flag[i])
			ans++;
	printf("%d\n", ans);
	for(int i = 1; i <= n; i++)
		if(flag[i])
			printf("%d\n", i);
	return 0;
}
void Find_Son(int now) {
	for(int i = 0; i < a[now].size(); i++) {
		if(!vis[a[now][i]]) {
			v[now].push_back(a[now][i]);
			vis[a[now][i]] = 1;
			Find_Son(a[now][i]);
		}
	}
}
void Find_Father(int now) {
	for(int i = 0; i < v[now].size(); i++) {
		fa[v[now][i]] = now;
		Find_Father(v[now][i]);
	}
}
void dfs(int now, int step) {
	de[now] = step;
	for(int i = 0; i < v[now].size(); i++)
		dfs(v[now][i], step + 1);
}
void Init() {
	vis[1] = 1;
	Find_Son(1); fa[1] = 1;
	Find_Father(1);
	dfs(1, 1);
}
void Read() {
	int A, B;
	scanf("%d", &n);
	for(int i = 1; i < n; i++) {
		scanf("%d %d", &A, &B);
		a[B].push_back(A);
		a[A].push_back(B);
	}
	for(int i = 1; i <= n; i++)
		flag[i] = 1;
}
void DP(int now) {
	dp[now] = 1;
	for(int i = 0; i < v[now].size(); i++) {
		DP(v[now][i]);
		dp[now] += dp[v[now][i]];
		if(dp[v[now][i]] > n / 2)
			flag[now] = 0;
	}
	if(n - dp[now] > n / 2)
		flag[now] = 0;
}