樹形DP(鄰接表)

前言

本篇的程式碼均是由鄰接表來進行儲存，大概在還會再來一個用鏈式前向星版的吧~ （下次一定）

ps: 筆者已經很用心的在打$LaTeX$了，但還是不夠規範，望路過的大巨佬們多多指正

概念

度娘說

樹形動態規劃問題可以分解成若干相互聯絡的階段，在每一個階段都要做出決策，全部過程的決策是一個決策序列。要使整個活動的總體效果達到最優的問題，稱為多階段決策問題。

感覺好像並不明白她在說什麼
其實筆者個人理解，樹形DP更像是記憶化搜尋，各個節點都像樹一樣連線著。（無環圖）樹形DP顧名思義就是像樹一樣的DP，在有n個節點的時候，有n-1條邊連線著。
such as this

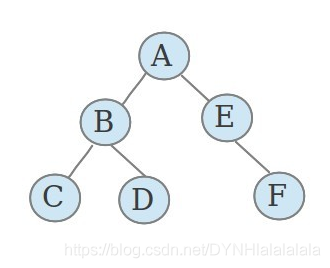
在解決樹形DP的問題時，我們通常以節點從深至淺作為階段，同時以遞回來實現。就像後序遍歷一樣。

那麼樹形DP有什麼作用呢？下面引出三種最版的題（也是今天筆者將要在本篇中寫的）。

• 最大獨立子集
• 樹的重心
• 樹的直徑

最大獨立子集

什麼是最大獨立子集呢？讓我們來引出一道題來看看。

沒有上司的晚會

題目描述

Ural大學有N個職員，編號為1~N。他們有從屬關係，也就是說他們的關係就像一棵以校長為根的樹，父結點就是子結點的直接上司。每個職員有一個快樂指數。現在有個週年慶宴會，要求與會職員的快樂指數最大。但是，沒有職員願和直接上司一起參加宴會。

輸入格式

第一行一個整數N。(1≤N≤6000)

接下來N行，第i+1行表示i號職員的快樂指數Ri。(-128≤Ri≤127)

接下來N-1行，每行輸入一對整數L,K。表示K是L的直接上司。

最後一行輸入0,0。

輸出格式

第1行：輸出最大的快樂指數。

樣例

樣例輸入
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
樣例輸出
5

從上題中我們就可以看見，對於每個節點，如果選中了它，就不可能選它的父親節點和兒子節點。那麼對於每一個節點我們就有了兩種狀態，選與不選。
設第i個為$dp[i]$， $dp[i][1]$表示選它自己$dp[i][0]$表示不選它自己
那麼狀態轉移方程就顯而易見了

$dp[i][0]=\sum ma{x}_{(}dp[j][0],dp[j][1])———j\in son(i)$
$dp[i][1]=\sum dp[j][0]———j\in son(i)$

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 6005;
int n;
int h[maxn];
int flag[maxn];
vector<int> a[maxn];
int dp[maxn][2];

void tree_dp(int x){
	dp[x][1] = h[x];
	dp[x][0] = 0;
	for(int i = 0; i < a[x].size(); i ++){
		int y = a[x][i];
		tree_dp(y);
		dp[x][0] += max(dp[y][1], dp[y][0]);
		dp[x][1] += dp[y][0]; 
	}
}
int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++){
		scanf("%d", &h[i]);
	}
	for(int i = 1; i < n; i ++){
		int x, y;
		scanf("%d %d", &x, &y);
		flag[x] = 1;
		a[y].push_back(x);
	}
	int root;
	for(int i = 1; i <= n; i ++){
		if(!flag[i]){
			root = i;
			break;
		}
	}
	tree_dp(root);
	printf("%d", max(dp[root][0], dp[root][1]));
	return 0;
}

樹的重心

重心是指地球對物體中每一微小部分引力的合力作用點。物體的每一微小部分都受地心引力作用(見萬有引力)，這些引力可近似地看成為相交於地心的匯交力系。由於物體的尺寸遠小於地球半徑，所以可近似地把作用在一般物體上的引力視為平行力系，物體的總重量就是這些引力的合力 。

不好意思這是物理

數學上的重心是指三角形的三條中線的交點，其證明定理有燕尾定理或塞瓦定理，應用定理有梅涅勞斯定理、塞瓦定理。

這才對嘛（以上兩條皆來自於百度百科）
在樹中的重心是指，去掉該點後，獨立子樹的節點個數最大的最小

以題舉例

求樹的重心

題目描述

樹的重心定義為樹的某個節點，當去掉該節點後，樹的各個連通分量中，節點數最多的連通分量其節點數達到最小值。樹可能存在多個重心。如下圖,當去掉點1後，樹將分成兩個連通塊：（2,4,5），（3,6,7），則最大的連通塊包含節點個數為3。若去掉點2，則樹將分成3個部分，（4），（5），（1,3,6,7）最大的連通塊包含4個節點；第一種方法可以得到更小的最大聯通分量。可以發現，其他方案不可能得到比3更小的值了。所以，點1是樹的重心。

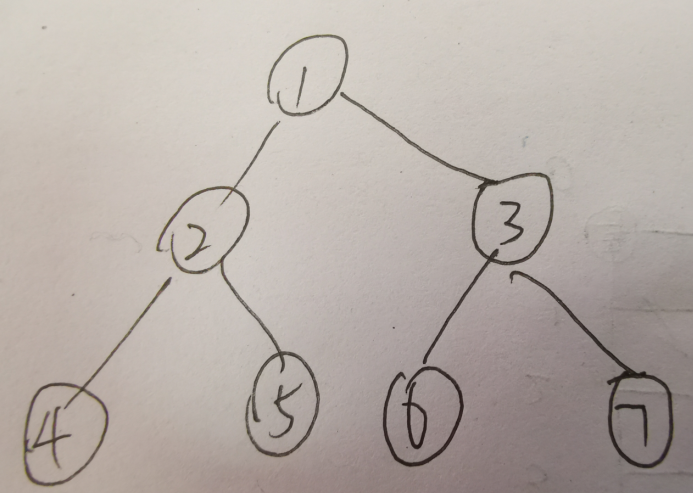
輸入格式

輸入：第一行一個整數n，表示樹的結點個數。（n<100）

接下來n-1行，每行兩個數i，j。表示i和j有邊相連。

輸出格式

輸出：第一行一個整數k，表示重心的個數。

接下來K行，每行一個整數，表示重心。按從小到大的順序給出。

樣例

樣例輸入
7
1 2
1 3
2 4
2 5
3 6
3 7
樣例輸出
1
1

其實解決這個問題，我們只需要知道與每個點的子樹的節點數，通過"刪除重心後所得的所有子樹，節點數不超過原樹的 $\frac{1}{2}$，一棵樹最多有兩個重心，且相鄰。"這一性質來找到重心。
（上面的這一性質其實很好證明（並不嚴謹，只是為了方便理解），因為我們除了鏈的根與葉子以外都有至少兩個度，如果刪除重心後所得的所有子樹，節點數超過原樹的 $\frac{1}{2}$， 那麼為什麼不能選取該子樹的節點為重心呢， 如果原有奇數個點，找到最中間的即可，原有偶數個節點，取其節點數/2的向上，向下取整都可以為為重心）

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 105;

int Max(int x, int y){
	return x > y ? x : y;
}

int Min(int x, int y){
	return x < y ? x : y;
} 

struct node{
	int x, f;
}; 
int n;
vector<int> a[maxn];
int siz[maxn], vis[maxn];
int nimsum = 0x3f3f3f3f;
int ans[maxn];
int cnt;

void dfs(int x, int f){
	bool flag;
	flag = 1;
	siz[x] = 1;
	for(int i = 0; i < a[x].size(); i ++){
		int y = a[x][i];
		if(!vis[y]){
			vis[y] = 1;
			dfs(y, x);
			siz[x] += siz[y];
			if(siz[y] > n / 2){
				flag = 0;
			}
		}
	}
	if(n - siz[x] > n / 2){
		flag = 0;
	}
	if(flag){
		cnt ++;
		ans[cnt] =  x;
	}
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i < n; i ++){
		int x, y;
		scanf("%d %d", &x, &y);
		a[x].push_back(y);
		a[y].push_back(x);
	}
	vis[1] = 1;
	dfs(1, -1);
	sort(ans + 1, ans + cnt + 1);
	printf("%d\n", cnt);
	for(int i = 1; i <= cnt; i ++){
		printf("%d\n", ans[i]);
	}
	return 0;
}

筆者在做這道題時，將flag定義在了全域性，以至於只能輸出0。
因為在子節點不為重心時，flag會為0，但回溯之後flag還是0，但其父節點卻有可能是重心，這樣就會找不到重心，以至於只能輸出0（如下圖）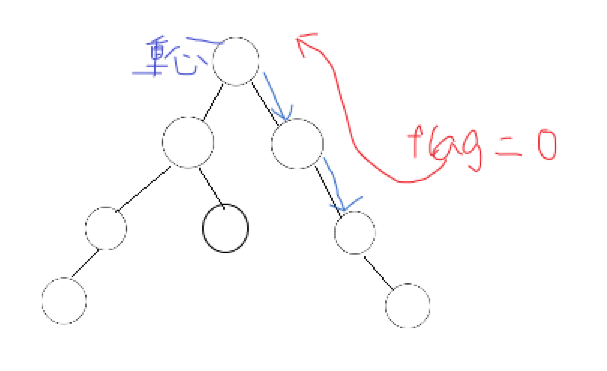

樹的直徑

題目描述

給定一個有個節點的樹，樹以個點條邊的無向圖形式給出， 求樹的直徑。

輸入格式

輸入的第1行為包含了一個正整數，為這棵二元樹的結點數。

接下來N行，每行有個正整數，表示有一條從到的無向邊。

輸出格式

輸出包括1個正整數，為這棵二元樹的直徑。

樣例

樣例輸入
10
1 2
1 3
2 4
4 5
4 6
1 7
5 8
7 9
7 10
樣例輸出
6

直徑我們都知道是啥，那什麼是樹的直徑呢？就是樹上兩點距離的最大值(做題思路在程式碼下)

#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
const int maxn = 1e6 + 5;

int n;
vector<int> a[maxn];
int ans[maxn];
int d[maxn];
bool vis[maxn];

void dfs(int x){
	vis[x] = 1;
	for(int i = 0; i < a[x].size(); i ++){
		int y = a[x][i];
		if(!vis[y]){
			dfs(y);
			ans[x] = max(ans[x], d[x] + d[y] + 1);
			d[x] = max(d[x], d[y] + 1);
		}
	}
}
int main() {
	scanf("%d", &n);
	for(int i = 1; i < n; i ++){
		int x, y;
		scanf("%d %d", &x, &y);
		a[x].push_back(y);
		a[y].push_back(x);
	} 
	int an = 0;
	dfs(1);
	for(int i = 1; i <= n; i ++){
		an = max(an, ans[i]);
	}
	printf("%d", an);
	return 0;
}

$d[x]$表示目前遍歷到的距離x最遠的鏈，$ans[x]$表示經過x點目前最長的鏈

那麼

ans[x] = max(ans[x], d[x] + d[y] + 1)

是什麼意思呢？
讓我們聯絡一下

$ans[x]$表示經過x點目前最長的鏈

因為$d[x]$表示目前遍歷到的距離x最遠的鏈，如果$d[y]$為次長的鏈。則沒有問題。如果$d[y]$為最長的鏈，要麼d[x]為次長鏈要麼在之後的$d[y]$為次長鏈。
所以上述做法是成立的~~

結語

筆者應該很快就會寫出鏈式前向星版的樹形DP，總之下次一定~