【資料結構與演演算法】之柱狀圖中最大矩形的演演算法
2020-10-05 12:01:08
一、題目要求
給定 n 個非負整數,用來表示柱狀圖中各個柱子的高度,並且每個柱子彼此相鄰,且寬度為 1 。求在該柱狀圖中,能夠勾勒出來的矩形的最大面積。
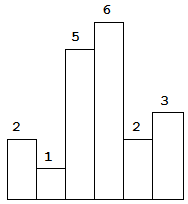
- 以下是柱狀圖的範例,其中每個柱子的寬度為 1,給定的高度為 [2,1,5,6,2,3]。
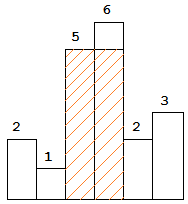
- 圖中陰影部分為所能勾勒出的最大矩形面積,其面積為 10 個單位。如下:
- 範例:
輸入: [2,1,5,6,2,3]
輸出: 10
二、範例演演算法
- 解題思路
- 為什麼要找左右兩邊高度大於當前遍歷的高度的下標?因為只有高度大於當前高度,面積才有可能更大,如果找<=的,面積只可能小於或者等於原先計算的最大面積。
- 為什麼單調增棧要儲存下標,而不是高度?因為通過下標可以找高度,而且通過下標是唯一的,這樣才能找到對應位置的對應高度。
- 進入外層迴圈,向右延伸,是確定了高度大於當前高度的最右下標。
- 進入內層迴圈,由於單調增棧的特性,棧pop出來的的一定是高度大於當前高度的最左下標。
- area =((外層迴圈的下標-1)-(內層迴圈走到的下標))* 內層迴圈pop出來的高度,然後取最大值。
- 陣列頭尾加入0,當作哨兵,所以一定會找到比當前index的高度還小的值,結束左右尋找的流程。
- 暴力解法(Swift),O(n2) 會超出時間限制:
func largestRectangleArea(_ heights: [Int]) -> Int {
if heights.count == 0 { return 0 }
var maxArea: Int = 0
for (index, height) in heights.enumerated() {
if height <= 0 { continue }
var curMax: Int = height
// 向左延伸,找到高度大於等於當前index的最小下標
for leftIndex in (0..<index).reversed() {
if heights[leftIndex] >= height {
curMax = curMax + height
} else {
break
}
}
// 向右延伸,找到高度大於等於當前index的最大下標
if index < heights.count-1 {
for rightIndex in (index+1)..<heights.count {
if heights[rightIndex] >= height {
curMax = curMax + height
} else {
break
}
}
}
maxArea = max(curMax, maxArea)
}
return maxArea
}
- 單調增棧(Swift)
func largestRectangleArea(_ heights: [Int]) -> Int {
var heights = [0] + heights + [0]
var maxArea: Int = 0
var stack: [Int] = []
for (index, height) in heights.enumerated() {
while !stack.isEmpty && stack.last != nil && heights[stack.last!] > height {
let removed = stack.removeLast()
if let leftEdge = stack.last {
var rightEdge = index
maxArea = max(maxArea, heights[removed] * (rightEdge - 1 - leftEdge))
}
}
stack.append(index)
}
return maxArea
}
- C 單調棧的演演算法實現
typedef struct {
void **data;
int top;
int size;
} Stack;
Stack *StackCreate(int stackSize) {
Stack *stack = (Stack *)malloc(sizeof(Stack));
if (stack == NULL) {
return NULL;
}
stack->data = (void **)malloc(sizeof(void **) * (stackSize + 1));
memset(stack->data, 0, sizeof(void **) * (stackSize + 1));
stack->top = -1;
stack->size = stackSize;
return stack;
}
void StackFree(Stack *obj) {
if (obj->data != NULL) {
free(obj->data);
obj->data = NULL;
}
free(obj);
obj = NULL;
return;
}
bool IsStackEmpty(Stack *obj) {
return (obj->top == -1);
}
bool IsStackFull(Stack *obj) {
return (obj->top == obj->size);
}
// 泛型介面,使用void *
void StackPush(Stack *obj, void *data) {
if (IsStackFull(obj) == true) {
return;
}
int top = obj->top;
obj->data[++top] = data;
obj->top = top;
return;
}
void StackPop(Stack *obj) {
if (IsStackEmpty(obj) == true) {
return;
}
void *data = obj->data[obj->top];
if (data != NULL) {
free(data);
data = NULL;
}
obj->top--;
return;
}
void *StackTop(Stack *obj) {
if (IsStackEmpty(obj) == true) {
return NULL;
}
return (obj->data[obj->top]);
}
void StackClear(Stack *obj) {
if (IsStackEmpty(obj) == true) {
return;
}
for (int i = 0; i <= obj->top; i++) {
void *data = obj->data[i];
if (data != NULL) {
free(data);
data = NULL;
}
}
obj->top = -1;
return;
}
void StackPushInt(Stack *obj, int value) {
int *node = (int *)malloc(sizeof(int));
*node = value;
StackPush(obj, node);
return;
}
int StackTopInt(Stack *obj) {
if (IsStackEmpty(obj) == true) {
return -1;
}
return *(int *)(obj->data[obj->top]);
}
void StackPushStr(Stack *obj, char *str, int strSize) {
char *node = (char *)malloc(sizeof(char) * (strSize + 1));
memcpy(node, str, strSize);
node[strSize] = '\0';
StackPush(obj, node);
return;
}
char *StackTopStr(Stack *obj) {
if (IsStackEmpty(obj) == true) {
return NULL;
}
return (char *)(obj->data[obj->top]);
}
#define MAX(a, b) ((a) > (b) ? (a) : (b))
int largestRectangleArea(int* heights, int heightsSize) {
int *data = (int *)malloc(sizeof(int) * (heightsSize + 1));
memcpy(data, heights, sizeof(int) * heightsSize);
data[heightsSize] = 0;
Stack *monotoneStack = StackCreate(heightsSize + 1);
int ret = 0;
for (int i = 0; i <= heightsSize; i++) {
int top = StackTopInt(monotoneStack);
while ((IsStackEmpty(monotoneStack) != true) && (data[top] >= data[i])) {
int h = data[top];
StackPop(monotoneStack);
top = StackTopInt(monotoneStack);
int sidx = top;
ret = MAX(ret, (h * (i - sidx - 1)));
}
StackPushInt(monotoneStack, i);
}
StackFree(monotoneStack);
return ret;
}
三、單調棧的理解(C++為例)
① 定義
- 定義:棧內元素保持有序的狀態的棧稱為單調棧,如下圖所示:
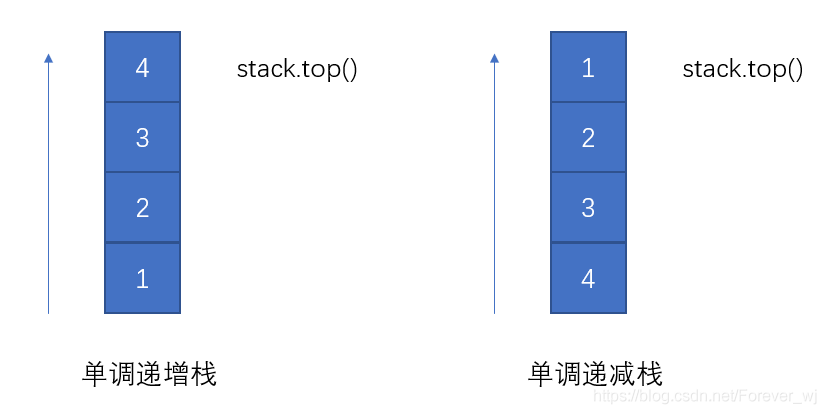
- 單調棧是一個定義簡單但應用起來比較複雜的資料結構,其根本應用可以概括為:在一個一維陣列中,幫助我們找到某個元素的左側或右側第一個大於或小於該元素的數。
- 具體來說,我們會維護一個單調棧(遞增或遞減視要求而定),這個棧在滿足一定情況時會將棧頂元素出棧(pop),一旦這種情況發生,那麼一定是遇到了我們要找的大於(或小於)該棧頂元素的數,相應的,我們應該在此時進行一系列的操作,得到我們想要的結果。核心在於如何正確理解出棧的含義。
② 佇列中數帽子問題
- 現有一條排好的隊伍,從隊首到隊尾,隊員們都戴著帽子,身高是無序的。假設每個人能看到隊伍中在他前面的比他個子矮的人的帽子,(如果出現一個比這個人個子高的人擋住視線,那麼此人不能看到高個子前面的任何人的帽子)現在請計算出這個隊伍中一共可以看到多少個帽子?例如給定陣列為:[2,1,5,6,2,3](順序為從隊尾到隊首)。如下所示:
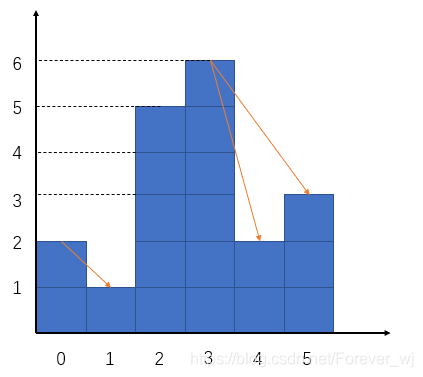
- 分析上圖可以得出,答案為3。從暴力角度嘗試去解這道題,顯然可以做到。對於陣列中每個元素,向右去找所有比它小的元素(找第第一個比它大的元素),這樣總的時間複雜度為O(n^2),最壞情況是這是一個單調遞減陣列,每次都要向右找到陣列的最末尾。顯然這不是理想的解法,我們可以應用單調棧來解決這個問題。其程式碼如下:
int countHats(vector<int>& heights) {
heights.push_back(INT_MAX);
stack<int> stk;
int sum = 0;
for(int i=0; i<heights.size(); i++) {
while( !stk.empty() && heights[i] > heights[stk.top()]) ) {
int top = stk.top();
stk.pop();
sum += i – top – 1;
}
stk.push(i);
}
return sum;
}
- 分析以上程式碼:
- 在以上程式碼中,我們維護了一個單調遞減棧,在棧中的元素都是單調遞減的,這表明棧內的元素還可能看到比它更小的元素(帽子)。
- 當遇到一個比棧頂元素大的元素時,說明棧頂元素不可能看到比它更小的元素了(因為遮擋作用),這時將棧頂元素pop出來,同時更新sum的值,sum += i – top – 1,表示棧頂元素與這個新元素間的距離,也就是棧頂元素能看到的最多的帽子數。
- 在for迴圈中,每個元素都會入棧和出棧,在出棧過程中總會計算出棧頂元素能看到的最多的帽子數,並更新sum值,當整個佇列迴圈結束後,得到的sum值就是最後隊伍中能看到的帽子總數。
- 注意為了使所有元素都能出棧(糟糕情況是單調遞減數列,這時似乎一次出棧都沒有發生,原因是最後一個元素後面不可能有新的元素出現了,但單調棧還在期待新的元素出現,為了反映元素不再出現這一事實,我們假設最後一個元素後面出現了一個無窮大的元素),即heights.push_back(INT_MAX)。
③ 尋找第一個比自己大的數
- 給一個陣列,返回一個大小相同的陣列。返回的陣列的第i個位置的值應當是,對於原陣列中的第i個元素,至少往右走多少步,才能遇到一個比自己大的元素(如果之後沒有比自己大的元素,或者已經是最後一個元素,則在返回陣列的對應位置放上-1)。
- 例如給定陣列為:[2,1,5,6,2,3],返回陣列應該為:[2,1,1,-1,1,-1]。
- 其實這個問題本質上和數帽子問題是一樣的,本質都是找到元素右邊第一個比它大的數,程式碼稍作改動即可。
int countSteps(vector<int>& heights) {
stack<int> stk;
vector<int> results(heights.size(), -1);
for(int i=0; i<heights.size(); i++) {
while( !stk.empty() && heights[i] > heights[stk.top()]) ) {
results[stk.top()] = i – stk.top();
stk.pop();
}
stk.push(i);
}
return results;
}
④ 最大矩形面積問題
- 給定 n 個非負整數,用來表示柱狀圖中各個柱子的高度。每個柱子彼此相鄰,且寬度為 1 。求在該柱狀圖中,能夠勾勒出來的矩形的最大面積。
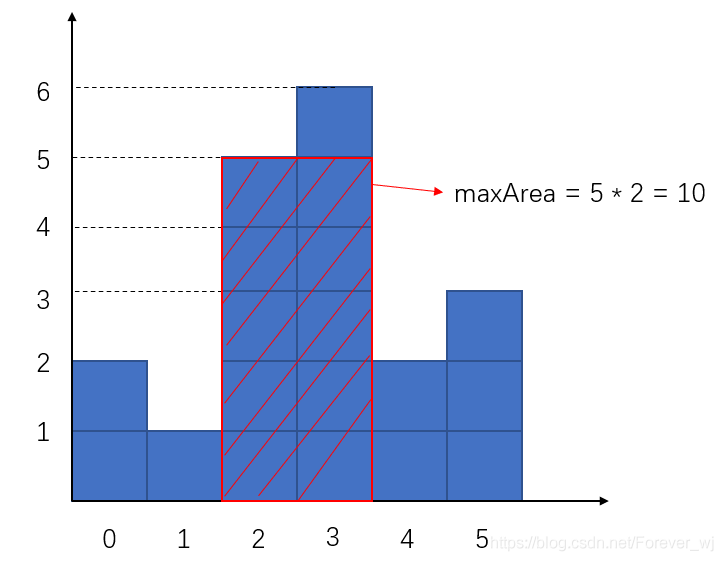
- 如上圖,矩形最大面積為10。這個問題同樣可以藉助單調棧來解決。在這之前,需要理解如何找到這個最大面積矩形,這個矩形的限制條件有兩個,一個是高度(也即組成矩形的最短的那根柱子高度),一個是寬度,(也即組成矩形的柱子個數)。
- 為了找到這個全域性最大值,我們遍歷所有區域性最優情況。那麼什麼是區域性最優解呢?我們將每個柱子的高度作為包含它的矩形的高度,也即這個柱子一定是這個矩形中最低的一個柱子,那麼我們下一步是求解這個矩形的寬度,顯然我們只需找到這個柱子左邊,右邊第一個比它低的柱子,就可以求出寬度。這顯然讓我們想到使用單調棧的資料結構,程式碼如下:
int largestRectangleArea(vector<int> heights) {
int maxArea = 0;
heights.push_back(0);
// monotone stack(ascending)
stack<int> stk;
for(int i = 0; i < heights.size(); i++) {
while(!stk.empty() && heights[i] < heights[stk.top()]) {
int top = stk.top();
// find the smaller element to the left of the current element
stk.pop();
maxArea = max(maxArea,heights[top]*(stk.empty() ? i : (i - stk.top()-1)));
}
stk.push(i);
}
return maxArea;
}
- 我們維護一個單調遞增棧,當遇到一個新元素小於棧頂元素時,發生出棧行為,表示棧頂元素向右遇到了第一個小於它的元素,同時在棧內的棧頂元素的下面一個元素即是棧頂元素向左尋找時第一個小於它的元素(這一點的原因值得仔細思考,其實是因為棧頂元素與其下面的元素間在原陣列中或許存在很多的元素,但它們必然是比棧頂元素大且比棧頂元素下面的元素小的,它們都在之前被彈出了棧)。
- 在出棧行為發生後,我們需要計算以棧頂元素的高度值作為矩形高度時的矩形面積,而矩形寬度已經可以計算了,因為我們找到了棧頂元素左右兩側小於它的第一個元素,於是區域性最優解得到計算。在整個迴圈中,所有元素進棧一次,出棧一次,時間複雜度為O(n)。
- 我們考慮本題中的第4號柱子作為棧頂元素時會發生的情況: