論文連結：https://arxiv.org/pdf/1710.10196.pdf

---

前言

這是一種針對GANs的訓練優化方法，從低解析度影象開始，通過向網路新增層來逐步提高解析度，如圖1。這種遞增的特性允許訓練首先發現影象分佈的大尺度結構，然後將注意力轉移到越來越細的尺度細節上，而不必同時學習所有的尺度。
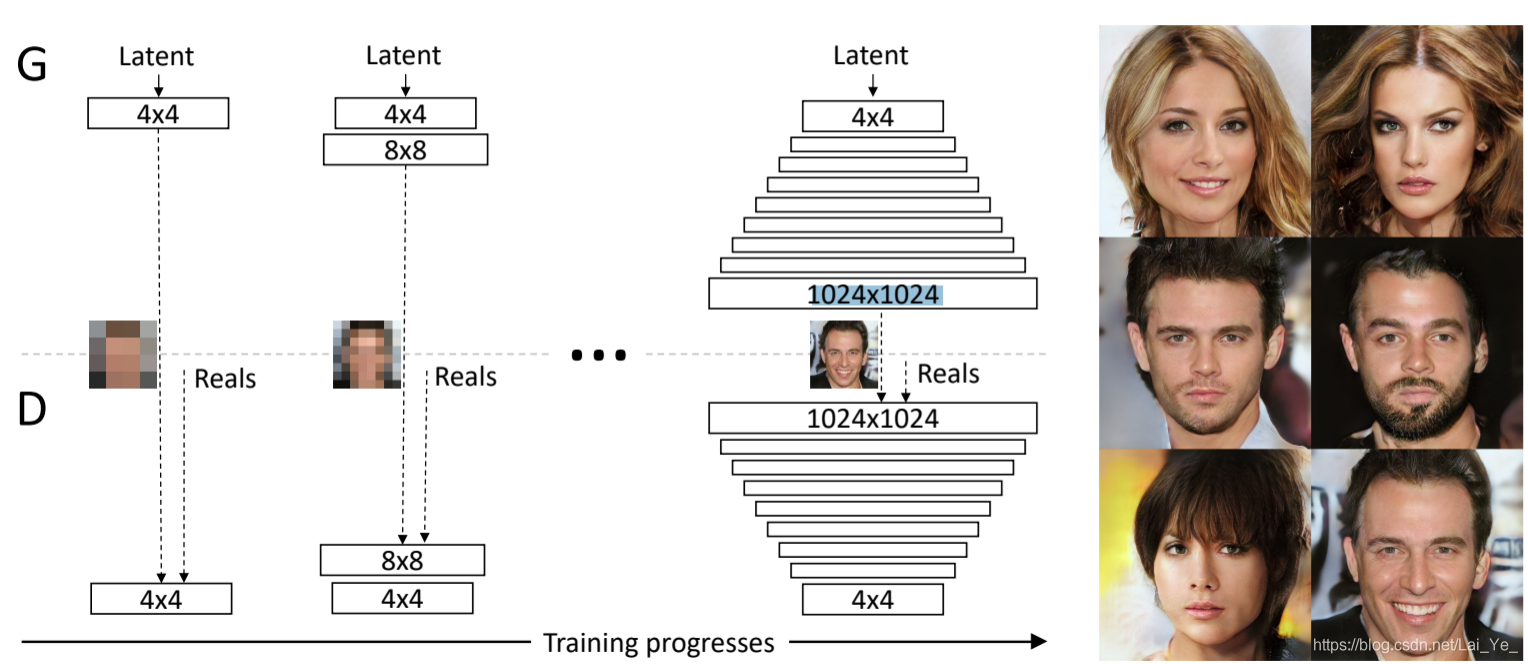圖1: 初始訓練時，生成器(G)和鑑別器(D)的空間解析度都很低，即4x4畫素。隨著訓練的進行，我們逐漸在G和D上增加層，從而提高了生成影象的空間解析度。在整個過程中，所有現有層都是可訓練的。這裡N x N是指在N x N空間解析度下的折積層。這允許在高解析度下穩定的擬合，也能夠極大地加快訓練速度。右邊展示了使用漸進式增長生成的6個1024 x 1024畫素範例影象。

---

我們使用生成器和鑑別器網路，它們彼此映象，同步發展。在整個訓練過程中，兩個網路中的所有現有層在訓練階段都是可訓練的。當新層被新增到網路中時，我們平滑地淡出現有網路，如圖2所示，這避免了對已經訓練良好的小解析度層的突然衝擊。
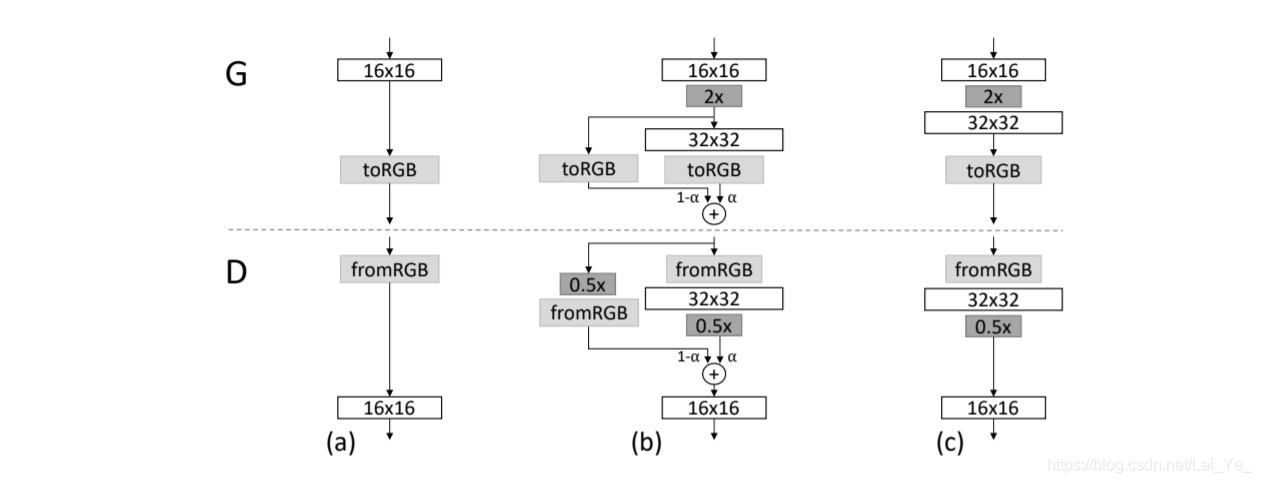圖2:當加倍生成器(G)和鑑別器(D)的解析度時，我們「平滑」地新增新圖層。該例子說明了從16×16影象$(a)$到32×32影象$(c)$的轉換過程。在轉換$(b)$過程中，我們將操作在更高解析度上的層類似殘差塊一樣處理，其權重$a$從0到1線性增加。這裡$2x$和$0.5x$分別表示使用最鄰近鄰濾波和平均池化將影象解析度加倍和減半。$toRGB$表示將特徵向量投影到RGB顏色層，$fromRGB$做相反操作; 都使用1 x 1折積。在訓練鑑別器時，我們輸入經過縮小的真實影象，以匹配當前網路的解析度。在解析度轉換期間，類似於生成器輸出組合兩種解析度的方式，我們在真實影象的兩種解析度之間插入。

---

漸進式訓練有幾個好處。
在早期，由於類別資訊和模式較少，小影象的生成實質上更穩定(Odena et al.，2017)：通過一點一點地提高解析度，通過重複一個簡化問題，而非直接解決從隱向量直接找到1024${}^2$的影象。實際上，它穩定了訓練，使我們能夠使用WGAN-GP或者LSGANs (Gulrajani et al., 2017)損失可靠地合成百萬畫素級的影象 (Mao et al., 2016b)。

減少了訓練時間：隨著GANs的逐漸增長，大多數迭代過程都是在較低的解析度下完成的，根據最終輸出的解析度，一般可以快2-6倍地獲得相近結果品質。

逐步構建GANs的想法與Wang等人(2017)的工作有關，他們使用多種鑑別器對不同的空間解析度進行操作。Durugkar等(2016)同時使用一個生成器和多個鑑別器進行工作，而Ghosh等(2017)使用多個生成器和一個鑑別器來做相反model工作。分級GANs (Denton. 等，2015; Huang等，2016; Zhang等，2017)為一個影象金字塔的每一層定義一個生成器和鑑別器。這些方法建立在與我們的工作相同的觀察基礎上——從隱變數到高解析度影象的複雜對映通過逐步學習會更加容易——但關鍵的區別在於我們只著眼於單個GAN，而非它們的廣義結構體系。與早期自適應增長網路的研究相比，如GNG(Fritzke, 1995)和NeuroEvolution of Augmenting Topologies (NEAT)(Stanley & Mikkulainen, 2002)，它們無節制地增加網路，而我們只是逐步引入預置的層。在此意義上，我們的方法類似於自動編碼器的分層訓練(Bengio等人，2007)。

正文部分將描述一些tricks。

---

---

以下是本篇文章正文內容

---

一、基於 ‘批標準差’ 增加多樣性（INCREASING VARIATION USING MINIBATCH STANDARD DEVIATION）

由於GAN網路傾向於學習資料集的子分部，由此2016年Salimans提出‘minibatch discrimination’即‘批判別’作為解決方案。它們不僅從單個影象中更是在整個minibatch中計算特徵統計資料，從而激勵生成影象和訓練影象的minibatch顯示類似的統計資料或分佈。

這是通過在鑑別器的末尾新增一個minibatch層來實現的，該層將學習一個大型張量，該張量將輸入量啟用並對映到一組統計陣列中。在一個minibatch中，為每個範例生成一組單獨的統計資訊組，並將其拼接到層的輸出，以便鑑別器可以在內部使用統計資訊。我們大大簡化了這種方法，同時也改進了多樣性。

在簡化方案中既沒有可學習引數也沒有新的超引數。我們首先計算每個minibatch空間位置上每個特徵圖的標準差。然後，我們將這些估計值平均到所有特徵圖和空間位置，得到單一值。我們複製擴張該值，將其連線到所有空間位置，並覆蓋整個minibatch，從而產生一個額外的(常數)特徵圖。計算方法簡述如下：

   input:[N,H,W,fmaps]；獲取批大小s=nhwf.shape;
   (1) 先計算N個特徵圖的標準差得到特徵圖fmap1:[1,H,W,fmaps]
   (2) 對fmap1求均值，得到值M1:[1,1,1,1]
   (3) 複製擴張M1得到N個特徵圖fmap2:[N,H,W,1]
   (4) 將fmap2新增至每個樣本的特徵圖中

理論上，這一層可以插入到鑑別器的任何地方，但是我們發現最好是在接近微端插入。

二、歸一化處理生成器和鑑別器（NORMALIZATION IN GENERATOR AND DISCRIMINATOR）

由於兩種網路之間的不健康競爭，GANs傾向於訊號強度的升級。GANs的實際需要是限制訊號的大小和競爭。我們使用一種方法，它包含了兩個成分，而這兩個成分都不包含可學習引數。

PGGAN使用兩種不同的方式來限制梯度和不健康博弈，而且方法均採用非訓練的處理方式.

1. 平衡學習率（EQUALIZED LEARNING RATE）

使用簡單的$N(0,1)$初始化，然後在執行時顯式地縮放權重。詳細解釋就是：Initialization權重後設定$W_i=W_i/c$，其中$W_i$是權重，$c$是He的初始化方法的每層歸一化常數(He，2015)。

動態地進行而非在初始化做有些許好處，與常用的自適應隨機梯度下降方法（如RMSProp (Tieleman & Hinton, 2012)和Adam (Kingma & Ba, 2015)）中的尺度不變性有關。這些方法通過預估的標準差對梯度更新進行標準化，從而使更新不依賴於引數的尺度。如果某些引數的動態範圍比其他引數大，則需要更長的時間來調整。初始化導致的結果會使學習率過大或過小。我們的方法確保了動態範圍，因此學習速度對所有權值而言是相同的。

He的初始化方法能夠確保網路初始化的時候，隨機初始化的引數不會大幅度地改變輸入訊號的強度。然而PGGAN中不僅限初始狀態scale而是實時scale，其中He公式如下：

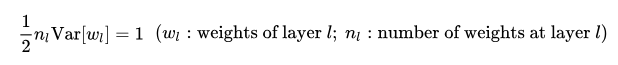
2. 生成器的畫素歸一化（PIXELWISE FEATURE VECTOR NORMALIZATION IN GENERATOR）

為了避免由於競爭導致生成器和鑑別器的大小交替失控的情況（生成器的梯度崩潰），我們在每個折積層之後將生成器中每個畫素的特徵向量歸一化為單位長度。我們使用一種變體的「區域性響應歸一化」(Krizhevsky，2012)來實現這一點。公式如下：
$$b_{x,y}=\frac{a_{x,y}}{\sqrt{\frac{1}{N}{\sum }_{j=0}^{N-1}(a_{x,y}^j{)}^2+ϵ}}$$其中：$ϵ=10^{-8}$,$N$是feature map的個數，$b_{x,y}$和$a_{x,y}$則分別是畫素$(x,y)$中的初始和歸一化特徵向量。

Pixel norm（畫素規範），它是local response normalization的變種。Pixel norm沿著channel維度做歸一化，這樣歸一化的一個好處在於，feature map的每個位置都具有單位長度。這個歸一化策略與作者設計的Generator輸出有較大關係，Generator的輸出層並沒有Tanh或者Sigmoid啟用函數。

---

三、構造漸增型網路（PROGRESSIVE NETWORK）

在遞增的訓練階段，生成器和判別器的型號也是在逐步拓展的，比如訓練128x128影象，我們從4x4開始訓練，訓練階段有：

stage 1 4x4 穩定 level2-net
stage 2 8x8 過渡 level3-net
stage 3 8x8 穩定 level3-net
stage 4 16x16 過渡 level4-net
stage 5 16x16 穩定 level4-net
stage 6 32x32 過渡 level5-net
stage 7 32x32 穩定 level5-net
stage 8 64x64 過渡 level6-net
stage 9 64x64 穩定 level6-net
stage 10 128x128 過渡 level7-net
stage 11 128x128 穩定 level7-net

生成器和鑑別器的網路架構主要由複製的3層塊組成，我們在訓練過程中逐一引入。生成器的最後一個Conv 1 x 1層對應於圖2中的toRGB，鑑別器的第一個Conv 1 x 1層對應於fromRGB。我們從4×4解析度開始訓練網路，直到鑑別器已經處理了規定數目的真實影象。然後在兩個階段交替進行: 在同數量影象組中在第一個3層塊中進行影象淡入處理，為這些影象中定網路，在接下來的3層塊中再進行淡入處理，以此類推。

我們的隱向量對應於512維超球面上的隨機點，並且我們在$[-1,1]$中表示訓練和生成的影象。除了最後一層使用線性啟用之外，我們在兩個網路的所有層中都使用 leakiness為0.2的leaky ReLU。在GANs的兩種網路中不使用批次處理歸一化、層歸一化或權值歸一化，但我們在生成器中每個Conv 3 x 3層之後對特徵向量進行畫素歸一化，如2.2節所述。我們根據帶有單位方差的正態分佈將所有的權值初始化，並將偏差引數初始化為0。在執行時，使用特定於層的常數來縮放權重，如2.1節所述。我們將跨小批（cross-minibatch）標準偏差作為4 x 4解析度的附加特徵圖加入鑑別器的末端，如第1節所述。

1. 上取樣（UPSAMPLE）和下取樣（DOWNSAMPLE）

論文中上取樣由近鄰插值方法，下取樣由平均池化方法實現。
同時在折積過程中，考慮到deconv會讓生成模型遭受checkerboard效應，PGGAN移除了deconv 方式，改用了conv + upsample。
以下論文給出的生成器和判別器中的折積塊：
生成器折積塊：

判別器折積塊：

2. 設計不同level的生成器和判別器 (level = log${}_2$(res), res:當前解析度)

GAN網路從最低解析度4x4慢慢向最高解析度1024x1024學習，其中G&D網路也是逐階段遞增的。 以生成器為例，描述生成器的不同階段的搭建方式：

（1）建立level=2的初始折積層

如圖構造了一個CONV4x4+CONV3x3的二級初始結構。

（2）建立拓撲折積層

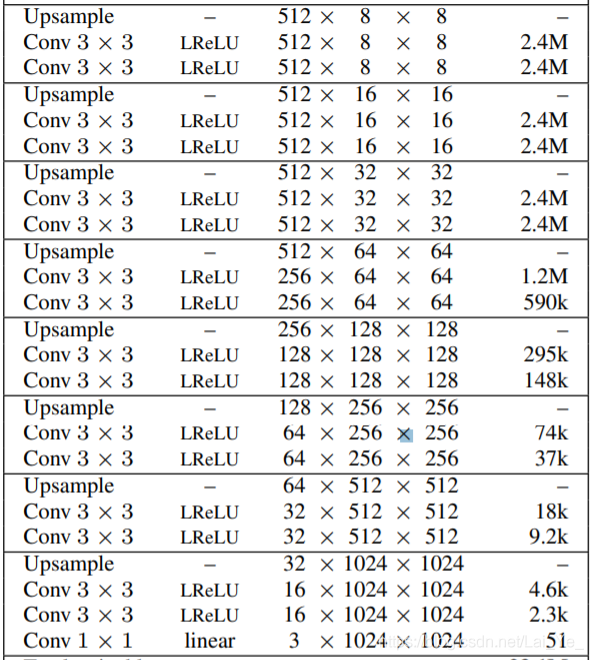網路拓撲結構如上圖，通過折積塊拼接成更高階網路，其中每個折積塊的特徵圖數量是指定的，PGGAN在論文裡指定為:
feats_map_num = [512,512,512,512,256,128,64,32,16]

（3）生成器輸出（整合特徵圖：toRGB）

經過多層折積之後，我們獲得了特徵圖，輸出端則需要將這些特徵圖整合為3通道的RGB影象，具體而言就是要構造一個toRGB函數，並考慮特徵圖整合過程中的過渡階段。

---

四、訓練設定（TRAINING CONFIGURATION）

1. Adam演演算法

在訓練網路時採用Adam優化演演算法 (Kingma & Ba, 2015) ：
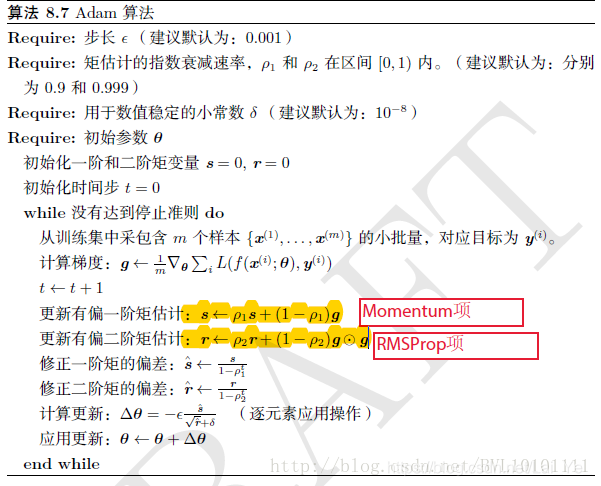從while迴圈往下看：
第一行是更新step，訓練集取樣，
第二行是計算梯度，
第三行計算一階矩的估計，即mean均值
第四行計算二階距的估計，即variance，是二階距的一種。
第五、六行則是對mean和var進行校正，因為mean和var的初始值為0，所以它們會向0偏置，這樣處理後會減少這種偏置影響。
第七行梯度下降。$ϵ$後的梯度是用一階距和二階距估計的。

由上圖演演算法顯示，Adam演演算法可描述為兩種隨機梯度下降擴充套件式的集合，即：

適應性梯度演演算法（AdaGrad）為每一個引數保留一個學習率以提升在稀疏梯度（即自然語言和計算機視覺問題）上的效能。

均方根傳播（RMSProp）基於權重梯度最近量級的均值為每一個引數適應性地保留學習率。這意味著演演算法在非穩態和線上問題上有很有優秀的效能。

按照吳恩達博士的理論分析，使用Adam演演算法，可以方便設定$ϵ$的同時，能夠起到天然退火（annealing）的效果。

論文中設定步長0.001，一階矩估計的指數衰減率0.9，二階矩估計的指數衰減率0.99，解析度10E-8。

2. mini_batch設定

為了節省記憶體預算，在解析度較大（$>=128^2$）的情況下逐次降低minibatch size，比如:
$4^2=128^2\backsim size=16$
$256^2\backsim size=14$
$512^2\backsim size=6$
$1024^2\backsim size=3$

3. Cost Function WGAN-GP

論文中使用了WGAN-GP loss（基於WGAN的改進函數模型，加入gradient penalty——一種聯絡了閾值K和原距離函數的loss function，它實現了將引數與限制聯絡起來達到真實的Lipschitz限制條件。），在此基礎上進行了進一步的改進，首先設定了$n_{critic}=1$，在每批樣本進行了生成器與鑑別器的交替訓練。此外，為了解決鑑別器的零漂問題，將loss修正入如下：
$$L^{\prime }=L+{ϵ}_{drift}{E}_{x\in P_r}[D(x{)}^2],{ϵ}_{drift}=1$$

---

五、生成結果的品質評價 – 多尺度統計相似度（ MULTI-SCALE STATISTICAL SIMILARITY）

總體思想：生成器可以基於所有尺度，產生區域性影象結構和訓練集是相似的樣例。通過收集和評估一些指示性指標，可以對結果影象進行一些比較可信的評價。

具體策略：從$16^2$畫素開始學習生成影象和目標影象的Laplacian金字塔（Burt＆Adelson，1987），並通過它表示區域性圖片匹配分佈的多尺度統計相似性，其中單個拉普拉斯金字塔等級對應於一個特定的空間頻帶。隨機取樣特定數目的結果影象，並從拉普拉斯Laplacian金字塔的每一級中提取描述符。在論文中每個描述符都是具有3個顏色通道的$7\times 7$的相鄰畫素點，記為$x\in R^{147}$。根據訓練集和生成集中的$l$級的patch匹配分別求得每個顏色通道的均值和標準差，然後通過計算它們的SWD（sliced Wasserstein distance）值來評估統計相似性。

---

總結

PGGAN在生成高解析度影象上具有著相當傑出的能力，而它在人臉影象生成上所展示的優良表現，是否說明它在資料擴充套件和場景生成領域同樣能夠提高其效能？這裡可以多做一些嘗試和研究。

---

參考：

https://blog.csdn.net/liujunru2013/article/details/78545882

https://blog.csdn.net/weixin_41024483/article/details/83116856

https://blog.csdn.net/u013412904/article/details/79045473

https://blog.csdn.net/u013139259/article/details/78885815