雙目結構光測量系統

顧名思義，雙目結構光就是採用兩個相機+投影儀的結構，兩個相機分別放置在投影儀的兩側。該系統測量原理首先採用投影儀投射設計的光柵編碼圖案到測量物件表面，然後被雙目相機同步採集，兩個相機分別對光柵影象做相位解包演演算法，利用相位資訊對雙目視覺進行匹配，然後通過雙目視覺的重建方式對測量物體重建三維點雲。

本部落格採用三頻外差的方法求解相位資訊，然後對雙目系統進行去除畸變、立體校正，利用相位對雙目進行對等匹配，然後三維重建點雲。

三頻外差光柵生成

三組頻率分別為76、57、37，76為高頻條紋的頻率，57為中頻條紋的頻率，37為低頻條紋的頻率。其中高頻的條紋設定為4步相移，中頻和低頻的分別設定為3步相移，具體的Matlab生成程式碼如下：

R = 1140;  C = 912;   % 光柵尺寸1140*912

P1 = 1140/76;        % 頻率76的光柵寬度
P2 = 1140/57;        % 頻率57的光柵寬度
P3 = 1140/37;        % 頻率37的光柵寬度

a = 126;           % 背景光強
b = 126;           % 調變光強

I0 = zeros(1140,912);   %定義影象尺寸大小
H1 = I0; H2 = I0; H3 = I0; H4 = I0;
H5 = I0; H6 = I0; H7 = I0; 
H8 = I0; H9 = I0; H10 = I0;

for i = 1:1140
    for j = 1:912
        H1(i,j) = a+b*cos(2*pi*(j-1)/P1);                %4步相移餘弦光柵 --高頻
        H2(i,j) = a+b*cos(2*pi*(j-1)/P1+1*2*pi/4);
        H3(i,j) = a+b*cos(2*pi*(j-1)/P1+2*2*pi/4);
        H4(i,j) = a+b*cos(2*pi*(j-1)/P1+3*2*pi/4);
        
        H5(i,j) = a+b*cos(2*pi*(j-1)/P2-2*pi/3);         %3步相移餘弦光柵 --中頻
        H6(i,j) = a+b*cos(2*pi*(j-1)/P2);
        H7(i,j) = a+b*cos(2*pi*(j-1)/P2+2*pi/3);
        
        H8(i,j) = a+b*cos(2*pi*(j-1)/P3-2*pi/3);         %3步相移餘弦光柵 --低頻
        H9(i,j) = a+b*cos(2*pi*(j-1)/P3);
        H10(i,j) = a+b*cos(2*pi*(j-1)/P3+2*pi/3);
 
    end
end 

%% ----------------------【光柵寫出】--------------------------

for k = 1:10
    eval(['H','=H',num2str(k),';']);
    H = uint8(H);
    img_name = ['gratings/',num2str(k),'.bmp'];
    imwrite(H,Himg_name);
end

三頻外差相位解包

每個頻率的光柵求出的相位都是包裹相位，其形式如同下式的 $\phi(x,y)$ 所示，這樣的相點陣圖不能直接用於雙目匹配，為了獲取絕對相位 $\Phi(x,y)$ ，我們需要獲取一個條紋階次 $k (x, y)$ ，然後通過下式將包裹相位展開為絕對相位：
$\Phi(x,y) = \phi(x,y) + 2\pi \times k(x,y)$
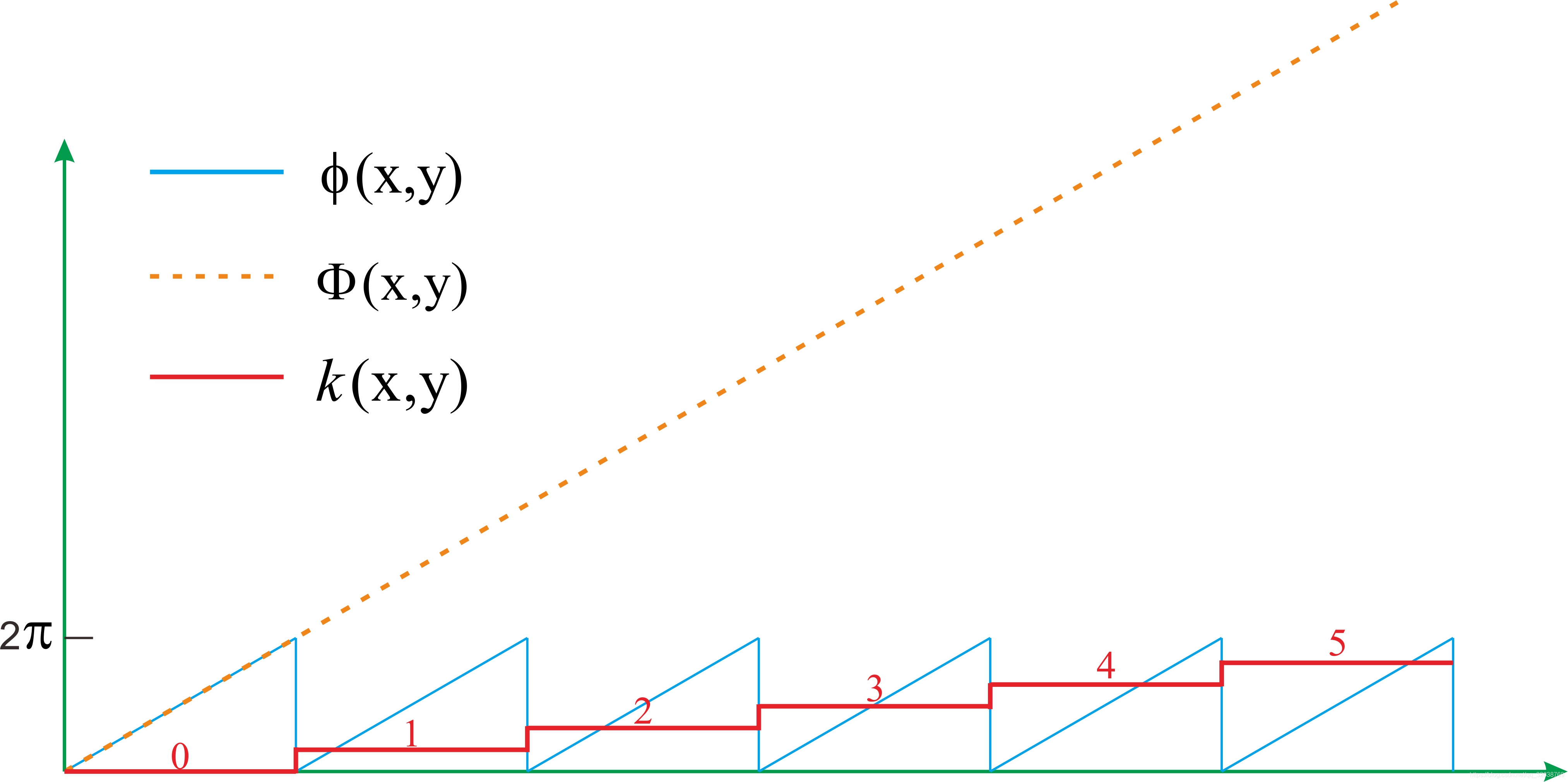
在這裡插入圖片描述
三頻外差的高頻條紋就是為了獲取包裹相位，這裡有人可能會問，為什麼其他頻率的不能當作包裹相位 $\phi(x,y)$ 呢，因為條紋頻率越高，訊雜比就越大，因此高頻的相位精度更好。中頻和低頻的光柵就是為了獲取 $k (x, y)$ 的，其具體獲取方式如下（matlab程式碼）：

% ----------------變數預定義
[R C] = size(H1);
phi1 = zeros(R,C);  phi2 = phi1;  phi3 = phi1;
k1 = phi1;  k2 =phi1;  k = phi1;
phi_eq2 = phi1; phi_eq1 = phi1;  phi_eq = phi1;
phase = phi1;
% ---------------高頻包裹相位phi1
phi1 = atan2(H4-H2,H1-H3);
phi1(phi1<0) = phi1(phi1<0)+2*pi;

% ---------------中頻包裹相位phi2
phi2 = atan2(sqrt(3)*(H5-H7),2*H6-H5-H7);
phi2(phi2<0) = phi2(phi2<0)+2*pi;

% ---------------低頻包裹相位phi3
phi3 = atan2(sqrt(3)*(H8-H10),2*H9-H8-H10);
phi3(phi3<0) = phi3(phi3<0)+2*pi;

% ---------------高頻-中頻外差相位phi_eq1
phi_eq1 = phi1-phi2;
phi_eq1(phi_eq1<0) = phi_eq1(phi_eq1<0)+2*pi;
% ---------------中頻-低頻外差相位phi_eq2
phi_eq2 = phi2-phi3;
phi_eq2(phi_eq2<0) = phi_eq2(phi_eq2<0)+2*pi;
% ---------------高頻-中頻-低頻外差相位phi_eq（三個頻率的綜合外差）
phi_eq =  phi_eq2-phi_eq1;
phi_eq(phi_eq<0) = phi_eq(phi_eq<0)+2*pi;

L_12 = p1*p2/(p2-p1);          % 外差相位phi_eq1波長
L_23 = p2*p3/(p3-p2);          % 外差相位phi_eq2波長
L_eq = L_23*L_12/(L_12-L_23);  % 外差相位phi_eq波長

k1 = round(((L_12/p1)*phi_eq1-phi1)/(2*pi));  
k2 = round(((L_eq/L_12)*phi_eq-phi_eq1)/(2*pi));
k = k2*(L_12./p1) + k1;

% -----------------------相位展開，得絕對相位phase---------------------------
phase = phi1 + k*2*pi;

實驗

投影儀投射光柵，被左右相機同時採集，然後通過上次的方式進行相位解包，進行雙目相機匹配和三維重建，然後獲取了三維點雲。

在這裡插入圖片描述
如需交流合作，可以聯絡qq：1091454117

雙目結構光的三維重建方法（相移法+多頻外差相位解包）（含相位程式碼）

雙目結構光測量系統

三頻外差光柵生成

三頻外差相位解包

實驗