藍橋杯第五屆省賽題目及題解
目錄
第一題:啤酒和飲料
啤酒每罐2.3元,飲料每罐1.9元。小明買了若干啤酒和飲料,一共花了82.3元。
我們還知道他買的啤酒比飲料的數量少,請你計算他買了幾罐啤酒。
注意:答案是一個整數。請通過瀏覽器提交答案。
不要書寫任何多餘的內容(例如:寫了飲料的數量,新增說明文字等)。
答案: 11 此時啤酒11罐,飲料30罐
#include<iostream>
using namespace std;
int main()
{
double beer, bev;//分別表示啤酒,飲料的錢
for (int i = 0; i < 50; i++)//啤機
{
for (int j = i; j < 50; j++)
{
beer = (double)i * 2.3;
bev = (double)j * 1.9;
if (beer + bev == 82.3)
{
cout << i << " " << j << endl;
system("pause");
return 0;
}
}
}
}第二題:切面條
一根高筋拉麵,中間切一刀,可以得到2根麵條。
如果先對摺1次,中間切一刀,可以得到3根麵條。
如果連續對摺2次,中間切一刀,可以得到5根麵條。
那麼,連續對摺10次,中間切一刀,會得到多少麵條呢?
答案是個整數,請通過瀏覽器提交答案。不要填寫任何多餘的內容。
分析:有點考空間思維能力啊,這個;需要自己畫圖理解。
答案:1024
第三題:李白打酒
話說大詩人李白,一生好飲。幸好他從不開車。
一天,他提著酒壺,從家裡出來,酒壺中有酒2鬥。他邊走邊唱:
無事街上走,提壺去打酒。
逢店加一倍,遇花喝一斗。
這一路上,他一共遇到店5次,遇到花10次,已知最後一次遇到的是花,他正好把酒喝光了。
請你計算李白遇到店和花的次序,可以把遇店記為a,遇花記為b。則:babaabbabbabbbb 就是合理的次序。像這樣的答案一共有多少呢?請你計算出所有可能方案的個數(包含題目給出的)。
注意:通過瀏覽器提交答案。答案是個整數。不要書寫任何多餘的內容。
dfs試探兩種情況
1.雨花喝一斗
2.遇店加一倍
當遇店的數等於5並且酒的剩餘為1,遇花的次數為9時,那麼方案數加一,否則return;
答案:14
#include<iostream>
using namespace std;
int ans;
void dfs(int beer, int dian, int hua)
{
if (beer == 1 && dian == 5 && hua == 9)
{
ans++;
return;
}
if (dian > 5 || hua > 9) return;
//1.遇花喝一斗
dfs(beer - 1, dian, hua + 1);
//2.遇店加一倍
dfs(2 * beer, dian + 1, hua);
}
int main()
{
dfs(2, 0, 0);
cout << ans << endl;
system("pause");
return 0;
}第四題:史豐收速算
史豐收速演演算法的革命性貢獻是:從高位算起,預測進位。不需要九九表,徹底顛覆了傳統手算!
速算的核心基礎是:1位數乘以多位數的乘法。
其中,乘以7是最複雜的,就以它為例。
因為,1/7 是個迴圈小數:0.142857...,如果多位數超過 142857...,就要進1
同理,2/7, 3/7, ... 6/7 也都是類似的迴圈小數,多位數超過 n/7,就要進n
下面的程式模擬了史豐收速演演算法中乘以7的運算過程。
乘以 7 的個位規律是:偶數乘以2,奇數乘以2再加5,都只取個位。
乘以 7 的進位規律是:
滿 142857... 進1,
滿 285714... 進2,
滿 428571... 進3,
滿 571428... 進4,
滿 714285... 進5,
滿 857142... 進6
請分析程式流程,填寫劃線部分缺少的程式碼。
//計算個位
int ge_wei(int a)
{
if(a % 2 == 0)
return (a * 2) % 10;
else
return (a * 2 + 5) % 10;
}
//計算進位
int jin_wei(char* p)
{
char* level[] = {
"142857",
"285714",
"428571",
"571428",
"714285",
"857142"
};
char buf[7];
buf[6] = '\0';
strncpy(buf,p,6);
int i;
for(i=5; i>=0; i--){
int r = strcmp(level[i], buf);
if(r<0) return i+1;
while(r==0){
p += 6;
strncpy(buf,p,6);
r = strcmp(level[i], buf);
if(r<0) return i+1;
______________________________; //填空
}
}
return 0;
}
//多位數乘以7
void f(char* s)
{
int head = jin_wei(s);
if(head > 0) printf("%d", head);
char* p = s;
while(*p){
int a = (*p-'0');
int x = (ge_wei(a) + jin_wei(p+1)) % 10;
printf("%d",x);
p++;
}
printf("\n");
}
int main()
{
f("428571428571");
f("34553834937543");
return 0;
}
注意:通過瀏覽器提交答案。只填寫缺少的內容,不要填寫任何多餘的內容(例如:說明性文字)
答案: if(r > 0) return i; //填空 (有點類似高進度乘法)
第五題:列印圖形
小明在X星球的城堡中發現瞭如下圖形和文字:
rank=3
*
* *
* *
* * * *
rank=5
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
ran=6
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
小明開動腦筋,編寫了如下的程式,實現該圖形的列印。
#define N 70
void f(char a[][N], int rank, int row, int col)
{
if(rank==1){
a[row][col] = '*';
return;
}
int w = 1;
int i;
for(i=0; i<rank-1; i++) w *= 2;
____________________________________________;
f(a, rank-1, row+w/2, col);
f(a, rank-1, row+w/2, col+w);
}
int main()
{
char a[N][N];
int i,j;
for(i=0;i<N;i++)
for(j=0;j<N;j++) a[i][j] = ' ';
f(a,6,0,0);
for(i=0; i<N; i++){
for(j=0; j<N; j++) printf("%c",a[i][j]);
printf("\n");
}
return 0;
}
請仔細分析程式邏輯,填寫缺失程式碼部分。
通過瀏覽器提交答案。注意不要填寫題目中已有的程式碼。也不要寫任何多餘內容(比如說明性的文字)
答案: f(a, rank - 1, row, col + w / 2);
#include<iostream>
using namespace std;
#define N 70
void f(char a[][N], int rank, int row, int col)
{
if(rank==1){
a[row][col] = '*';
return;
}
int w = 1;
int i;
for(i=0; i<rank-1; i++) w *= 2;
// ____________________________________________;
f(a, rank - 1, row, col + w / 2);//處理上面的三角新
f(a, rank-1, row+w/2, col);//處理左下角的三角形
f(a, rank-1, row+w/2, col+w);//處理右下角的三角形
}
int main()
{
char a[N][N];
int i,j;
for(i=0;i<N;i++)
for(j=0;j<N;j++) a[i][j] = ' ';
f(a,5,0,0);
for(i=0; i<N; i++){
for(j=0; j<N; j++) printf("%c",a[i][j]);
printf("\n");
}
return 0;
}
第六題:奇怪的分式
上小學的時候,小明經常自己發明新演演算法。一次,老師出的題目是:
1/4 乘以 8/5
小明居然把分子拼接在一起,分母拼接在一起,答案是:18/45 (參見圖1.png)

老師剛想批評他,轉念一想,這個答案湊巧也對啊,真是見鬼!
對於分子、分母都是 1~9 中的一位數的情況,還有哪些算式可以這樣計算呢?
請寫出所有不同算式的個數(包括題中舉例的)。
顯然,交換分子分母后,例如:4/1 乘以 5/8 是滿足要求的,這算做不同的算式。
但對於分子分母相同的情況,2/2 乘以 3/3 這樣的型別太多了,不在計數之列!
注意:答案是個整數(考慮對稱性,肯定是偶數)。請通過瀏覽器提交。不要書寫多餘的內容。
答案 14 記得要去重,要出去分子分母相同的情況
#include<iostream>
#include<algorithm>
using namespace std;
int gcd(int a, int b)
{
if(b == 0) return a;
return gcd(b, a %b);
}
int main()
{
int ans = 0;
int a, b, c, d;
for(a = 1; a <= 9; a++) //第一個分數的分子
for(b = 1; b <= 9; b++) //第一個分數的分母
for(c = 1; c <= 9; c++) //第二個分數的分子
for(d = 1; d <= 9; d++) //等二個分數的分母
{
int x1, y1, x2, y2; //分別就算兩種方法得到的新分數的分子分母
double res1, res2;
//基本的乘法產生的分數
x1 = a * c, y1 = b * d;
res1 = gcd(x1, y1);
x1 /= res1, y1 /= res1;
//拼接的方式計算
x2 = a * 10 + c, y2 = b * 10 + d;
res2 = gcd(x2, y2);
x2 /= res2, y2 /= res2;
if(x1 == x2 && y1 == y2 && a != b && c != d)
{
ans++;
cout << a << "/" << b << " " << c << "/" << d << endl;
}
}
cout << ans << endl;
return 0;
}
第七題:六角填數
如圖【1.png】所示六角形中,填入1~12的數位。
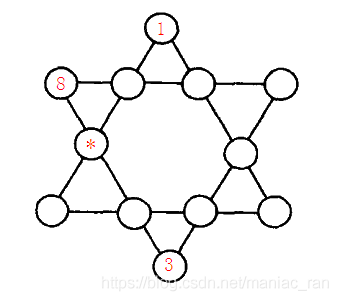
使得每條直線上的數位之和都相同。
圖中,已經替你填好了3個數位,請你計算星號位置所代表的數位是多少?
請通過瀏覽器提交答案,不要填寫多餘的內容。
分析:將剩餘的空白用陣列來填充,然後將剩下的數放到陣列中去,使用next_premutation產生全排列,然後check().
答案:10 每條橫線數位之和為26
#include<iostream>
#include<algorithm>
using namespace std;
bool check(int a[])
{
int res[6];
res[0] = 8 + a[0] + a[1] + a[2];
res[1] = 1 + a[0] + a[3] + a[5];
res[2] = 1 + a[1] + a[4] + a[8];
res[3] = 8 + a[3] + a[6] + 3;
res[4] = 3 + a[2] + a[4] + a[7];
res[5] = a[5] + a[6] + a[7] + a[8];
for(int i = 1; i < 6; i++)
{
if(res[i] != res[0]) return false;
}
return true;
}
int main()
{
int a[9] = { 2, 4, 5, 6, 7, 9, 10, 11, 12 };
do{
if(check(a))
{
for(int i = 0; i < 9; i++)
{
cout << i << " " << a[i] << endl;
}
return 0;
}
}while(next_permutation(a, a + 9));
}
第八題:螞蟻感冒
長100釐米的細長直杆子上有n只螞蟻。它們的頭有的朝左,有的朝右。
每隻螞蟻都只能沿著杆子向前爬,速度是1釐米/秒。
當兩隻螞蟻碰面時,它們會同時掉頭往相反的方向爬行。
這些螞蟻中,有1只螞蟻感冒了。並且在和其它螞蟻碰面時,會把感冒傳染給碰到的螞蟻。
請你計算,當所有螞蟻都爬離杆子時,有多少隻螞蟻患上了感冒。
【資料格式】
第一行輸入一個整數n (1 < n < 50), 表示螞蟻的總數。
接著的一行是n個用空格分開的整數 Xi (-100 < Xi < 100), Xi的絕對值,表示螞蟻離開杆子左邊端點的距離。正值表示頭朝右,負值表示頭朝左,資料中不會出現0值,也不會出現兩隻螞蟻佔用同一位置。其中,第一個資料代表的螞蟻感冒了。
要求輸出1個整數,表示最後感冒螞蟻的數目。
例如,輸入:
3
5 -2 8
程式應輸出:
1
再例如,輸入:
5
-10 8 -20 12 25
程式應輸出:
3
分析:這個題在網上看過講解,經常刷題的話,刷到過類似的題的話還是比較輕鬆;否則就看個能能力吧~~~。本題呢,先要判斷第一個感染螞蟻的朝向,然後所有的螞蟻都不考慮碰頭然後調換頭的朝向去看。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 55;
int n;
int a[N];
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i++) scanf("%d", &a[i]);
int ans = 1;
if(a[0] > 0)
{//第一隻感冒的螞蟻頭朝右
bool flag = false; //判斷是否
int res = 0; //記錄頭朝左並且距離到起點比a[0]小的螞蟻
for(int i = 1; i < n; i++)
{
if(a[i] > 0 && a[i] < a[0]) res++;
if(a[i] < 0 && -a[i] > a[0])
{
ans++;
flag = true;
}
}
if(flag == true) ans += res;
}
else
{//此時a[0] < 0 表示第一隻螞蟻頭朝左
bool flag = false;//判斷是否存在頭朝右且到原點的距離比a[0]小
int res = 0;
for(int i = 1; i < n; i++)
{
if(a[i] > 0 && a[i] < -a[0])
{
ans++;
flag = true;
}
if(a[i] < 0 && -a[i] > -a[0]) res++;
}
if(flag == true) ans += res;
}
printf("%d\n", ans);
return 0;
}
第九題:地宮取寶
X 國王有一個地宮寶庫。是 n x m 個格子的矩陣。每個格子放一件寶貝。每個寶貝貼著價值標籤。
地宮的入口在左上角,出口在右下角。
小明被帶到地宮的入口,國王要求他只能向右或向下行走。
走過某個格子時,如果那個格子中的寶貝價值比小明手中任意寶貝價值都大,小明就可以拿起它(當然,也可以不拿)。
當小明走到出口時,如果他手中的寶貝恰好是k件,則這些寶貝就可以送給小明。
請你幫小明算一算,在給定的局面下,他有多少種不同的行動方案能獲得這k件寶貝。
【資料格式】
輸入一行3個整數,用空格分開:n m k (1<=n,m<=50, 1<=k<=12)
接下來有 n 行資料,每行有 m 個整數 Ci (0<=Ci<=12)代表這個格子上的寶物的價值
要求輸出一個整數,表示正好取k個寶貝的行動方案數。該數位可能很大,輸出它對 1000000007 取模的結果。
例如,輸入:
2 2 2
1 2
2 1
程式應該輸出:
2
再例如,輸入:
2 3 2
1 2 3
2 1 5
程式應該輸出:
14
分析:dfs問題吧~~,可能還要考慮回溯的問題,需要記錄哪裡多少物品和每個物品的價值
這第一份程式碼只能通過28分的測試,僅僅供大家參考,這個是錯誤的!!!!我沒有測試用例,所以不知道錯在哪裡,求大佬提點分析~~~
#include<iostream>
using namespace std;
const int N = 1000000007;
const int M = 55;
int n, m, k;
int w[M][M];
long long ans;
void dfs(int r, int c, int cnt,int wmax)
{
if(r == n - 1 && c == m - 1)
{
if((w[r][c] > wmax && cnt == k - 1) || cnt == k)
{
ans++;
if(ans > N)
ans = ans % N;
}
return;
}
if(cnt > k) return;
//1.這個物品比小明手上的物品都大,並且小明選他
//這是小明是能向右或者向下走
if(r + 1 < n && w[r][c] > wmax) dfs(r + 1, c, cnt + 1, w[r][c]); //小明向下走並選這個物品
if(c + 1 < m && w[r][c] > wmax) dfs(r, c + 1, cnt + 1, w[r][c]); //小明向右走並選這個物品
//不管這個物品是否大於小明的所有的物品,小明都向右或向下走
if(r + 1 < n) dfs(r + 1, c, cnt, wmax); //小明向下走並選這個物品
if(c + 1 < m) dfs(r, c + 1, cnt, wmax); //小明向右走並選這個物品
}
int main()
{
//輸入
scanf("%d %d %d", &n, &m, &k);
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
scanf("%d", &w[i][j]);
}
}
//dfs去探測
dfs(0, 0, 0, 0);
cout << ans << endl;
return 0;
}下面的這份程式碼是在測評系統可以得滿分的。採用的是記憶搜尋,把每種狀態下的情況儲存起來,遇到已經出現的情況則返回。
#include<iostream>
#include<cstring>
using namespace std;
const int MOD = 1000000007;
int n, m, k;
int a[50][50];
long long cache[50][50][14][13];//儲存狀態
long long dfs(int x, int y, int max, int cnt)
{
if(cache[x][y][max + 1][cnt] != -1) return cache[x][y][max + 1][cnt];//如果這種轉態存在即返回
if(x == n || y == m || cnt > k) return 0;
long long ans = 0;
int cur = a[x][y];
if(x == n - 1 && y == m - 1)
{
if(cnt == k ||(cnt == k - 1 && cur > max))
{
ans++;
if(ans > MOD) ans %= MOD;
}
return ans;
}
if(cur > max)
{
ans += dfs(x + 1, y, cur, cnt + 1);
ans += dfs(x, y + 1, cur, cnt + 1);
}
//當該寶貝價值小於最大值或者大於不拿該寶貝的情況
ans += dfs(x + 1, y, max, cnt);
ans += dfs(x, y + 1, max, cnt);
//存狀態
cache[x][y][max + 1][cnt] = ans % MOD;
return ans % MOD;
}
int main()
{
scanf("%d %d %d", &n, &m, &k);
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
scanf("%d", &a[i][j]);
}
}
memset(cache, -1, sizeof(cache));
printf("%lld", dfs(0, 0, -1, 0));
return 0;
}
第十題:小朋友排隊
n 個小朋友站成一排。現在要把他們按身高從低到高的順序排列,但是每次只能交換位置相鄰的兩個小朋友。
每個小朋友都有一個不高興的程度。開始的時候,所有小朋友的不高興程度都是0。
如果某個小朋友第一次被要求交換,則他的不高興程度增加1,如果第二次要求他交換,則他的不高興程度增加2(即不高興程度為3),依次類推。當要求某個小朋友第k次交換時,他的不高興程度增加k。
請問,要讓所有小朋友按從低到高排隊,他們的不高興程度之和最小是多少。
如果有兩個小朋友身高一樣,則他們誰站在誰前面是沒有關係的。
【資料格式】
輸入的第一行包含一個整數n,表示小朋友的個數。
第二行包含 n 個整數 H1 H2 … Hn,分別表示每個小朋友的身高。
輸出一行,包含一個整數,表示小朋友的不高興程度和的最小值。
例如,輸入:
3
3 2 1
程式應該輸出:
9
【樣例說明】
首先交換身高為3和2的小朋友,再交換身高為3和1的小朋友,再交換身高為2和1的小朋友,每個小朋友的不高興程度都是3,總和為9。
【資料規模與約定】
對於10%的資料, 1<=n<=10;
對於30%的資料, 1<=n<=1000;
對於50%的資料, 1<=n<=10000;
對於100%的資料,1<=n<=100000,0<=Hi<=1000000。
(有點難理解~~~~,之後理解後在做!!!!)