SAS EM（一）關聯分析

關聯規則挖掘技術可以發現不同商品在消費者購買過程中的相關性。給定一組事務集合,其中每個事務是一個專案集;一個關聯規則是形如 X ->Y 的蘊涵式, X 和 Y 表示專案集,且 X∩ Y = Φ, X 和 Y 分別稱為關聯規則 X-> Y 的前提和結論。規則 X->Y 的支援度(Support) 是事務集中包含 X 和 Y 的事務數與所有事務數之比,記為 support(X->Y) ;規則 X->Y 的置信度(Confidence) 是指包含 X 和 Y 的事務數與包含 X 的事務數之比, 記為 confidence ( X->Y) 。

支援度用於衡量所發現規則的統計重要性,而置信度用於衡量關聯規則的可信程度。

一般來說,只有支援度和置信度均高的關聯規則才可能是消費者感興趣的、有用的規則。

 

以下例子參考https://blog.csdn.net/qq_36523839/article/details/82191677

（為了講解關聯分析中的支援度和置信度）

 

支援度：一個項集的支援度被定義為資料集中包含該項集的記錄所佔的比例，上圖中，豆奶的支援度為4/5，（豆奶、尿布）為3/5。支援度是針對項集來說的，因此可以定義一個最小支援度，只保留大於最小支援度的項集。

可信度（置信度）：針對如{尿布}->{葡萄酒}這樣的關聯規則來定義的。計算為 支援度{尿布，葡萄酒}/支援度{尿布}，其中{尿布，葡萄酒}的支援度為3/5，{尿布}的支援度為4/5，所以「尿布->葡萄酒」的可行度為3/4=0.75，這意味著尿布的記錄中，我們的規則有75%都適用。

 

Apriori  演演算法

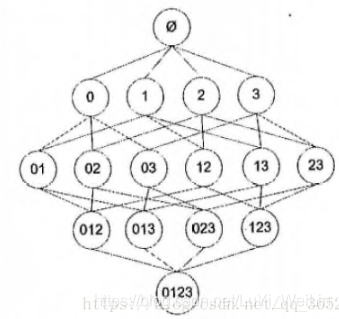
對於上圖，要計算 0,3 的支援度，直接的想法是遍歷每條記錄，統計包含有 0 和 3 的記錄的數量，使用該數量除以總記錄數，就可以得到支援度。而這只是針對單個集合 0,3. 要獲得每種可能集合的支援度就需要多次重複上述過程。對於上圖，雖然僅有4中物品，也需要遍歷資料15次。隨著物品數目的增加，遍歷次數會急劇增加，對於包含 N 種物品的資料集共有 2^N−1 種項集組合。為了降低計算時間，研究人員發現了 Apriori 原理，可以幫我們減少感興趣的頻繁項集的數目。

Apriori 的原理：如果某個項集是頻繁項集，那麼它所有的子集也是頻繁的。即如果 {0,1} 是頻繁的，那麼 {0}, {1} 也一定是頻繁的。

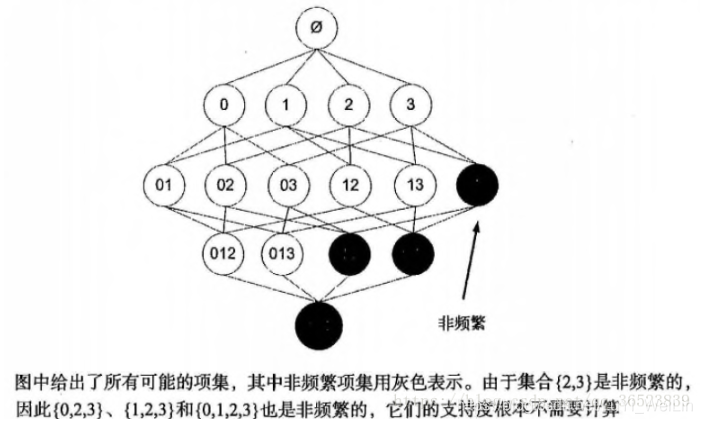
這個原理直觀上沒有什麼用，但是反過來看就有用了，也就是說如果一個項集是非頻繁的，那麼它的所有超集也是非頻繁的。

 

 

SAS EM實踐

建立資料來源（找到sas自帶資料集sampsio--assocs）

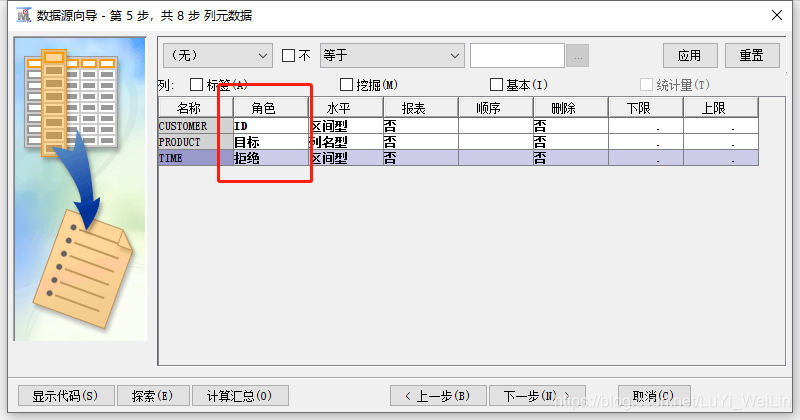
修改變數角色

 

建立流程圖

SAS內建有相關資料 ，把圖示拖下來

點解輸入節點修改資料來源

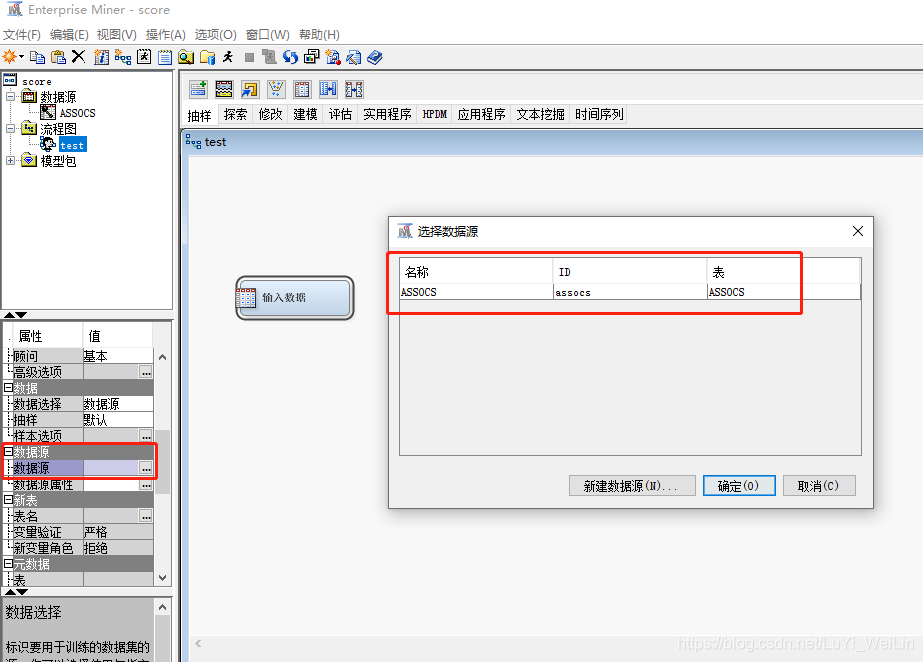
資料角色修改為事務

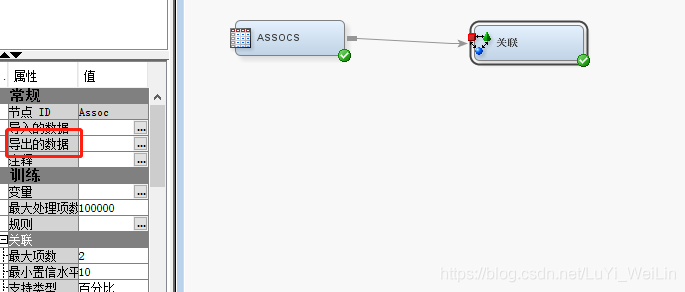
拖這個下來

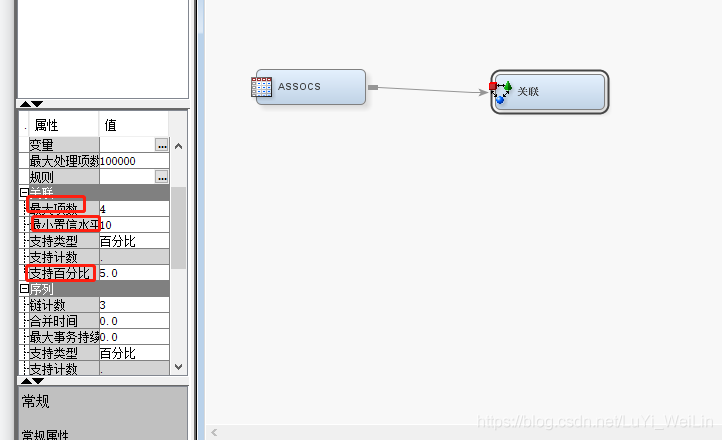
主要調節這三個（最小支援度，專案的最大數目和最小置信度），執行

檢視結果

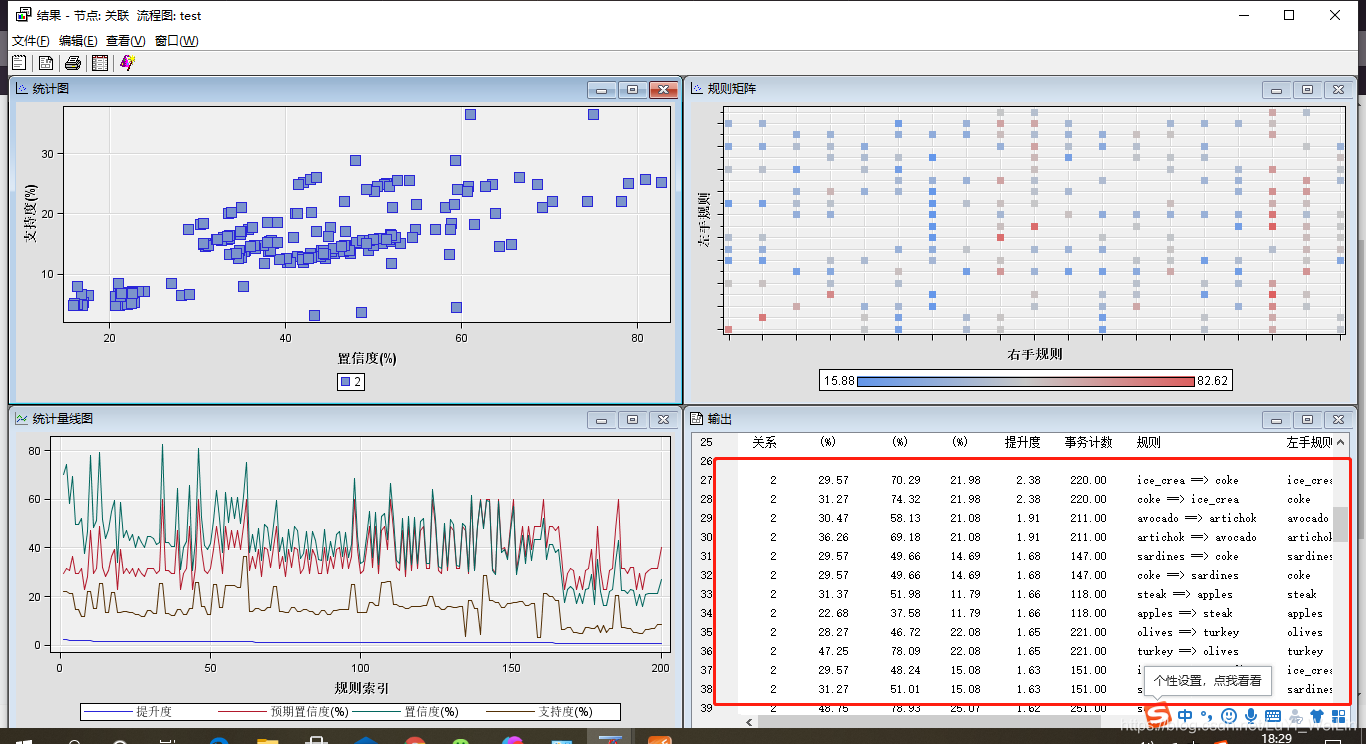
想要檢視全部結果可以

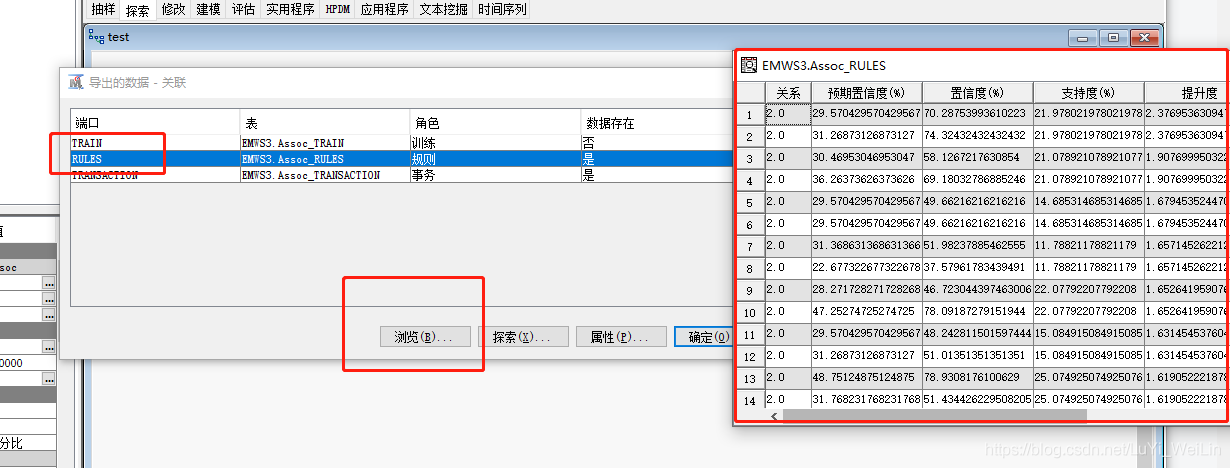
想要兩條以上的話

 

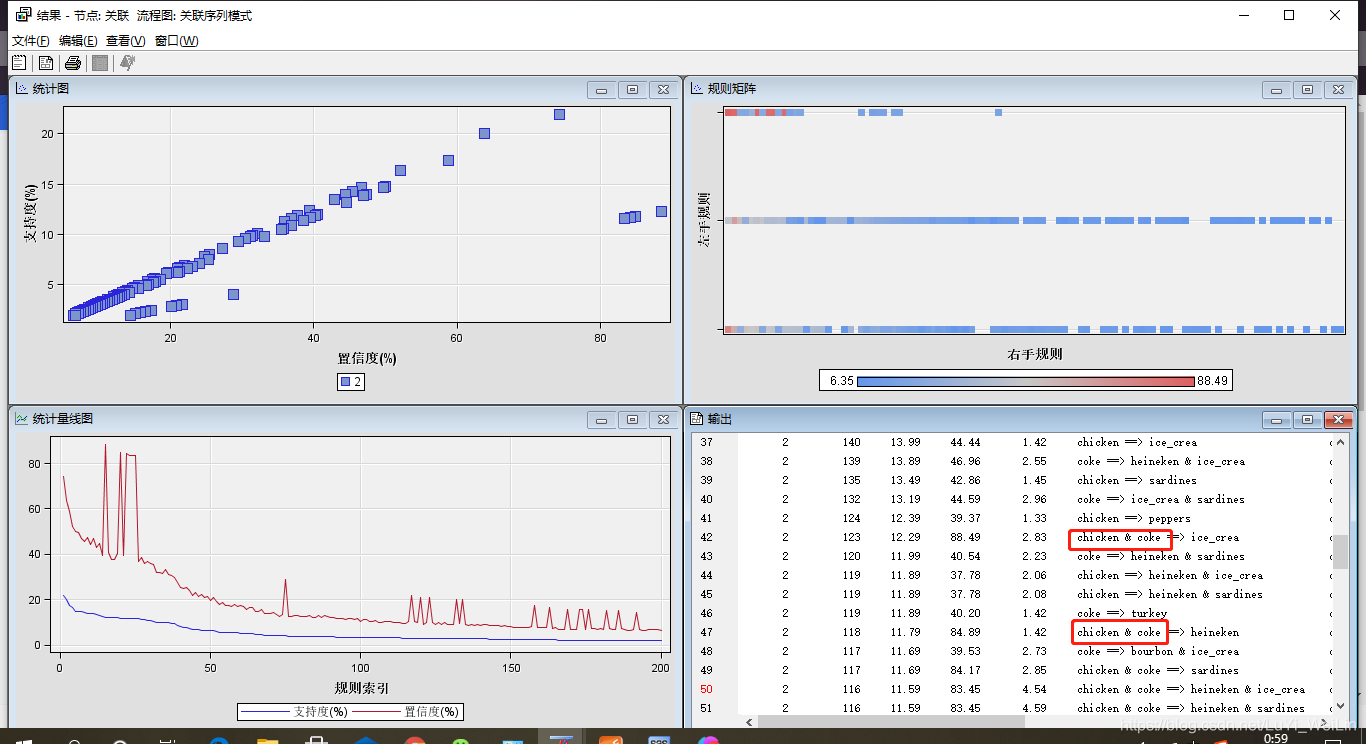
客製化型關聯分析實戰

在 SAS EM 中計算一個項與其他項之間的關聯規則。

1 建立一個新的資料集或者修改原資料集使它至少包含以下三個變數：
一個唯一的 ID 標識，一個目標變數，一個人工變數（如果值為 coke，則設定為 1 否則設定為 2）。

設定為1的話為X，即得出X-》Y的結論，想退出X的只需把下面的1和2順序互換

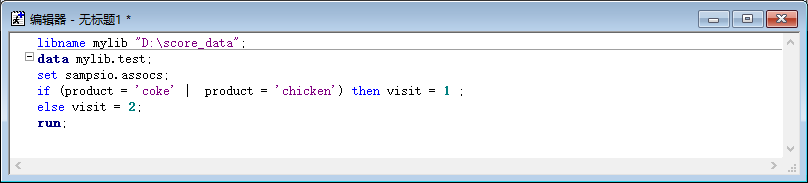
libname mylib "D:\score_data";
data mylib.test;
set sampsio.assocs;
if product = 'coke' then visit = 1 ;
else visit = 2;
run;

同理在sas em中匯入資料，穿建流程圖

操作同理（我們就會得出全為roke的）

 

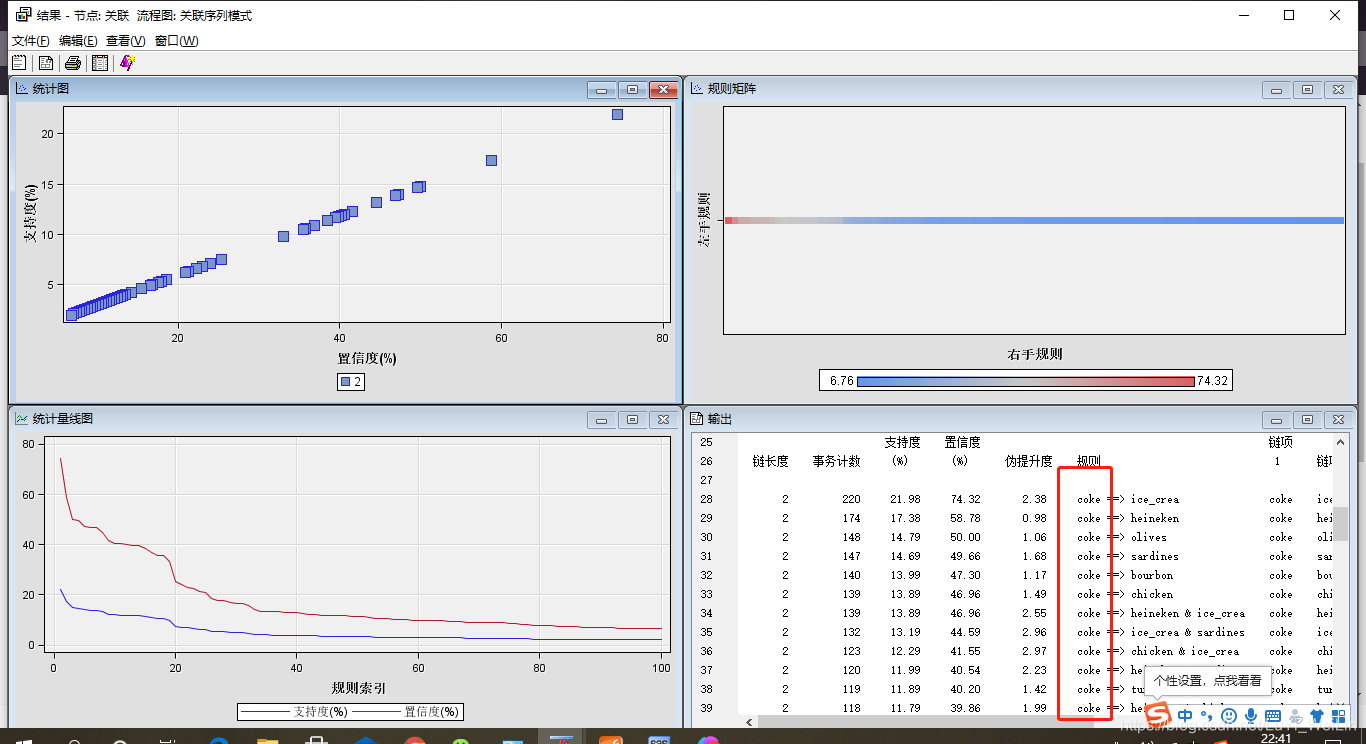
判斷關聯關係

參考自 https://blog.csdn.net/kl28978113/article/details/76304102

提升度

舉例子：

10000 個超市訂單（10000 個事務），其中購買三元牛奶（A事務）的 6000 個，購買伊利牛奶（B事務）的 7500 個，4000 個同時包含兩者。

三元牛奶（A事務）和伊利牛奶（B事務）的支援度為：P（A & B）= 4000 / 10000 = 0.4.

三元牛奶（A事務）對伊利牛奶（B事務）的置信度為：包含 A 的事務中同時包含 B 的佔包含 A 的事務比例。4000 / 6000 = 0.67，說明在購買三元牛奶後，有 0.67 的使用者去購買伊利牛奶。

伊利牛奶（B事務）對三元牛奶（A事務）的置信度為：包含 B 的事務中同時包含 A 的佔包含 B 的事務比例。4000 / 7500 = 0.53，說明在購買三元牛奶後，有 0.53 的使用者去購買伊利牛奶。

因為在沒有任何條件下，B事務的出現的比例是 0.75，而出現 A事務，且同時出現 B事務的比例是 0.67，也就是說設定了 A事務出現這個條件，B事務出現的比例反而降低了。這說明 A事務和 B事務是排斥的。

下面就有了提升度的概念。

我們把 0.67 / 0.75 的比值作為提升度，即 P（B | A） / P(B)，稱之為 A 條件對 B事務的提升度，即有 A 作為前提，對 B 出現的概率有什麼樣的影響，如果提升度 = 1 說明 A 和 B 沒有任何關聯，如果 < 1，說明 A事務和 B事務是排斥的，> 1，我們認為 A 和 B 是有關聯的，但是在具體的應用之中，我們認為提升度 > 3 才算作值得認可的關聯。

 

KULC 度量 + 不平衡比（IR）

提升度是一種很簡單的判斷關聯關係的手段，但是在實際應用過程中受零事務的影響比較大，零事務在上面例子中可以理解為既沒有購買三元牛奶也沒有購買伊利牛奶的訂單。數值為 10000 - 4000 - 2000 - 3500 = 500，可見在本例中，零事務非常小，但是在現實情況中，零事務是很大的。在本例中如果保持其他資料不變，把 10000 個事務改成 1000000 個事務，那麼計算出的提升度就會明顯增大，此時的零事務很大（1000000 - 4000 - 2000 - 3500），可見提升度是與零事務有關的。

KULC = 0.5 * P（B | A）+ 0.5 * P（A | B）

該公式表示 將兩種事件作為條件的置信度的均值,避開了支援度的計算,因此不會受零和事務的影響。在上例中，KULC 值 = ( 4000 / 6000 + 4000 / 7500 ) / 2 = 0.6

IR = P（B | A）/ P（A | B） ，IR 用來指示一種情況

假如在上例中 6000 個事務包含三元牛奶, 75000 個包含伊利牛奶,同時購買依舊為 4000

則：

KULC = 0.5 *（4000 / 75000 + 4000 / 6000）= 0.36

IR = 4000 / 6000 /（4000 / 75000）= 12.5

這說明這兩個事務的關聯關係非常不平衡，購買三元牛奶的顧客很可能同時會買伊利牛奶，而購買了伊利牛奶的使用者不太會再去買三元牛奶。很好理解，A 對 B 的支援度遠遠高於 B 對 A 的支援度。