機器學習模型評估指標總結！

↑↑↑關注後"星標"Datawhale

每日干貨 & 每月組隊學習，不錯過

 Datawhale乾貨 

作者：太子長琴，Datawhale優秀學習者

本文對機器學習模型評估指標進行了完整總結。機器學習的資料集一般被劃分為訓練集和測試集，訓練集用於訓練模型，測試集則用於評估模型。針對不同的機器學習問題（分類、排序、迴歸、序列預測等），評估指標決定了我們如何衡量模型的好壞。

一、Accuracy

準確率是最簡單的評價指標，公式如下：

但是存在明顯的缺陷：

• 當樣本分佈不均勻時，指標的結果由佔比大的類別決定。比如正樣本佔 99%，只要分類器將所有樣本都預測為正樣本就能獲得 99% 的準確率。

• 結果太籠統，實際應用中，我們可能更加關注某一類別樣本的情況。比如搜尋時會關心 「檢索出的資訊有多少是使用者感興趣的」，「使用者感興趣的資訊有多少被檢測出來了」 等等。

相應地還有錯誤率：分類錯誤的樣本佔總樣本的比例。

from sklearn.metrics import accuracy_score

y_pred = [0, 0, 1, 1]
y_true = [1, 0, 1, 0]
accuracy_score(y_true, y_pred) # 0.5

二、Precision Recall 和 F1

精準率（Precision）也叫查準率，衡量的是所有預測為正例的結果中，預測正確的（為真正例）比例。

召回率（Recall）也叫查全率，衡量的是實際的正例有多少被模型預測為正例。

在排序問題中，一般以 TopN 的結果作為正例，然後計算前 N 個位置上的精準率 Precision@N 和召回率 Recall@N。

精確率和召回率是一對相互矛盾的指標，一般來說高精準往往低召回，相反亦然。其實這個是比較直觀的，比如我們想要一個模型準確率達到 100%，那就意味著要保證每一個結果都是真正例，這就會導致有些正例被放棄；相反，要保證模型能將所有正例都預測為正例，意味著有些反例也會混進來。這背後的根本原因就在於我們的資料往往是隨機、且充滿噪聲的，並不是非黑即白。

精準率和召回率與混淆矩陣密切相關，混淆矩陣是將分類（二分類）結果通過矩陣的形式直觀展現出來：

真實情況	預測結果正例	預測結果反例
正例	TP(真正例)	FN(假反例)
反例	FP(假正例)	TN(真反例)

然後，很容易就得到精準率（P）和召回率（R）的計算公式：

得到 P 和 R 後就可以畫出更加直觀的P-R 圖（P-R 曲線），橫座標為召回率，縱座標是精準率。繪製方法如下：

• 對模型的學習結果進行排序（一般都有一個概率值）

• 按照上面的順序逐個把樣本作為正例進行預測，每次都可以得到一個 P R 值

• 將得到的 P R 值按照 R 為橫座標，P 為縱座標繪製曲線圖。

from typing import List, Tuple
import matplotlib.pyplot as plt

def get_confusion_matrix(
    y_pred: List[int], 
    y_true: List[int]
    ) -> Tuple[int, int, int, int]:
    
    length = len(y_pred)
    assert length == len(y_true)
    tp, fp, fn, tn = 0, 0, 0, 0
    for i in range(length):
        if y_pred[i] == y_true[i] and y_pred[i] == 1:
            tp += 1
        elif y_pred[i] == y_true[i] and y_pred[i] == 0:
            tn += 1
        elif y_pred[i] == 1 and y_true[i] == 0:
            fp += 1
        elif y_pred[i] == 0 and y_true[i] == 1:
            fn += 1
    return (tp, fp, tn, fn)
def calc_p(tp: int, fp: int) -> float:
    return tp / (tp + fp)
def calc_r(tp: int, fn: int) -> float:
    return tp / (tp + fn)
def get_pr_pairs(
    y_pred_prob: List[float], 
    y_true: List[int]
	) -> Tuple[List[int], List[int]]:
    ps = [1]
    rs = [0]
    for prob1 in y_pred_prob:
        y_pred_i = []
        for prob2 in y_pred_prob:
            if prob2 < prob1:
                y_pred_i.append(0)
            else:
                y_pred_i.append(1)
        tp, fp, tn, fn = get_confusion_matrix(y_pred_i, y_true)
        p = calc_p(tp, fp)
        r = calc_r(tp, fn)
        ps.append(p)
        rs.append(r)
    ps.append(0)
    rs.append(1)
    return ps, rs

y_pred_prob = [0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.52, 0.51, 0.505,
               0.4, 0.39, 0.38, 0.37, 0.36, 0.35, 0.34, 0.33, 0.3, 0.1]
y_true = [1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
y_pred = [1] * 10 + [0] * 10
ps, rs = get_pr_pairs(y_pred_prob, y_true)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 5))
ax.plot(rs, ps);

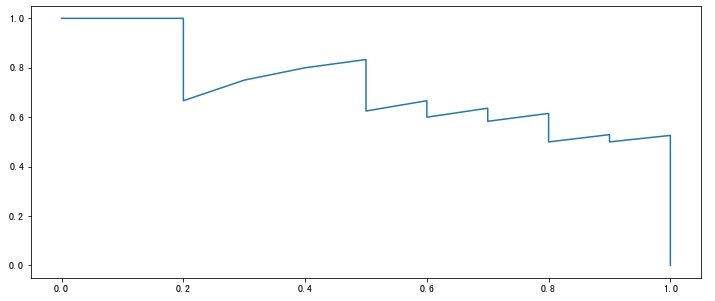
如果有多個模型就可以繪製多條 P-R 曲線：

• 如果某個模型的曲線完全被另外一個模型 「包住」（即後者更加凹向原點），那麼後者的效能一定優於前者。

• 如果多個模型的曲線發生交叉，此時不好判斷哪個模型較優，一個較為合理的方法是計算曲線下面積，但這個值不太好估算。

為了獲得模型優劣，需要綜合 P 和 R，平衡點 BEP（Break-Even Point）就是這樣一個度量，它是 P=R 時的取值，BPE 越遠離原點，說明模型效果越好。由於 BPE 過於簡單，實際中常用 F1 值衡量：

F1 有更一般的形式：

• 當 β > 1 時，更偏好召回

• 當 β < 1 時，更偏好精準

• 當 β = 1 時，平衡精準和召回，即為 F1

F1 其實來自精準和召回的加權調和平均：

當有多個混淆矩陣（多次訓練、多個資料集、多分類任務）時，有兩種方式估算 「全域性」 效能：

• macro 方法：先計算每個 PR，取平均後，再計算 F1

• micro 方法：先計算混淆矩陣元素的平均，再計算 PR 和 F1

三、RMSE

均方根誤差 RMSE（Root Mearn Square Error）主要用在迴歸模型，也就是俗稱的 R 方。計算公式為：

但是如果有非常嚴重的離群點時，那些點會影響 RMSE 的結果，針對這個問題：

• 如果離群點為噪聲，則去除這些點

• 如果離群點為正常樣本，可以重新建模

• 換一個評估指標，比如平均絕對百分比誤差 MAPE（Mean Absolute Percent Error），MAPE 對每個誤差進行了歸一化，一定程度上降低了離群點的影響。

四、ROC 和 AUC

受試者工作特徵 ROC（Receiver Operating Characteristic）曲線是另一個重要的二分類指標。它的橫座標是 「假正例率」 FPR（False Positive Rate），縱座標是 「真正例率」 TPR（True Positive Rate），計算公式如下：

繪製方法和上面的 P-R 曲線類似，不再贅述。

def calc_fpr(fp: int, tn: int) -> float:
    return fp / (fp + tn)
def calc_tpr(tp: int, fn: int) -> float:
    return tp / (tp + fn)
def get_ftpr_pairs(
    y_pred_prob: List[float], 
    y_true: List[int]
	) -> Tuple[List[int], List[int]]:
    fprs = [0]
    tprs = [0]
    for prob1 in y_pred_prob:
        y_pred_i = []
        for prob2 in y_pred_prob:
            if prob2 < prob1:
                y_pred_i.append(0)
            else:
                y_pred_i.append(1)
        tp, fp, tn, fn = get_confusion_matrix(y_pred_i, y_true)
        fpr = calc_fpr(fp, tn)
        tpr = calc_tpr(tp, fn)
        fprs.append(fpr)
        tprs.append(tpr)
    fprs.append(1)
    tprs.append(1)
    return fprs, tprs
fprs, tprs = get_ftpr_pairs(y_pred_prob, y_true)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 5))
ax.plot(fprs, tprs);

除此之外，還有一種繪製 ROC 曲線的方法：

• 假設有 m+ 個正例，m- 個負例，對模型輸出的預測概率按從高到低排序

• 然後依次將每個樣本的預測值作為閾值（即將該樣本作為正例），假設前一個座標為（x, y），若當前為真正例，對應標記點為（x, y+1/m+），若當前為假正例，則對應標記點為（x+1/m-, y）

• 將所有點相連即可得到 ROC 曲線

該方法和這種做法是一樣的：將縱座標的刻度間隔設為 1/m+，橫座標的刻度間隔設為 1/m-，從（0,0）開始，每遇到一個真正例就沿著縱軸繪製一個刻度間隔的曲線，假正例就沿著橫軸繪製一個刻度間隔的曲線，最終就可以得到 ROC 曲線。

def get_ftpr_pairs2(
    y_pred_prob: List[float], 
    y_true: List[int]
    ) -> Tuple[List[int], List[int]]:
    mplus = sum(y_true)
    msub = len(y_true) - mplus
    pairs = [(0, 0)]
    prev = (0, 0)
    length = len(y_pred_prob)
    assert length == len(y_true)
    for i in range(length):
        if y_true[i] == 1:
            pair = (prev[0], prev[1] + 1/mplus)
        else:
            pair = (prev[0] + 1/msub, prev[1])
        pairs.append(pair)
        prev = pair
    pairs.append((1, 1))
    fprs, tprs = [], []
    for pair in pairs:
        fprs.append(pair[0])
        tprs.append(pair[1])
    return fprs, tprs
fprs, tprs = get_ftpr_pairs2(y_pred_prob, y_true)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 5))
ax.plot(fprs, tprs);

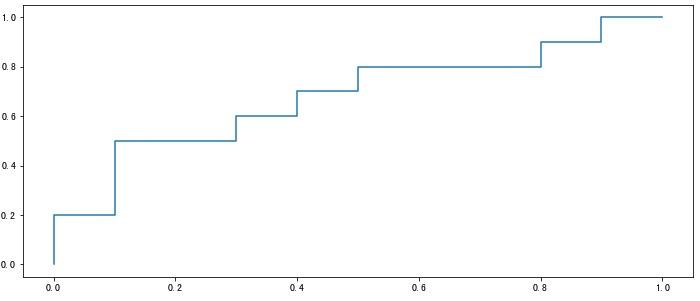
該方法和上面第一種方法得到的曲線完全一致。

多個模型時，與 P-R 曲線也是類似，如果某個模型的曲線完全 「包住」 另一個，則前者效能好於後者。如果曲線相互交叉，則比較曲線下面積：AUC（Area Under ROC Curve）。

AUC 取值一般在 0.5-1 之間，處於 y=x 直線的上方（如果不是的話，把預測概率翻轉成 1-p 就能獲得更好的模型）。AUC 值越大，說明模型越可能把真正例排在前面，效能越好。此時，假正例率很低同時真正例率很高，意味著召回高並且誤判率小。對角線對應著隨機模型（各佔 50%），（0，1）點對應的是理想模型，即所有正例 100% 召回且沒有一個負例被判別為正例。

AUC 面積可以通過以下公式進行估算：

AUC 考慮的是樣本預測的排序品質，與排序誤差緊密相連，排序 「損失」 loss 可定義為：

該式子的意思是，如果正例預測值小於負例，計 1 個罰分，如果相等則計 0.5 個罰分。顯然，該式對應的就是 ROC 曲線上面的面積。因此有：

與 P-R 曲線相比，ROC 曲線有一個特點：當正負樣本的分佈發生變化時，ROC 曲線形狀能基本保持不變，而 P-R 曲線的形狀一般會發生比較劇烈的變化。因此，當資料不均勻時，ROC 曲線更能夠反映模型好壞。而這背後的原因是：

• P-R 曲線關注的是真實的正例和預測的正例中（分別對應 Recall 和 Precision），實際是正例的比例

• ROC 曲線關注的是真實的正例和負例中（分別對應 TPR 和 FPR），被預測為正例的比例

五、KS

作為一個工程師，看到 KS 我們的第一反應應該是：既然已經有了 PR、ROC 等評價指標，為什麼還需要 KS？它解決了前面指標解決不了的什麼問題？它究竟有什麼特點？

KS Test（Kolmogorov-Smirnov）是由兩位蘇聯數學家 A.N. Kolmogorov 和 N.V. Smirnov 提出的，用於比較樣本與參考概率分佈或比較兩個樣本的非引數檢驗。

我們以兩樣本為例，假設 m 個 sample 來自分佈 F(x)，n 個來自 G(x)，定義 KS 統計量（KS 距離）為：

其中 F(x) 和 G(x) 都是經驗累積分佈函數 ECDF（empirical distribution function），定義如下：

sup 表示上確界，也是最小上界。

原始假設 H0：兩組 sample 來自統一分佈，在大樣本上，在置信水平 α 下如果滿足下面的條件則拒絕零假設（認為兩組樣本來自不同分佈）：

代入後得到：

常用的值如下：

from scipy import stats
rvs1 = stats.norm.rvs(size=200, loc=0., scale=1)
rvs2 = stats.norm.rvs(size=300, loc=0.5, scale=1.5)
stats.ks_2samp(rvs1, rvs2)
# 在置信度 0.05 水平下：1.358 * np.sqrt(500/60000) = 0.124
# Ks_2sampResult(statistic=0.265, pvalue=7.126401335710852e-08)
# 0.265 > 0.124 所以拒絕原假設，即認為兩組樣本來自不同分佈
# 事實上，即便是 0.005 的置信水平下依然要拒絕原假設
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 5))
ax.hist(rvs1, density=False, histtype='stepfilled', alpha=0.2, color='red');
ax.hist(rvs2, density=False, histtype='stepfilled', alpha=0.2, color='blue');

其中 statistic 就是 ks 統計量。

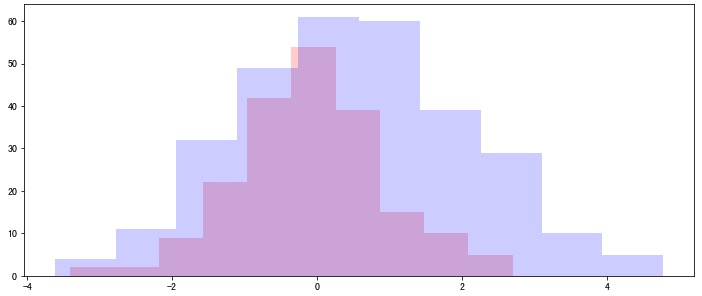
那這又和評價指標有啥關聯呢？

我們考慮這麼一種情況，假設資料集的 Label 並不是離散的（如二分類的 0-1），而是可能滿足一定分佈，也就是說標籤有很多灰色地帶。其實這在實際生活中倒是更加常見，以金融風控為例，不少特徵都是基於某個時間點做劃分的，比如逾期還款 x 天，這個 x 是非常靈活的，而且也很難說 x-1 天的就一定比 x+1 天的信用好。這就意味著給定特徵下，我們的標籤最好能夠有一定 「彈性」。

那麼，怎麼去體現這個 「彈性」 呢？因為 KS 正好是衡量兩個 「分佈」 的 「距離」，我們可以構造一個函數：

然後我們可以畫出 KS 曲線，可以證明，KS 和 ROC 等價，且滿足如下公式：

KS 的最大值就用來評估模型的區分度。而所謂的區分度正可以看作是正負例的差異，具體而言，如果正負例對於標籤沒有區分度，說明兩個樣本重疊較大；區分度越大，說明兩個概率分佈相隔越遠。回到 KS 上：

• 如果 KS 的最大值很小，說明 TPR 和 FPR 接近同一分佈，也就意味著真實的正例和負例被預測為正例的比例相似，說明模型很差。

• 如果 KS 的最大值很大，說明 TPR 和 FPR 區別很大，意味著真實的正例被預測為正例和真實的負例被預測為正例相差很大，說明模型效果較好（能夠區分真實正例和真實負例）。

事實上，KS 的確常用在金融風控中，用來評估模型的區分度，區分度越大說明模型的風險排序能力越強。但值太大也有問題（可能過擬合），一般超過 0.75 就認為過高，而低於 0.2 則過低。關於這個我們可以看圖說明：

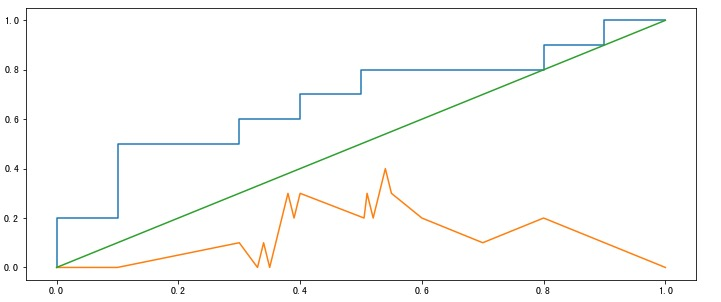
我們假設曲線光滑，那麼 AUC_KS ≈ 1/2 × max_KS，根據前面的公式：

由於上面提到的金融風控中 Label 的彈性，當 KS 過高時，ROC 的 AUC 就會很高，說明結果並沒有這種彈性（模糊性、連續性），此時模型有過擬合風險。

既然 KS 可以，那我們自然就要問了，t 檢驗行不行？因為 t 檢驗也是檢驗兩組樣本是否來自同一個分佈的統計量啊。答案是：不行。因為我們實際上是使用了它的定義（距離），而 t-test 的定義並沒有體現出這一點。

獨立雙樣本 t 檢驗，方差不相等：

獨立雙樣本 t 檢驗，樣本數相同，方差相似：

這裡的圖也可以說明這一點：

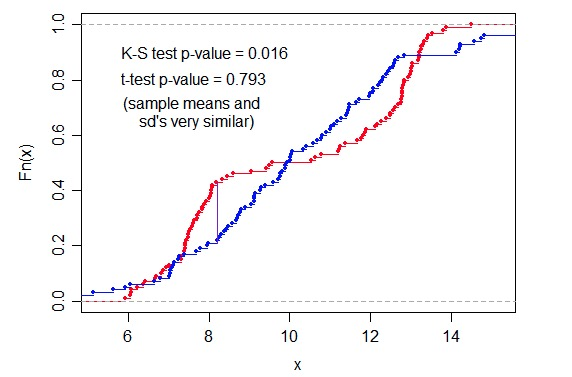
其他距離其實也沒有太多意義，因為 FPR 和 TPR 的 x 是一樣的，不同的也就是 y 值。

六、評分卡

評分卡模型是一個線性迴歸模型：

特徵覆蓋率高，保持穩定，特徵變數有明顯的可解釋性。樣本為 0 時可以根據專家歷史經驗設定權重；樣本為幾百時，可根據單特徵區分能力如 KS/IV 值等進行權重設定。

6.1 非線性處理

有兩種方式：WOE 處理和分桶。

證據權重 WOE（Weight of Evidence）是一種自變數編碼方案，定義為：

其中，Bi 表示第 i 個分組裡 bad label 的數量，Bt 為總的 bad label 數量；G 表示 good label。WOE 越大，bad label 比例越高，此時的 WOE 值可以作為該分組的特徵值。

分桶是指對有一定跳變的連續值特徵進行分桶，將弱線性特徵轉化為強線性特徵。

6.2 交叉特徵處理

主要採取對客戶分群的方式，對細分群體進行單獨建模（本質上是一種交叉特徵的體現）。

「整理不易，點贊三連↓