05.序列模型 W2.自然語言處理與詞嵌入(作業:詞向量+Emoji表情生成)
文章目錄
測試題:參考博文
作業1:
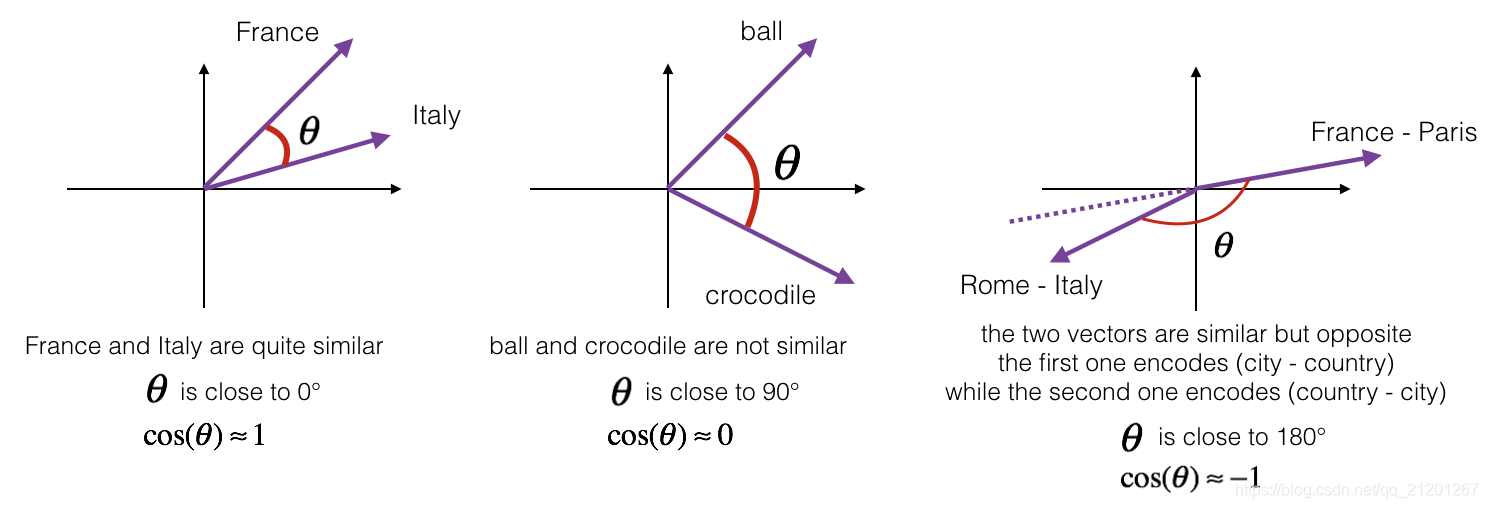
- 載入預訓練的 單詞向量,用 c o s ( θ ) cos(\theta) cos(θ) 餘弦夾角 測量相似度
- 使用詞嵌入解決類比問題
- 修改詞嵌入降低性比歧視
import numpy as np
from w2v_utils import *
這個作業使用 50-維的 GloVe vectors 表示單詞
words, word_to_vec_map = read_glove_vecs('data/glove.6B.50d.txt')
1. 餘弦相似度
CosineSimilarity(u, v) = u . v ∣ ∣ u ∣ ∣ 2 ∣ ∣ v ∣ ∣ 2 = c o s ( θ ) \text{CosineSimilarity(u, v)} = \frac {u . v} {||u||_2 ||v||_2} = cos(\theta) CosineSimilarity(u, v)=∣∣u∣∣2∣∣v∣∣2u.v=cos(θ)
其中 ∣ ∣ u ∣ ∣ 2 = ∑ i = 1 n u i 2 ||u||_2 = \sqrt{\sum_{i=1}^{n} u_i^2} ∣∣u∣∣2=∑i=1nui2
# GRADED FUNCTION: cosine_similarity
def cosine_similarity(u, v):
"""
Cosine similarity reflects the degree of similariy between u and v
Arguments:
u -- a word vector of shape (n,)
v -- a word vector of shape (n,)
Returns:
cosine_similarity -- the cosine similarity between u and v defined by the formula above.
"""
distance = 0.0
### START CODE HERE ###
# Compute the dot product between u and v (≈1 line)
dot = np.dot(u, v)
# Compute the L2 norm of u (≈1 line)
norm_u = np.linalg.norm(u)
# Compute the L2 norm of v (≈1 line)
norm_v = np.linalg.norm(v)
# Compute the cosine similarity defined by formula (1) (≈1 line)
cosine_similarity = dot/(norm_u*norm_v)
### END CODE HERE ###
return cosine_similarity
2. 單詞類比
例如:男人:女人 --> 國王:王后
# GRADED FUNCTION: complete_analogy
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
"""
Performs the word analogy task as explained above: a is to b as c is to ____.
Arguments:
word_a -- a word, string
word_b -- a word, string
word_c -- a word, string
word_to_vec_map -- dictionary that maps words to their corresponding vectors.
Returns:
best_word -- the word such that v_b - v_a is close to v_best_word - v_c, as measured by cosine similarity
"""
# convert words to lower case
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
### START CODE HERE ###
# Get the word embeddings v_a, v_b and v_c (≈1-3 lines)
e_a, e_b, e_c = word_to_vec_map[word_a],word_to_vec_map[word_b],word_to_vec_map[word_c]
### END CODE HERE ###
words = word_to_vec_map.keys()
max_cosine_sim = -100 # Initialize max_cosine_sim to a large negative number
best_word = None # Initialize best_word with None, it will help keep track of the word to output
# loop over the whole word vector set
for w in words:
# to avoid best_word being one of the input words, pass on them.
if w in [word_a, word_b, word_c] :
continue
### START CODE HERE ###
# Compute cosine similarity between the vector (e_b - e_a) and the vector ((w's vector representation) - e_c) (≈1 line)
cosine_sim = cosine_similarity(e_b-e_a, word_to_vec_map[w]-e_c)
# If the cosine_sim is more than the max_cosine_sim seen so far,
# then: set the new max_cosine_sim to the current cosine_sim and the best_word to the current word (≈3 lines)
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = w
### END CODE HERE ###
return best_word
測試:
triads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), ('man', 'woman', 'boy'), ('small', 'smaller', 'large')]
for triad in triads_to_try:
print ('{} -> {} :: {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))
輸出:
italy -> italian :: spain -> spanish
india -> delhi :: japan -> tokyo
man -> woman :: boy -> girl
small -> smaller :: large -> larger
額外測試:
good -> ok :: bad -> oops(糟糕)
father -> dad :: mother -> mom
3. 詞向量糾偏
研究反映在單詞嵌入中的性別偏見,並探索減少這種偏見的演演算法
g = word_to_vec_map['woman'] - word_to_vec_map['man']
print(g)
輸出:向量(50維)
[-0.087144 0.2182 -0.40986 -0.03922 -0.1032 0.94165
-0.06042 0.32988 0.46144 -0.35962 0.31102 -0.86824
0.96006 0.01073 0.24337 0.08193 -1.02722 -0.21122
0.695044 -0.00222 0.29106 0.5053 -0.099454 0.40445
0.30181 0.1355 -0.0606 -0.07131 -0.19245 -0.06115
-0.3204 0.07165 -0.13337 -0.25068714 -0.14293 -0.224957
-0.149 0.048882 0.12191 -0.27362 -0.165476 -0.20426
0.54376 -0.271425 -0.10245 -0.32108 0.2516 -0.33455
-0.04371 0.01258 ]
print ('List of names and their similarities with constructed vector:')
# girls and boys name
name_list = ['john', 'marie', 'sophie', 'ronaldo', 'priya', 'rahul', 'danielle', 'reza', 'katy', 'yasmin']
for w in name_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
輸出:
List of names and their similarities with constructed vector:
john -0.23163356145973724
marie 0.315597935396073
sophie 0.31868789859418784
ronaldo -0.31244796850329437
priya 0.17632041839009402
rahul -0.16915471039231716
danielle 0.24393299216283895
reza -0.07930429672199553
katy 0.2831068659572615
yasmin 0.2331385776792876
可以看出,
- 女性的名字往往與向量 𝑔 有正的餘弦相似性,
- 而男性的名字往往有負的餘弦相似性。結果似乎可以接受。
試試其他的詞語
print('Other words and their similarities:')
word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist',
'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer']
for w in word_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
輸出:
Other words and their similarities:
lipstick 0.2769191625638267
guns -0.1888485567898898
science -0.06082906540929701
arts 0.008189312385880337
literature 0.06472504433459932
warrior -0.20920164641125288
doctor 0.11895289410935041
tree -0.07089399175478091
receptionist 0.3307794175059374
technology -0.13193732447554302
fashion 0.03563894625772699
teacher 0.17920923431825664
engineer -0.0803928049452407
pilot 0.0010764498991916937
computer -0.10330358873850498
singer 0.1850051813649629
這些結果反映了某些性別歧視。例如,「computer 計算機」更接近「man 男人」,「literature 文學」更接近「woman 女人」。
下面看到如何使用Boliukbasi等人2016年提出的演演算法來減少這些向量的偏差。
請注意,有些詞對,如「演員」/「女演員」或「祖母」/「祖父」應保持性別特異性,而其他詞如「接待員」或「技術」應保持中立,即與性別無關。糾偏時,你必須區別對待這兩種型別的單詞
3.1 消除對非性別詞語的偏見
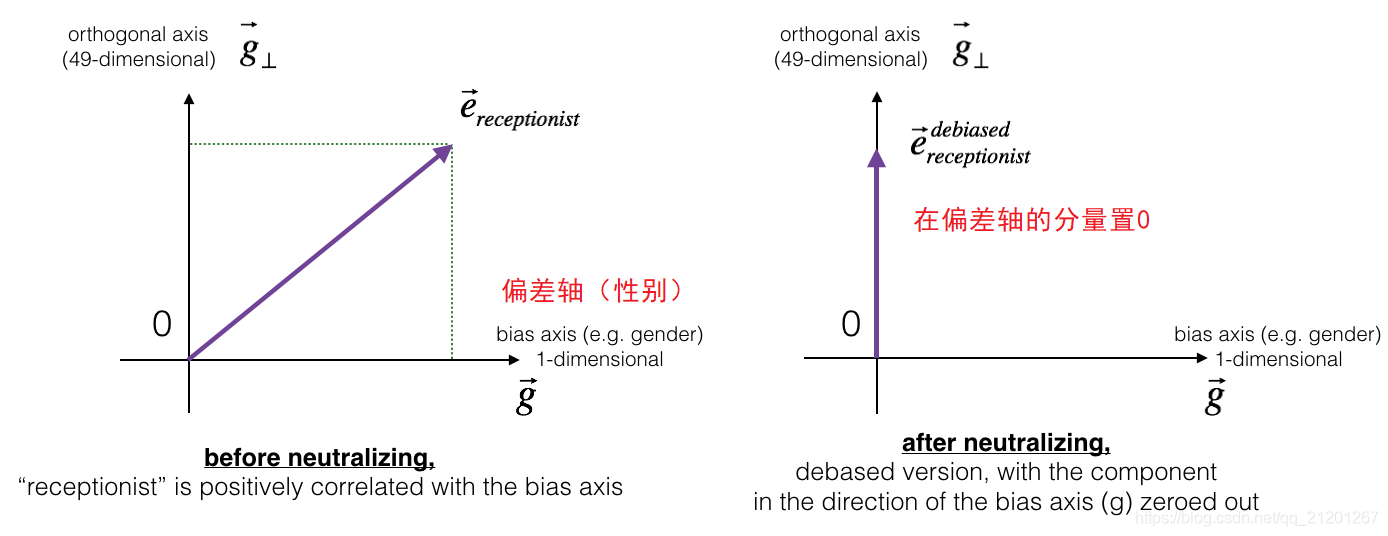
e b i a s _ c o m p o n e n t = e ⋅ g ∣ ∣ g ∣ ∣ 2 2 ∗ g e^{bias\_component} = \frac{e \cdot g}{||g||_2^2} * g ebias_component=∣∣g∣∣22e⋅g∗g
e d e b i a s e d = e − e b i a s _ c o m p o n e n t e^{debiased} = e - e^{bias\_component} edebiased=e−ebias_component
def neutralize(word, g, word_to_vec_map):
"""
Removes the bias of "word" by projecting it on the space orthogonal to the bias axis.
This function ensures that gender neutral words are zero in the gender subspace.
Arguments:
word -- string indicating the word to debias
g -- numpy-array of shape (50,), corresponding to the bias axis (such as gender)
word_to_vec_map -- dictionary mapping words to their corresponding vectors.
Returns:
e_debiased -- neutralized word vector representation of the input "word"
"""
### START CODE HERE ###
# Select word vector representation of "word". Use word_to_vec_map. (≈ 1 line)
e = word_to_vec_map[word]
# Compute e_biascomponent using the formula give above. (≈ 1 line)
e_biascomponent = np.dot(e, g)/np.linalg.norm(g)**2*g
# Neutralize e by substracting e_biascomponent from it
# e_debiased should be equal to its orthogonal projection. (≈ 1 line)
e_debiased = e - e_biascomponent
### END CODE HERE ###
return e_debiased
測試:
e = "receptionist"
print("cosine similarity between " + e + " and g, before neutralizing: ", cosine_similarity(word_to_vec_map["receptionist"], g))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("cosine similarity between " + e + " and g, after neutralizing: ", cosine_similarity(e_debiased, g))
輸出:
cosine similarity between receptionist and g,
before neutralizing: 0.3307794175059374
cosine similarity between receptionist and g,
after neutralizing: -2.099120994400013e-17
糾偏以後,receptionist(接待員)與性別的相似度接近於 0,既不偏向男人,也不偏向女人
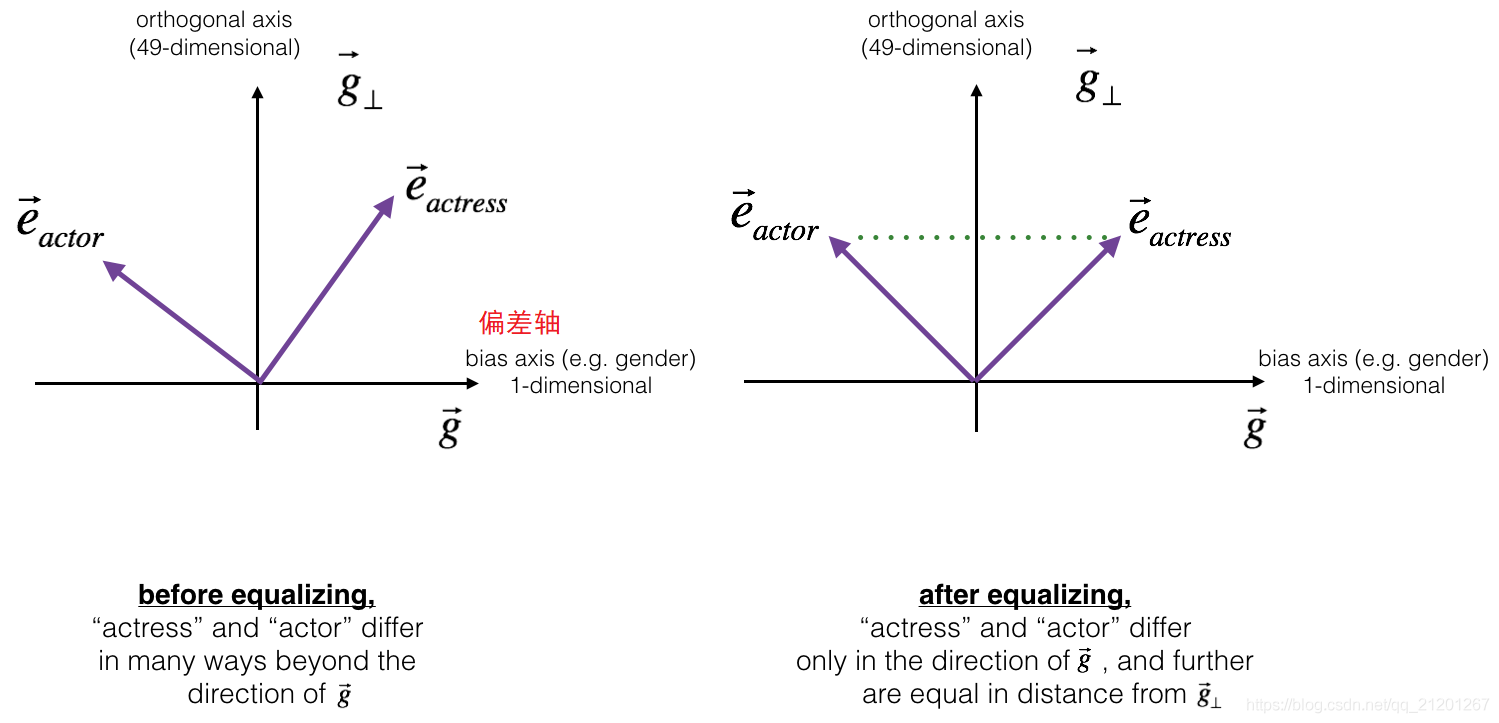
3.2 性別詞的均衡演演算法
如何將糾偏應用於單詞對,例如「女演員」和「演員」。
均衡化應用:只希望通過性別屬性而有所不同的單詞對。
作為一個具體的例子,假設「女演員」比「演員」更接近「保姆」,通過對「保姆」進行中性化,我們可以減少與保姆相關的性別刻板印象。但這仍然不能保證「演員」和「女演員」與「保姆」的距離相等,均衡演演算法可以處理這一點。
μ
=
e
w
1
+
e
w
2
2
\mu = \frac{e_{w1} + e_{w2}}{2}
μ=2ew1+ew2
μ B = μ ⋅ bias_axis ∣ ∣ bias_axis ∣ ∣ 2 2 ∗ bias_axis \mu_{B} = \frac {\mu \cdot \text{bias\_axis}}{||\text{bias\_axis}||_2^2} *\text{bias\_axis} μB=∣∣bias_axis∣∣22μ⋅bias_axis∗bias_axis
μ ⊥ = μ − μ B \mu_{\perp} = \mu - \mu_{B} μ⊥=μ−μB
e w 1 B = e w 1 ⋅ bias_axis ∣ ∣ bias_axis ∣ ∣ 2 2 ∗ bias_axis e_{w1B} = \frac {e_{w1} \cdot \text{bias\_axis}}{||\text{bias\_axis}||_2^2} *\text{bias\_axis} ew1B=∣∣bias_axis∣∣22ew1⋅bias_axis∗bias_axis
e w 2 B = e w 2 ⋅ bias_axis ∣ ∣ bias_axis ∣ ∣ 2 2 ∗ bias_axis e_{w2B} = \frac {e_{w2} \cdot \text{bias\_axis}}{||\text{bias\_axis}||_2^2} *\text{bias\_axis} ew2B=∣∣bias_axis∣∣22ew2⋅bias_axis∗bias_axis
e w 1 B c o r r e c t e d = ∣ 1 − ∣ ∣ μ ⊥ ∣ ∣ 2 2 ∣ ∗ e w1B − μ B ∣ ( e w 1 − μ ⊥ ) − μ B ) ∣ e_{w1B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w1B}} - \mu_B} {|(e_{w1} - \mu_{\perp}) - \mu_B)|} ew1Bcorrected=∣1−∣∣μ⊥∣∣22∣∗∣(ew1−μ⊥)−μB)∣ew1B−μB
e w 2 B c o r r e c t e d = ∣ 1 − ∣ ∣ μ ⊥ ∣ ∣ 2 2 ∣ ∗ e w2B − μ B ∣ ( e w 2 − μ ⊥ ) − μ B ) ∣ e_{w2B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w2B}} - \mu_B} {|(e_{w2} - \mu_{\perp}) - \mu_B)|} ew2Bcorrected=∣1−∣∣μ⊥∣∣22∣∗∣(ew2−μ⊥)−μB)∣ew2B−μB
e 1 = e w 1 B c o r r e c t e d + μ ⊥ e_1 = e_{w1B}^{corrected} + \mu_{\perp} e1=ew1Bcorrected+μ⊥
e 2 = e w 2 B c o r r e c t e d + μ ⊥ e_2 = e_{w2B}^{corrected} + \mu_{\perp} e2=ew2Bcorrected+μ⊥
def equalize(pair, bias_axis, word_to_vec_map):
"""
Debias gender specific words by following the equalize method described in the figure above.
Arguments:
pair -- pair of strings of gender specific words to debias, e.g. ("actress", "actor")
bias_axis -- numpy-array of shape (50,), vector corresponding to the bias axis, e.g. gender
word_to_vec_map -- dictionary mapping words to their corresponding vectors
Returns
e_1 -- word vector corresponding to the first word
e_2 -- word vector corresponding to the second word
"""
### START CODE HERE ###
# Step 1: Select word vector representation of "word". Use word_to_vec_map. (≈ 2 lines)
w1, w2 = pair[0], pair[1]
e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2]
# Step 2: Compute the mean of e_w1 and e_w2 (≈ 1 line)
mu = (e_w1+e_w2)/2
# Step 3: Compute the projections of mu over the bias axis and the orthogonal axis (≈ 2 lines)
mu_B = np.dot(mu, bias_axis)/np.linalg.norm(bias_axis)**2*bias_axis
mu_orth = mu-mu_B
# Step 4: Use equations (7) and (8) to compute e_w1B and e_w2B (≈2 lines)
e_w1B = np.dot(e_w1,bias_axis)/np.linalg.norm(bias_axis)**2*bias_axis
e_w2B = np.dot(e_w2,bias_axis)/np.linalg.norm(bias_axis)**2*bias_axis
# Step 5: Adjust the Bias part of e_w1B and e_w2B using the formulas (9) and (10) given above (≈2 lines)
corrected_e_w1B = np.sqrt(np.abs(1-np.linalg.norm(mu_orth)**2))*np.divide((e_w1B-mu_B),np.abs(e_w1-mu_orth-mu_B))
corrected_e_w2B = np.sqrt(np.abs(1-np.linalg.norm(mu_orth)**2))*np.divide((e_w2B-mu_B),np.abs(e_w2-mu_orth-mu_B))
# Step 6: Debias by equalizing e1 and e2 to the sum of their corrected projections (≈2 lines)
e1 = corrected_e_w1B+mu_orth
e2 = corrected_e_w2B+mu_orth
### END CODE HERE ###
return e1, e2
測試:
print("cosine similarities before equalizing:")
print("cosine_similarity(word_to_vec_map[\"man\"], gender) = ", cosine_similarity(word_to_vec_map["man"], g))
print("cosine_similarity(word_to_vec_map[\"woman\"], gender) = ", cosine_similarity(word_to_vec_map["woman"], g))
print()
e1, e2 = equalize(("man", "woman"), g, word_to_vec_map)
print("cosine similarities after equalizing:")
print("cosine_similarity(e1, gender) = ", cosine_similarity(e1, g))
print("cosine_similarity(e2, gender) = ", cosine_similarity(e2, g))
輸出:
cosine similarities before equalizing:
cosine_similarity(word_to_vec_map["man"], gender) = -0.11711095765336832
cosine_similarity(word_to_vec_map["woman"], gender) = 0.35666618846270376
cosine similarities after equalizing:
cosine_similarity(e1, gender) = -0.7165727525843935
cosine_similarity(e2, gender) = 0.7396596474928909
平衡以後,相似度符號相反,數值接近
作業2:Emojify表情生成
使用 word vector representations 建立 Emojifier
讓你的訊息更有表現力😁,使用單詞向量的話,可以是你的單詞沒有在該表情的關聯裡面,也能學習到可以使用該表情。
- 匯入一些包
import numpy as np
from emo_utils import *
import emoji
import matplotlib.pyplot as plt
%matplotlib inline
1. Baseline model: Emojifier-V1
1.1 資料集
X:127個句子(字串)
Y:整型 標籤 0 - 4 ,是相關的句子的表情
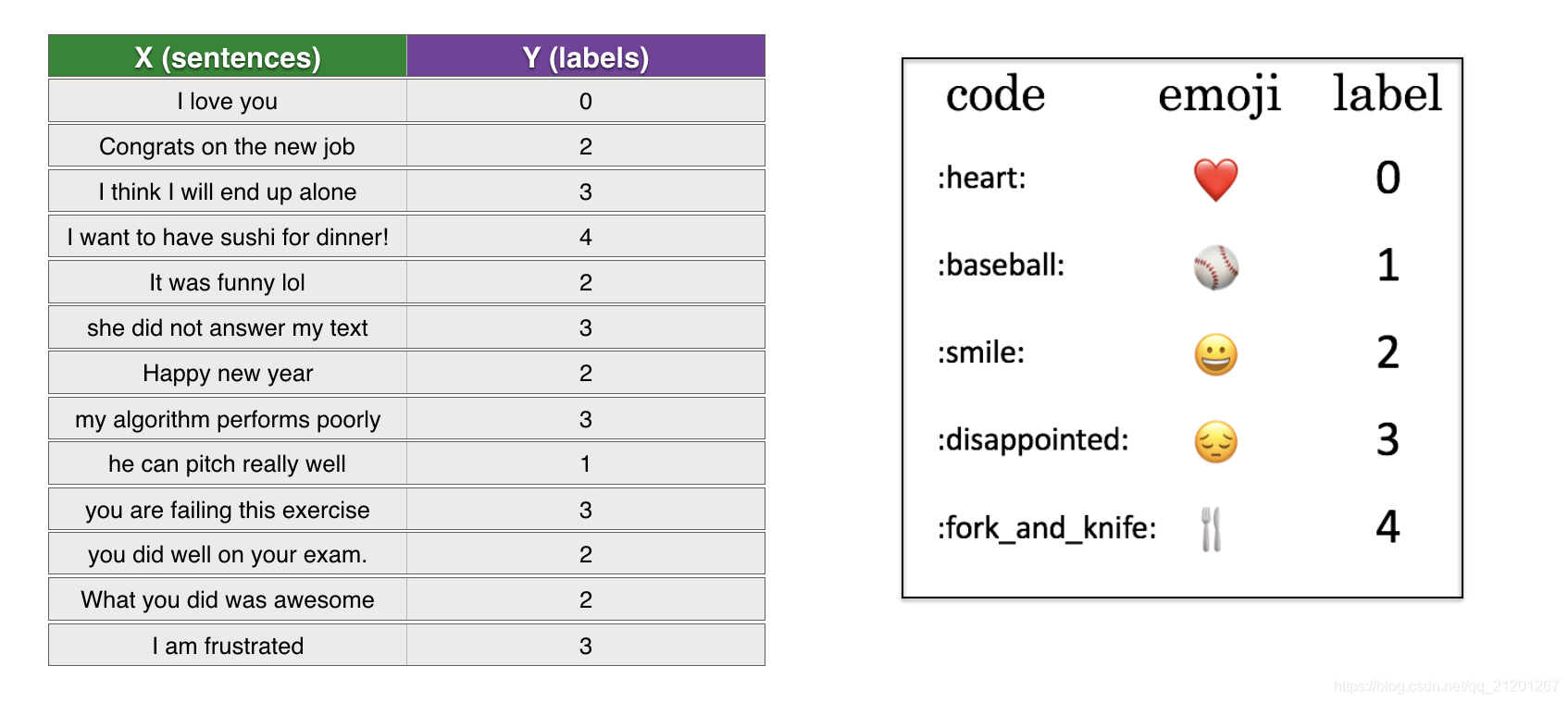
- 載入資料集,訓練集(127個樣本),測試集(56個樣本)
X_train, Y_train = read_csv('data/train_emoji.csv')
X_test, Y_test = read_csv('data/tesss.csv')
maxLen = len(max(X_train, key=len).split())
print(max(X_train, key=len).split())
輸出:
['I', 'am', 'so', 'impressed', 'by', 'your', 'dedication', 'to', 'this', 'project']
最長的句子是10個單詞
- 檢視資料集
index = 3
print(X_train[index], label_to_emoji(Y_train[index]))
輸出:
Miss you so much ❤️
1.2 模型預覽
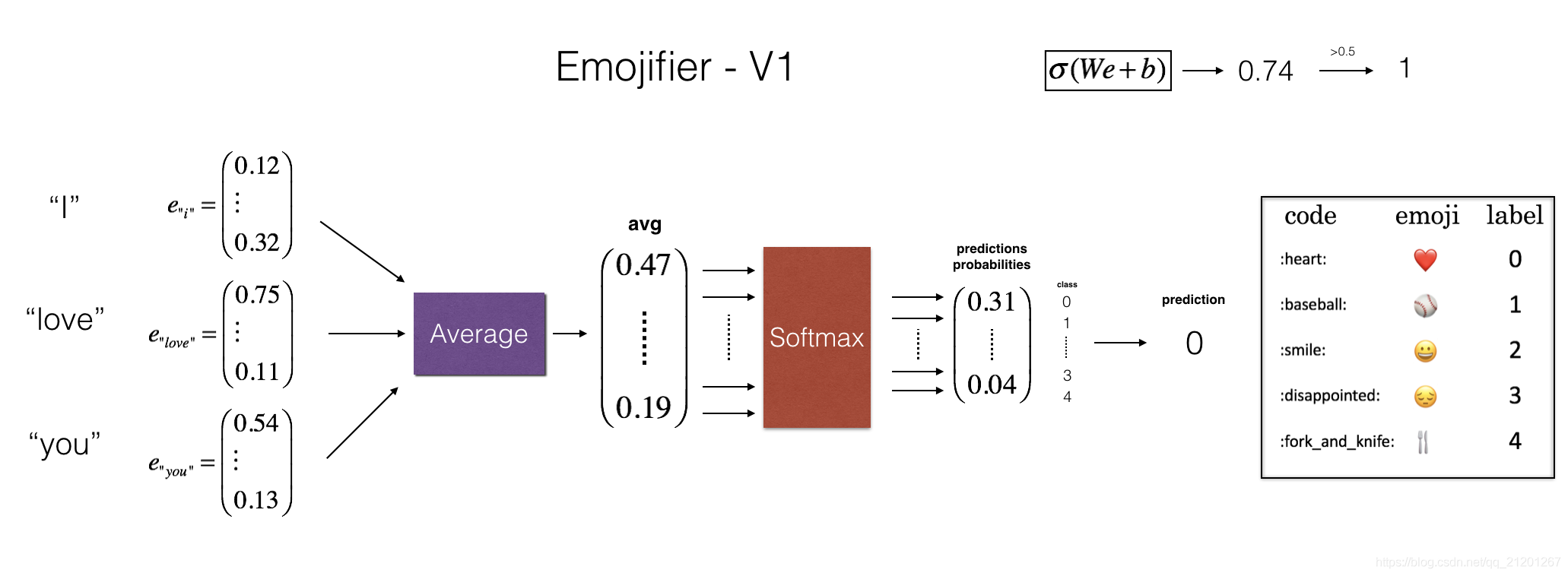
為了方便,把 Y 的形狀從
(
m
,
1
)
(m,1)
(m,1) 改成 one-hot 表示
(
m
,
5
)
(m,5)
(m,5)
Y_oh_train = convert_to_one_hot(Y_train, C = 5)
Y_oh_test = convert_to_one_hot(Y_test, C = 5)
index = 52
print(Y_train[index], "is converted into one hot", Y_oh_train[index])
輸出:
3 is converted into one hot [0. 0. 0. 1. 0.]
1.3 實現 Emojifier-V1
使用預訓練的 50-dimensional GloVe embeddings
word_to_index, index_to_word, word_to_vec_map = read_glove_vecs('data/glove.6B.50d.txt')
- 檢查下是否正確
word = "cucumber"
index = 289846
print("the index of", word, "in the vocabulary is", word_to_index[word])
print("the", str(index) + "th word in the vocabulary is", index_to_word[index])
輸出:
the index of cucumber in the vocabulary is 113317
the 289846th word in the vocabulary is potatos
實現 sentence_to_avg():
- 轉換每個句子為小寫,並切分成單詞
- 每個句子的單詞,使用 GloVe 向量表示,然後求句子的平均
# GRADED FUNCTION: sentence_to_avg
def sentence_to_avg(sentence, word_to_vec_map):
"""
Converts a sentence (string) into a list of words (strings). Extracts the GloVe representation of each word
and averages its value into a single vector encoding the meaning of the sentence.
Arguments:
sentence -- string, one training example from X
word_to_vec_map -- dictionary mapping every word in a vocabulary into its 50-dimensional vector representation
Returns:
avg -- average vector encoding information about the sentence, numpy-array of shape (50,)
"""
### START CODE HERE ###
# Step 1: Split sentence into list of lower case words (≈ 1 line)
words = sentence.lower().split()
# Initialize the average word vector, should have the same shape as your word vectors.
avg = np.zeros(word_to_vec_map[words[0]].shape)
# Step 2: average the word vectors. You can loop over the words in the list "words".
for w in words:
avg += word_to_vec_map[w]
avg /= len(words)
### END CODE HERE ###
return avg
測試:
avg = sentence_to_avg("Morrocan couscous is my favorite dish", word_to_vec_map)
print("avg = ", avg)
輸出:
avg = [-0.008005 0.56370833 -0.50427333 0.258865 0.55131103 0.03104983
-0.21013718 0.16893933 -0.09590267 0.141784 -0.15708967 0.18525867
0.6495785 0.38371117 0.21102167 0.11301667 0.02613967 0.26037767
0.05820667 -0.01578167 -0.12078833 -0.02471267 0.4128455 0.5152061
0.38756167 -0.898661 -0.535145 0.33501167 0.68806933 -0.2156265
1.797155 0.10476933 -0.36775333 0.750785 0.10282583 0.348925
-0.27262833 0.66768 -0.10706167 -0.283635 0.59580117 0.28747333
-0.3366635 0.23393817 0.34349183 0.178405 0.1166155 -0.076433
0.1445417 0.09808667]
模型
用sentence_to_avg() 處理完以後,進行前向傳播、計算損失、後向傳播更新引數
z ( i ) = W . a v g ( i ) + b z^{(i)} = W . avg^{(i)} + b z(i)=W.avg(i)+b
a ( i ) = s o f t m a x ( z ( i ) ) a^{(i)} = softmax(z^{(i)}) a(i)=softmax(z(i))
L ( i ) = − ∑ k = 0 n y − 1 Y o h k ( i ) ∗ l o g ( a k ( i ) ) \mathcal{L}^{(i)} = - \sum_{k = 0}^{n_y - 1} Yoh^{(i)}_k * log(a^{(i)}_k) L(i)=−k=0∑ny−1Yohk(i)∗log(ak(i))
# GRADED FUNCTION: model
def model(X, Y, word_to_vec_map, learning_rate = 0.01, num_iterations = 400):
"""
Model to train word vector representations in numpy.
Arguments:
X -- input data, numpy array of sentences as strings, of shape (m, 1)
Y -- labels, numpy array of integers between 0 and 7, numpy-array of shape (m, 1)
word_to_vec_map -- dictionary mapping every word in a vocabulary into its 50-dimensional vector representation
learning_rate -- learning_rate for the stochastic gradient descent algorithm
num_iterations -- number of iterations
Returns:
pred -- vector of predictions, numpy-array of shape (m, 1)
W -- weight matrix of the softmax layer, of shape (n_y, n_h)
b -- bias of the softmax layer, of shape (n_y,)
"""
np.random.seed(1)
# Define number of training examples
m = Y.shape[0] # number of training examples
n_y = 5 # number of classes
n_h = 50 # dimensions of the GloVe vectors
# Initialize parameters using Xavier initialization
W = np.random.randn(n_y, n_h) / np.sqrt(n_h)
b = np.zeros((n_y,))
# Convert Y to Y_onehot with n_y classes
Y_oh = convert_to_one_hot(Y, C = n_y)
# Optimization loop
for t in range(num_iterations): # Loop over the number of iterations
for i in range(m): # Loop over the training examples
### START CODE HERE ### (≈ 4 lines of code)
# Average the word vectors of the words from the i'th training example
avg = sentence_to_avg(X[i], word_to_vec_map)
# Forward propagate the avg through the softmax layer
z = np.dot(W, avg)+b
a = softmax(z)
# Compute cost using the i'th training label's one hot representation and "A" (the output of the softmax)
cost = - sum(Y_oh[i]*np.log(a))
### END CODE HERE ###
# Compute gradients
dz = a - Y_oh[i]
dW = np.dot(dz.reshape(n_y,1), avg.reshape(1, n_h))
db = dz
# Update parameters with Stochastic Gradient Descent
W = W - learning_rate * dW
b = b - learning_rate * db
if t % 100 == 0:
print("Epoch: " + str(t) + " --- cost = " + str(cost))
pred = predict(X, Y, W, b, word_to_vec_map)
return pred, W, b
1.4 在訓練集上測試
print("Training set:")
pred_train = predict(X_train, Y_train, W, b, word_to_vec_map)
print('Test set:')
pred_test = predict(X_test, Y_test, W, b, word_to_vec_map)
輸出:
Training set:
Accuracy: 0.9772727272727273
Test set:
Accuracy: 0.8571428571428571
隨機猜測的話,平均概率是 20%(1/5),模型的效果很不錯,在只有127個訓練樣本的情況下
讓我們來測試:
- 我們在訓練集裡看到了
I love you有標籤 ❤️ - 我們來檢查下使用
adore(愛慕)(該詞沒有在訓練集出現過)
X_my_sentences = np.array(["i adore you", "i love you", "funny lol", "lets play with a ball", "food is ready", "not feeling happy"])
Y_my_labels = np.array([[0], [0], [2], [1], [4],[3]])
pred = predict(X_my_sentences, Y_my_labels , W, b, word_to_vec_map)
print_predictions(X_my_sentences, pred)
輸出:
Accuracy: 0.8333333333333334(5/6,最後一個錯了)
i adore you ❤️(adore 跟 love 有相似的 embedding )
i love you ❤️
funny lol 😄
lets play with a ball ⚾
food is ready 🍴
not feeling happy 😄(識別錯誤,不能發現 not 這類組合詞)
檢查錯誤:
列印混淆矩陣可以幫助瞭解哪些樣本模型預測不準。
一個混淆矩陣顯示了一個標籤是一個類(真實標籤)的例子被演演算法用不同的類(預測錯誤)錯誤標記的頻率
print(Y_test.shape)
print(' '+ label_to_emoji(0)+ ' ' + label_to_emoji(1) + ' ' + label_to_emoji(2)+ ' ' + label_to_emoji(3)+' ' + label_to_emoji(4))
print(pd.crosstab(Y_test, pred_test.reshape(56,), rownames=['Actual'], colnames=['Predicted'], margins=True))
plot_confusion_matrix(Y_test, pred_test)


2. Emojifier-V2: Using LSTMs in Keras
讓我們構建一個LSTM模型,它將單詞序列作為輸入。這個模型將能夠考慮單詞順序。
Emojifier-V2 將繼續使用預先訓練過的 word embeddings 來表示單詞,將把它們輸入LSTM,LSTM的任務是預測最合適的表情符號。
- 匯入一些包
import numpy as np
np.random.seed(0)
from keras.models import Model
from keras.layers import Dense, Input, Dropout, LSTM, Activation
from keras.layers.embeddings import Embedding
from keras.preprocessing import sequence
from keras.initializers import glorot_uniform
np.random.seed(1)
2.1 模型預覽
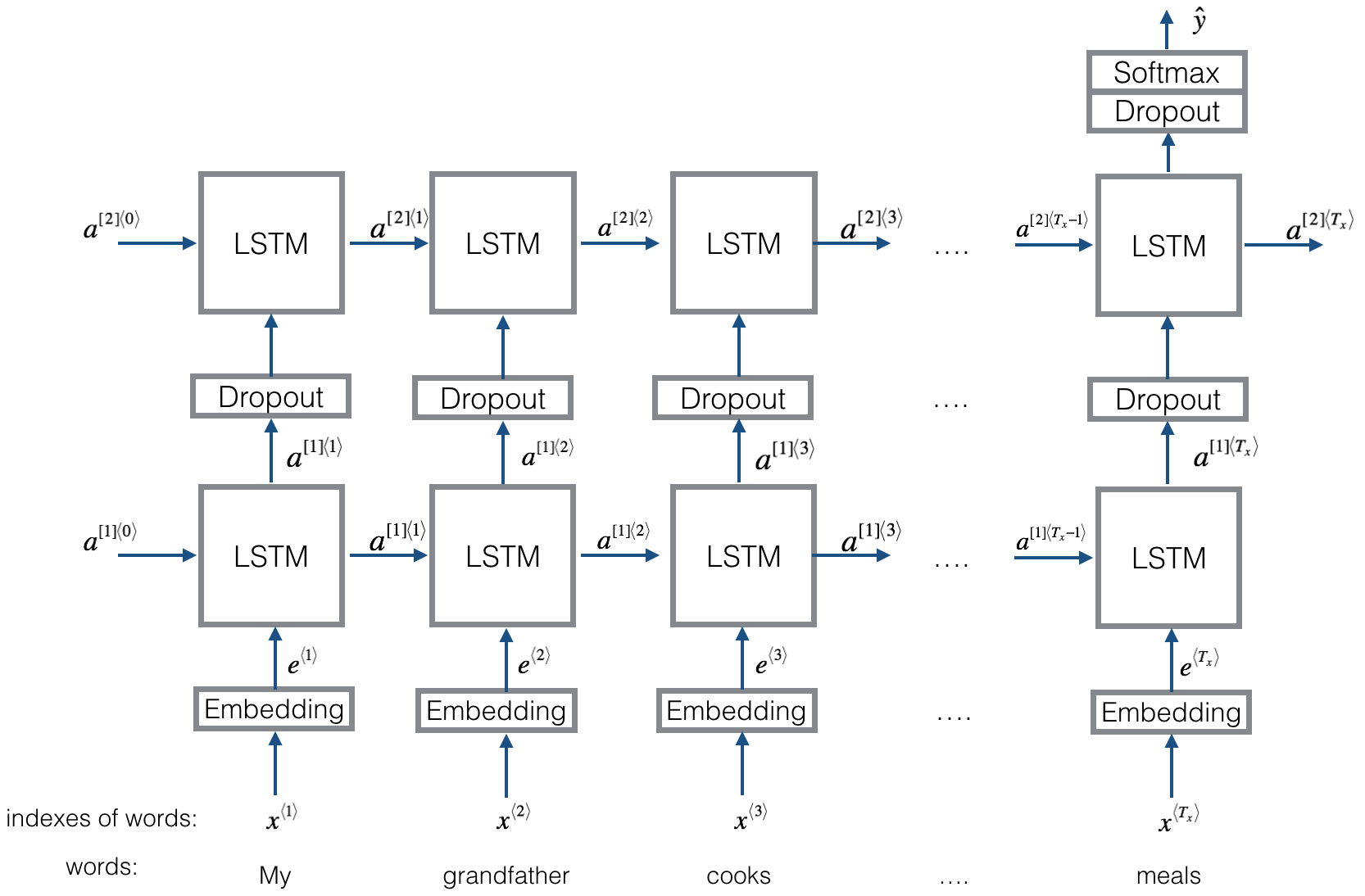
2.2 Keras and mini-batching
為了使樣本能夠批次訓練,我們必須處理句子,使他們的長度都一樣長,長度不夠最大長度的,後面補上一些 0 向量 ( e i , e l o v e , e y o u , 0 ⃗ , 0 ⃗ , … , 0 ⃗ ) (e_{i}, e_{love}, e_{you}, \vec{0}, \vec{0}, \ldots, \vec{0}) (ei,elove,eyou,0,0,…,0)
2.3 Embedding 層
https://keras.io/zh/layers/embeddings/
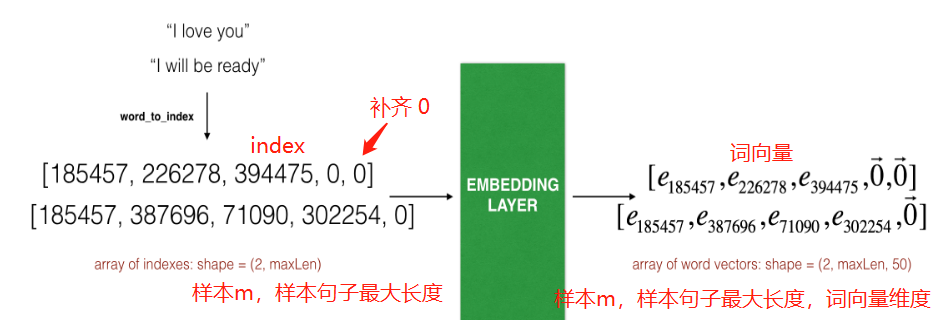
- 先把所有句子的單詞對應的 idx 填好
# GRADED FUNCTION: sentences_to_indices
def sentences_to_indices(X, word_to_index, max_len):
"""
Converts an array of sentences (strings) into an array of indices corresponding to words in the sentences.
The output shape should be such that it can be given to `Embedding()` (described in Figure 4).
Arguments:
X -- array of sentences (strings), of shape (m, 1)
word_to_index -- a dictionary containing the each word mapped to its index
max_len -- maximum number of words in a sentence. You can assume every sentence in X is no longer than this.
Returns:
X_indices -- array of indices corresponding to words in the sentences from X, of shape (m, max_len)
"""
m = X.shape[0] # number of training examples
### START CODE HERE ###
# Initialize X_indices as a numpy matrix of zeros and the correct shape (≈ 1 line)
X_indices = np.zeros((m, max_len))
for i in range(m): # loop over training examples
# Convert the ith training sentence in lower case and split is into words. You should get a list of words.
sentence_words = X[i].lower().split()
# Initialize j to 0
j = 0
# Loop over the words of sentence_words
for w in sentence_words:
# Set the (i,j)th entry of X_indices to the index of the correct word.
X_indices[i, j] = word_to_index[w]
# Increment j to j + 1
j = j+1
### END CODE HERE ###
return X_indices
實現 pretrained_embedding_layer()
- 初始化 詞嵌入矩陣,注意 shape
- 填充 詞嵌入矩陣,從
word_to_vec_map裡抽取 - 定義 Keras embedding 層,注意設定
trainable = False,使之不可被訓練,如果為True,則允許演演算法修改詞嵌入的值 - 將 嵌入權重 設定為與 嵌入矩陣 相等
# GRADED FUNCTION: pretrained_embedding_layer
def pretrained_embedding_layer(word_to_vec_map, word_to_index):
"""
Creates a Keras Embedding() layer and loads in pre-trained GloVe 50-dimensional vectors.
Arguments:
word_to_vec_map -- dictionary mapping words to their GloVe vector representation.
word_to_index -- dictionary mapping from words to their indices in the vocabulary (400,001 words)
Returns:
embedding_layer -- pretrained layer Keras instance
"""
vocab_len = len(word_to_index) + 1 # adding 1 to fit Keras embedding (requirement)
emb_dim = word_to_vec_map["cucumber"].shape[0] # define dimensionality of your GloVe word vectors (= 50)
### START CODE HERE ###
# Initialize the embedding matrix as a numpy array of zeros of shape (vocab_len, dimensions of word vectors = emb_dim)
emb_matrix = np.zeros((vocab_len, emb_dim))
# Set each row "index" of the embedding matrix to be the word vector representation of the "index"th word of the vocabulary
for word, index in word_to_index.items():
emb_matrix[index, :] = word_to_vec_map[word]
# Define Keras embedding layer with the correct output/input sizes, make it trainable. Use Embedding(...). Make sure to set trainable=False.
embedding_layer = Embedding(vocab_len, emb_dim, trainable=False)
### END CODE HERE ###
# Build the embedding layer, it is required before setting the weights of the embedding layer. Do not modify the "None".
embedding_layer.build((None,))
# Set the weights of the embedding layer to the embedding matrix. Your layer is now pretrained.
embedding_layer.set_weights([emb_matrix])
return embedding_layer
2.3 建立 Emojifier-V2
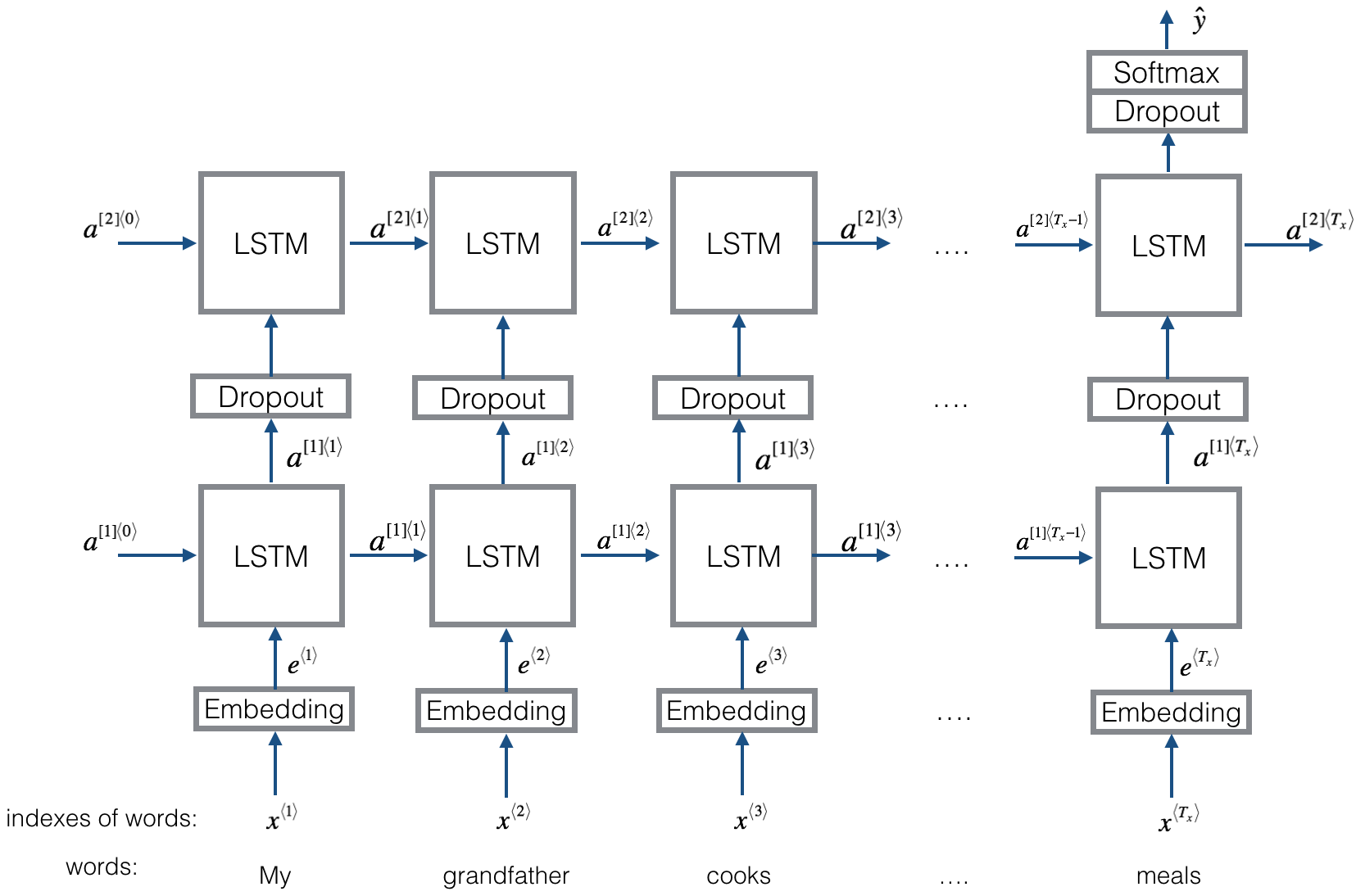
https://keras.io/zh/layers/core/
https://keras.io/zh/layers/embeddings/#embedding
https://keras.io/zh/layers/recurrent/
https://keras.io/zh/layers/core/
https://keras.io/zh/layers/core/
https://keras.io/zh/activations/
https://keras.io/zh/models/about-keras-models/
# GRADED FUNCTION: Emojify_V2
def Emojify_V2(input_shape, word_to_vec_map, word_to_index):
"""
Function creating the Emojify-v2 model's graph.
Arguments:
input_shape -- shape of the input, usually (max_len,)
word_to_vec_map -- dictionary mapping every word in a vocabulary into its 50-dimensional vector representation
word_to_index -- dictionary mapping from words to their indices in the vocabulary (400,001 words)
Returns:
model -- a model instance in Keras
"""
### START CODE HERE ###
# Define sentence_indices as the input of the graph, it should be of shape input_shape and dtype 'int32' (as it contains indices).
sentence_indices = Input(input_shape, dtype='int32')
# Create the embedding layer pretrained with GloVe Vectors (≈1 line)
embedding_layer = pretrained_embedding_layer(word_to_vec_map, word_to_index)
# Propagate sentence_indices through your embedding layer, you get back the embeddings
embeddings = embedding_layer(sentence_indices)
# Propagate the embeddings through an LSTM layer with 128-dimensional hidden state
# Be careful, the returned output should be a batch of sequences.
X = LSTM(128,return_sequences=True)(embeddings)
# Add dropout with a probability of 0.5
X = Dropout(rate=0.5)(X)
# Propagate X trough another LSTM layer with 128-dimensional hidden state
# Be careful, the returned output should be a single hidden state, not a batch of sequences.
X = LSTM(128, return_sequences=False)(X)
# Add dropout with a probability of 0.5
X = Dropout(rate=0.5)(X)
# Propagate X through a Dense layer with softmax activation to get back a batch of 5-dimensional vectors.
X = Dense(5)(X)
# Add a softmax activation
X = Activation('softmax')(X)
# Create Model instance which converts sentence_indices into X.
model = Model(inputs=sentence_indices, outputs=X)
### END CODE HERE ###
return model
- 建立模型
model = Emojify_V2((maxLen,), word_to_vec_map, word_to_index)
model.summary()
輸出:
Model: "model_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_3 (InputLayer) (None, 10) 0
_________________________________________________________________
embedding_4 (Embedding) (None, 10, 50) 20000050
_________________________________________________________________
lstm_3 (LSTM) (None, 10, 128) 91648
_________________________________________________________________
dropout_1 (Dropout) (None, 10, 128) 0
_________________________________________________________________
lstm_4 (LSTM) (None, 128) 131584
_________________________________________________________________
dropout_2 (Dropout) (None, 128) 0
_________________________________________________________________
dense_1 (Dense) (None, 5) 645
_________________________________________________________________
activation_1 (Activation) (None, 5) 0
=================================================================
Total params: 20,223,927
Trainable params: 223,877
Non-trainable params: 20,000,050 注:(400,001個單詞*50詞向量維度)
_________________________________________________________________
- 設定模型
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
- 訓練模型
轉換 X,Y 的格式
X_train_indices = sentences_to_indices(X_train, word_to_index, maxLen)
Y_train_oh = convert_to_one_hot(Y_train, C = 5)
訓練
model.fit(X_train_indices, Y_train_oh, epochs = 50, batch_size = 32, shuffle=True)
輸出:
WARNING:tensorflow:From c:\program files\python37\lib\site-packages\keras\backend\tensorflow_backend.py:422: The name tf.global_variables is deprecated. Please use tf.compat.v1.global_variables instead.
Epoch 1/50
132/132 [==============================] - 1s 5ms/step - loss: 1.6088 - accuracy: 0.1970
Epoch 2/50
132/132 [==============================] - 0s 582us/step - loss: 1.5221 - accuracy: 0.3636
Epoch 3/50
132/132 [==============================] - 0s 574us/step - loss: 1.4762 - accuracy: 0.3939
(省略)
Epoch 49/50
132/132 [==============================] - 0s 597us/step - loss: 0.0115 - accuracy: 1.0000
Epoch 50/50
132/132 [==============================] - 0s 582us/step - loss: 0.0182 - accuracy: 0.9924
在訓練集上的準確率幾乎 100%
- 在測試集上測試
X_test_indices = sentences_to_indices(X_test, word_to_index, max_len = maxLen)
Y_test_oh = convert_to_one_hot(Y_test, C = 5)
loss, acc = model.evaluate(X_test_indices, Y_test_oh)
print()
print("Test accuracy = ", acc)
輸出:
56/56 [==============================] - 0s 2ms/step
Test accuracy = 0.875
測試集上準確率為 87.5%
- 檢視預測錯誤的樣本
# This code allows you to see the mislabelled examples
C = 5
y_test_oh = np.eye(C)[Y_test.reshape(-1)]
X_test_indices = sentences_to_indices(X_test, word_to_index, maxLen)
pred = model.predict(X_test_indices)
for i in range(len(X_test)):
x = X_test_indices
num = np.argmax(pred[i])
if(num != Y_test[i]):
print('Expected emoji:'+ label_to_emoji(Y_test[i]) + ' prediction: '+ X_test[i] + label_to_emoji(num).strip())
輸出:
Expected emoji:😞 prediction: work is hard 😄
Expected emoji:😞 prediction: This girl is messing with me ❤️
Expected emoji:😞 prediction: work is horrible 😄
Expected emoji:🍴 prediction: any suggestions for dinner 😄
Expected emoji:😄 prediction: you brighten my day ❤️
Expected emoji:😞 prediction: go away ⚾
Expected emoji:🍴 prediction: I did not have breakfast ❤️
- 用自己的例子測試
# Change the sentence below to see your prediction. Make sure all the words are in the Glove embeddings.
x_test = np.array(['not feeling happy'])
X_test_indices = sentences_to_indices(x_test, word_to_index, maxLen)
print(x_test[0] +' '+ label_to_emoji(np.argmax(model.predict(X_test_indices))))
not feeling happy 😞 (這次 LSTM 可以預測 not 這類的組合詞了)
not very happy 😞
very happy 😄
i really love my wife ❤️
總結:
- 如果你有一個訓練集很小的NLP任務,使用單詞嵌入可以顯著地幫助你的演演算法。單詞嵌入允許模型處理測試集中沒有出現在訓練集中的單詞
- 在Keras(和大多數其他深度學習框架中)中訓練序列模型需要一些重要的細節:
- 要使用
mini-batches,需要填充序列,以便mini-batches中的所有樣本具有相同的長度 「Embedding()」層可以用預先訓練的值初始化。這些值可以是固定的,也可以在資料集中進一步訓練。如果資料集很小就不要接著訓練了(效果不大)LSTM()有一個名為「return_sequences」的標誌,用於決定是返回每個隱藏狀態還是只返回最後一個隱藏狀態- 可以在
LSTM()之後使用Dropout()來正則化網路
本文地址:https://michael.blog.csdn.net/article/details/108902060
我的CSDN部落格地址 https://michael.blog.csdn.net/
長按或掃碼關注我的公眾號(Michael阿明),一起加油、一起學習進步!