最佳化問題(一)
1. 最佳化問題
其實早在高中階段,我們就已經學習過了什麼是最佳化問題。
求一元二次方程 f ( x ) = x 2 + 2 ∗ x + 1 f(x)=x^2+2*x+1 f(x)=x2+2∗x+1 的最小值
求解方法也很簡單,令
f
(
x
)
f(x)
f(x) 對
x
x
x 的導數為0,該方程的解即為極值點。
現在我們知道,之所以可以這麼求解是因為函數
f
(
x
)
f(x)
f(x) 為凸函數,其極值點就對應最優解。同時
f
(
x
)
f(x)
f(x) 的導數方程可以直接求解的,但對於更為複雜的情形,就不一定能直接求解出來了。所以我們需要更為通用的求解方法。
2. 最佳化問題分類
要知道通用的最佳化問題求解方法,就需要了解最佳化問題的分類及一般形式。最佳化問題可以分為3個層次:最簡單的是無約束優化,其次是帶等式約束的優化,最難的是帶不等式約束和等式約束的優化。
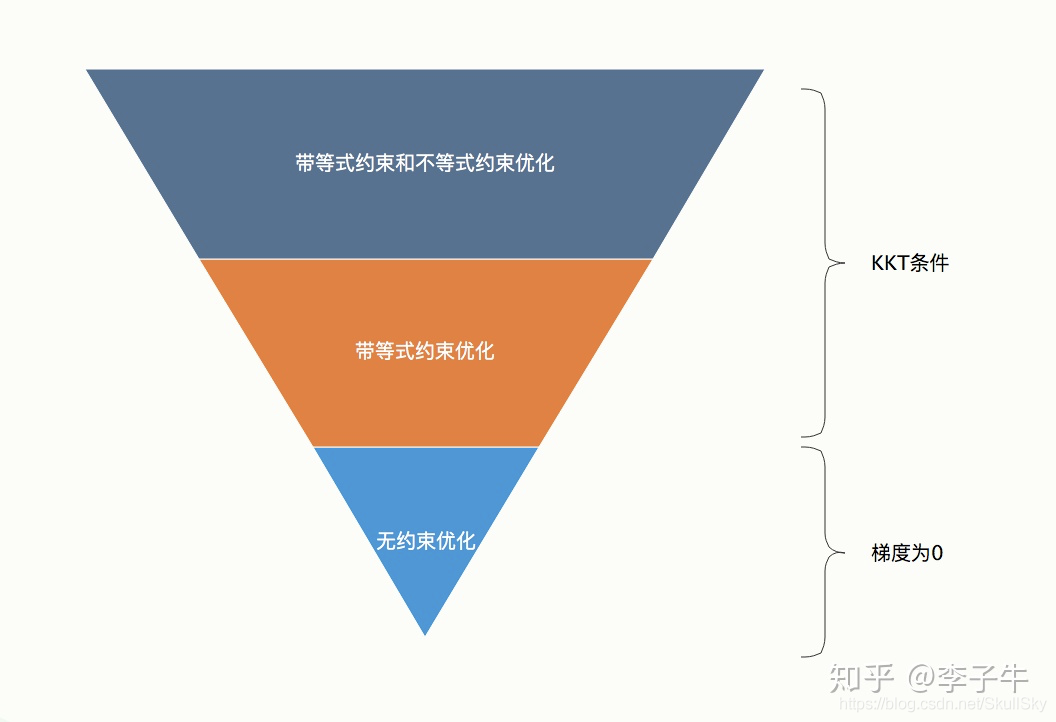
下面我們一一舉例介紹每個類別,
- 無約束優化:上面我們提到的一元二次方程最小值問題就是一個典型的無約束優化問題
- 等式約束優化:將上面的問題擴充一下,就變成了等式約束優化問題了
已知 x + y = 5 x+y=5 x+y=5 ,求二元二次方程 f ( x ) = x 2 + 2 ∗ y + 1 f(x)=x^2+2*y+1 f(x)=x2+2∗y+1 的最小值
- 不等式約束優化:將上面的問題再擴充一下,就變成了不等式約束優化問題了
已知 x + y > = 5 x+y>=5 x+y>=5 ,求二元二次方程 f ( x ) = x 2 + 2 ∗ y + 1 f(x)=x^2+2*y+1 f(x)=x2+2∗y+1 的最小值
由此,可以給出最佳化問題的一般形式:
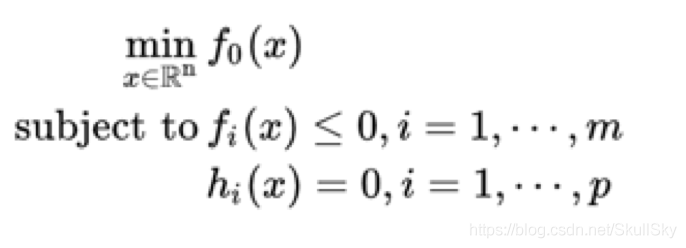

3. 最佳化問題求解
對於無約束優化問題,常見的方法有:梯度下降法、最速下降法、牛頓迭代法等;而在有約束的問題中,直接使用這些基於梯度的方法會有問題,如更新後的值不滿足約束條件。
那麼問題來了,如何處理有約束的優化問題?大致可以分為以下兩種方式(後面將一一介紹):
- 將有約束的問題轉化為無約束的問題,如拉格朗日乘子法和KKT條件、罰函數法;
- 對無約束問題下的求解演演算法進行修改,使其能夠運用在有約束的問題中,如對梯度下降法進行投影,使得更新後的值都滿足約束條件。
4. 最佳化問題的應用
最佳化問題在實際場景中十分常見,例如機器學習中很多模型的擬合過程就是一個優化問題,優化目標就是最小化損失函數。
-
無約束的最佳化問題
如線性迴歸的損失函數最小化目標(又稱為最小二乘法):
min 1 2 ∑ i = 1 m ( h ( x i ) − y i ) 2 \min \dfrac{1}{2} \sum_{i=1} ^m (h(x_i) - y_i)^2 min21∑i=1m(h(xi)−yi)2
如果在原始最小二乘法損失函數的基礎上加上正則化項,又變成了新的優化目標:
Lasso迴歸: min 1 2 ∑ i = 1 m ( h ( x i ) − y i ) 2 + λ ∑ j = 1 n ∣ ω j ∣ \min \dfrac{1}{2} \sum_{i=1} ^m (h(x_i) - y_i)^2 + \lambda \sum_{j=1} ^ n |\omega_j| min21∑i=1m(h(xi)−yi)2+λ∑j=1n∣ωj∣
嶺迴歸: min 1 2 ∑ i = 1 m ( h ( x i ) − y i ) 2 + λ ∑ j = 1 n ∣ ω j ∣ 2 \min \dfrac{1}{2} \sum_{i=1} ^m (h(x_i) - y_i)^2 + \lambda \sum_{j=1} ^ n |\omega_j|^2 min21∑i=1m(h(xi)−yi)2+λ∑j=1n∣ωj∣2
其中, λ \lambda λ 是正則化項的係數,用於權衡模型結構風險與經驗風險的比重,可以看到LASS迴歸於嶺迴歸的差別僅僅在於使用的正則化項而已,LASS使用的是L1正則化,嶺迴歸使用的是L2正則化。 -
有約束的最佳化問題
這一類優化問題除了有目標函數項,還有其他約束項。比如:SVM 的優化目標為最大化幾何間隔,即
max r = r ^ ∣ ∣ ω ∣ ∣ \max r = \dfrac{\hat{r}}{||\omega||} maxr=∣∣ω∣∣r^
其中, r r r 是樣本集合在樣本空間的最小几何間隔(幾何間隔:樣本點到分介面的垂直距離), r ^ \hat{r} r^是函數間隔,幾何間隔與函數間隔滿足 r = r ^ / ∣ ∣ ω ∣ ∣ r=\hat{r}/||\omega|| r=r^/∣∣ω∣∣ , ω \omega ω 是分界超平面的係數向量,SVM的目標就是要讓上圖中的r最大化。
但是,這個優化目標還要滿足額外的約束條件:
r i > = r r_i >= r ri>=r
其中, r i r_i ri 表示每個樣本各自的幾何間隔,很顯然最小的幾何間隔肯定要小於等於每個樣本各自的幾何間隔。
則,完整的優化目標可以寫成:
max r \max r maxr, s.t. r i = y i ( w x i + b ) ∣ ∣ ω ∣ ∣ = r i ^ ∣ ∣ ω ∣ ∣ > = r r_i=\dfrac{y_i(wx_i+b)}{||\omega||}=\dfrac{\hat{r_i}}{||\omega||} >= r ri=∣∣ω∣∣yi(wxi+b)=∣∣ω∣∣ri^>=r
兩邊同時乘以 ∣ ∣ ω ∣ ∣ ||\omega|| ∣∣ω∣∣,
max r \max r maxr, s.t. y i ( w x i + b ) > = ∣ ∣ ω ∣ ∣ r y_i(wx_i+b)>=||\omega||r yi(wxi+b)>=∣∣ω∣∣r
由 r = r ^ / ∣ ∣ ω ∣ ∣ r=\hat{r}/||\omega|| r=r^/∣∣ω∣∣,
max r ^ ∣ ∣ ω ∣ ∣ \max \dfrac{\hat{r}}{||\omega||} max∣∣ω∣∣r^, s.t. y i ( w x i + b ) > = r ^ y_i(wx_i+b)>=\hat{r} yi(wxi+b)>=r^
為了簡化優化目標,令 r ^ = 1 \hat{r}=1 r^=1 ,,則完整的優化目標可以寫成:
max 1 ∣ ∣ ω ∣ ∣ \max \dfrac{1}{||\omega||} max∣∣ω∣∣1, s.t. y i ( w x i + b ) > = 1 , i = 1 , 2... , n y_i(wx_i+b)>=1,i=1, 2...,n yi(wxi+b)>=1,i=1,2...,n