排序演演算法

氣泡排序

簡單選擇排序

直接插入排序

希爾（shell）排序

快速排序

歸併排序

歸併排序

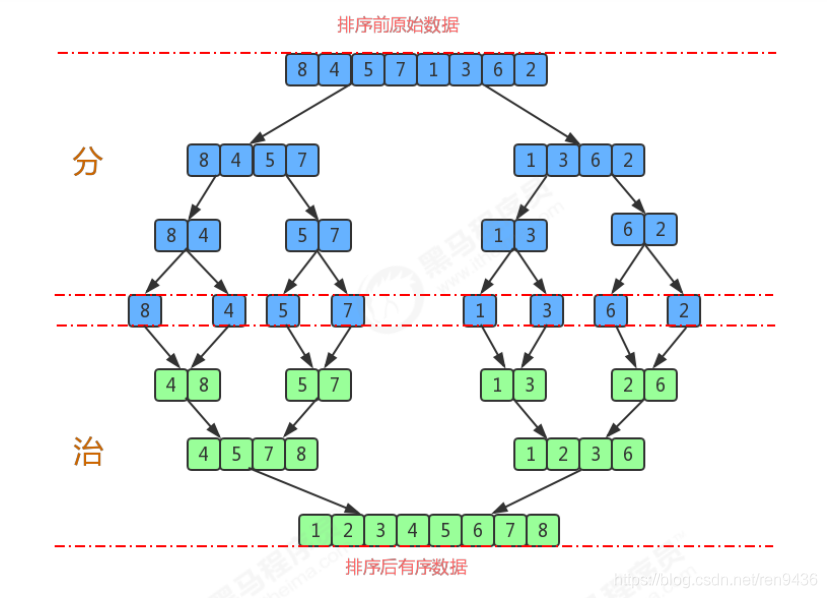
排序原理：

1. 儘可能的將一組資料拆分成兩個元素相等的子組，並對每一個子組繼續拆分，直到拆分後的每個子組的元素個數是1為止。
2. 將相鄰的兩個子組進行合併成一個有序的大組；
3. 不斷的重複步驟2，直到最終只有一個組為止。

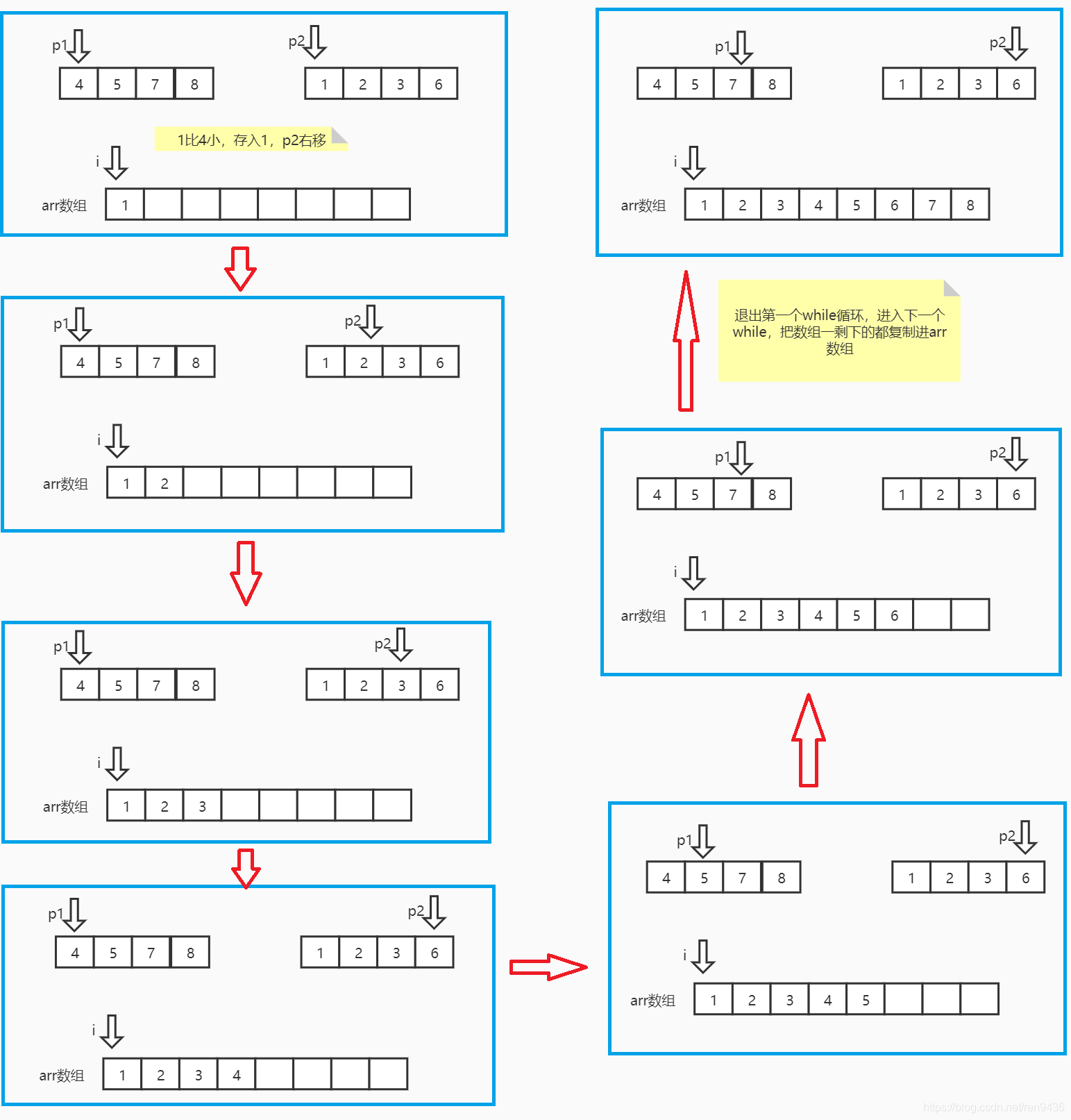
對最後合併細化分析，核心程式碼Merge

Java程式碼

import java.util.Arrays;
public class MergeSort {

    private static int[] arr;
    public static void sort(int[] a){
        arr = new int[a.length];
        sort(a,0,a.length-1);
    }

    private static void sort(int[] a,int lo, int hi){
        if(lo>=hi) return;
        int mid = lo + (hi - lo)/2;
        sort(a,lo,mid);
        sort(a,mid+1,hi);
        //合併兩個陣列
        merge(a,lo,mid,hi);
    }
    private static void merge(int[] a, int lo,int mid ,int hi ){
        //指向輔助陣列的指標。
        int i = lo;
        //定義第一個陣列的指標，初始指向第一個元素；
        int p1 = lo;
        //定義第二個陣列的指標，初始指向第一個元素
        int p2 = mid+1;

        //比較兩個陣列指標指向的元素的大小，哪個小，就放入arr陣列
        while(p1<=mid&&p2<=hi){
            if(a[p1]<a[p2]){
                arr[i++]=a[p1++];
            }else{
                arr[i++]=a[p2++];
            }
        }
        //如果陣列二遍歷完，陣列一沒完
        while(p1<=mid){
            arr[i++] = a[p1++];
        }
        //如果陣列一遍歷完，陣列二沒完
        while(p2<=hi){
            arr[i++] = a[p2++];
        }

        //拷貝陣列
        for (int i1 = lo; i1 <= hi; i1++) {
            a[i1] = arr[i1];
        }

    }

    public static void main(String[] args) {
        int[] a = {8, 4, 5, 7, 1, 3, 6, 2};
        sort(a);
        System.out.println(Arrays.toString(a));
    }

}

演演算法複雜度分析

O(nlogn)

歸併排序是分治思想的最典型的例子，上面的演演算法中，對a[lo…hi]進行排序，先將它分為a[lo…mid]和a[mid+1…hi]
兩部分，分別通過遞迴呼叫將他們單獨排序，最後將有序的子陣列歸併為最終的排序結果。該遞迴的出口在於如果
一個陣列不能再被分為兩個子陣列，那麼就會執行merge進行歸併，在歸併的時候判斷元素的大小進行排序。

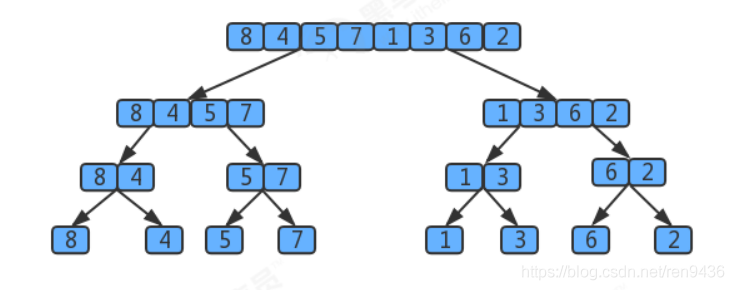
用樹狀圖來描述歸併，如果一個陣列有8個元素，那麼它將每次除以2找最小的子陣列，共拆log8次，值為3，所以樹共有3層,那麼自頂向下第k層有2^k個子陣列，每個陣列的長度為2^(3-k)，歸併最多需要2^(3-k)次比較。因此每層的比較次數為 2^k * 2^(3-k)=2^3,那麼3層總共為 3*2^3。

假設元素的個數為n，那麼使用歸併排序拆分的次數為log2(n),所以共log2(n)層，那麼使用log2(n)替換上面32^3中 的3這個層數，最終得出的歸併排序的時間複雜度為：log2(n) 2^(log2(n))=log2(n)*n,根據大O推導法則，忽略底數，最終歸併排序的時間複雜度為O(nlogn).

歸併排序需要申請額外的陣列空間，導致空間複雜度提升，是典型的以空間換時間的操作。

穩定性

穩定的

歸併排序在歸併的過程中，只有arr[i]<arr[i+1]的時候才會交換位置，如果兩個元素相等則不會交換位置，所以它
並不會破壞穩定性，歸併排序是穩定的。