資料庫正規化

今天剛好回憶下正規化，參考這篇 如何理解關係型資料庫的常見設計正規化？ 文章，我在此文章進一步改進。

什麼是正規化？

教材書這樣定義：符合某一種級別的關係模式的集合，表示一個關係內部各屬性之間的聯絡的合理化程度。

實話實說，真不懂！！然後看了博主的文章解釋的很好。也就可以理解為：一張資料表的表結構所符合的某種設計標準的級別。就比如王者榮耀的VIP，有VIP1，VIP2，VIP3等等，VPI2是基於VIP1而來的，而不是直接跳過VIP1直到VIP2，所以VIP1的獎勵也可以領取。那麼資料庫正規化也分為1NF，2NF，3NF，4NF，5NF。還有一種是BCNF，對於3NF進一步改進。

一般而已，對於資料庫的設計，滿足第三正規化或者BC正規化就足夠了。

第一規格化（1NF）

第一規格化是對關係模型的最基本的要求，其定義就是資料庫表的每一列都是不可再分割的。

舉正例可能看不清楚，舉個反例：

如上圖，學生、系、課程這些列還可以再分，所以上表不滿足第一規格化，只要不滿足第一規格化的表都不是關係型資料庫表。

正確的做法是：（順便插入幾條記錄）

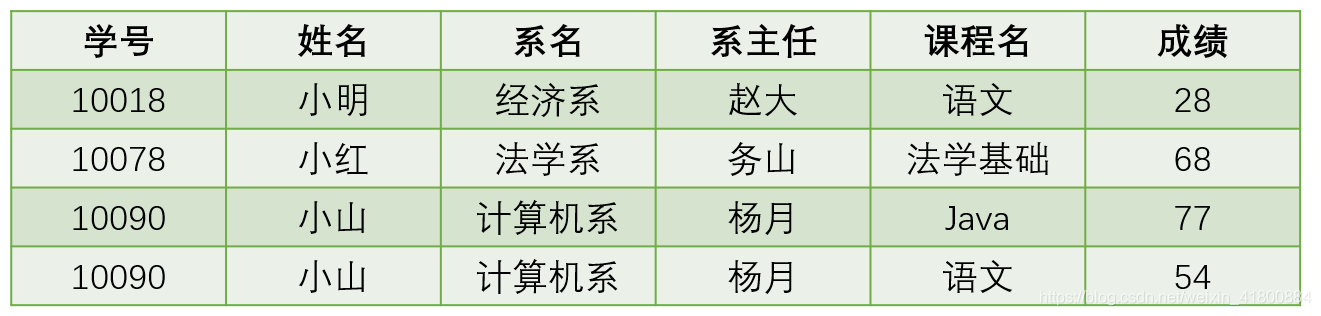
僅僅滿足第一規格化還是存在很多問題，比如資料冗餘過大，插入異常，刪除問題，修改冗餘的問題。

• 資料冗餘過大：一張表中，每個學生的學號，姓名，還有系名，系主任重複出現。
• 插入異常：假設新建一個系，那麼這個系的資訊在還沒學生前不能提前錄入表中，因為沒有主鍵。

注１：根據三種關係完整性約束中實體完整性的要求，關係中的碼（注２）所包含的任意一個屬性都不能為空，所有屬性的組合也不能重複。為了滿足此要求，圖中的表，只能將學號與課名的組合作為碼，否則就無法唯一地區分每一條記錄。

注２：碼：關係中的某個屬性或者某幾個屬性的組合，用於區分每個元組（可以把「元組」理解為一張表中的每條記錄，也就是每一行）。

• 刪除問題：假設某個系的學生都沒有了，刪除後那麼該系的資訊也都沒有了。實際上，雖然沒有學生了，但不代表這個系不存在。
• 修改冗餘：假設某個學生轉系，那麼就得修改他的系資訊，而且還得修改多次，比如上面的小山轉系，那麼得修改2次。

所以為了解決這些問題，出現了第二正規化。

注：屬性是否真的不可拆分，根據你的設計目標而定，比如說姓名，是否還得繼續拆為性和名呢？看自己。

第二正規化（2NF）

要了解第二正規化，需要一些前置知識：

函數依賴

定義：若在一張表中，在屬性（或屬性組）X 的值確定的情況下，必定能確定 屬性Y 的值，那麼就可以說：Y函數依賴於X，記作 X -> Y。

比如上面的表，通過學號就可以確定姓名（一條記錄），那麼說明：姓名 依賴於 學號；而通過姓名不一定能確定學號（多條記錄），因為可能有同名，說明：學號 不依賴於 姓名。

大白話：知道某屬性值就可以唯一確定另一屬性的值。

完全函數依賴

定義：如果非主屬性B函數依賴於構成某個候選關鍵字的一組主屬性A，而且A的任何一個真子集不能被B函數依賴，則稱B完全函數依賴於A。如果已經確定就一個主屬性，那麼可以肯定其他屬性完全依賴於該主屬性。

比如上面的表，通過學號和課程名就可以確定成績（僅學號或者課程名不能查出成績），所以成績完全函數依賴於學號和課程名。

大白話：通過一個屬性值，能唯一確定某值，如果是屬性組，那麼該屬性組中必須所有屬性組合在一起才能確定某屬性值。

部分函數依賴

定義跟上面相反了，定義：若B函數能依賴於A的真子集，則稱B部分函數依賴於A。

比如上面的表，通過學號和課程名可以確定姓名，但是單單通過學號也可以確定姓名，所以姓名部分依賴於學號和課程名。

大白話：僅對於屬性組來說，如果屬性組中不需要所有屬性組合在一起就能確定某值。

傳遞函數依賴

定義：在 Y 不包含於 Z 且 Y 不函數依賴於 X，假設 Z函數依賴於Y，且Y函數依賴於X，那麼就稱Z傳遞函數依賴X。

比如上面的表，通過學號可以查出系名，通過系名可以查出系主任，所以通過學號可以查出系主任，所以稱系主任傳遞函數依賴於學號。

超關鍵字/超鍵/超碼/碼

定義：能夠唯一標識一條記錄的屬性或屬性集。

比如上面的表，通過學號可以查出系名，通過學號和姓名也可以查出系名類似這樣的，可以說包含該學號的任意屬性組合都是超鍵。

候選碼/候選鍵

定於：若關係中的一個屬性或屬性組的值能夠唯一地標識一個元組（就是一條記錄），且他的真子集不能唯一的標識一個元組（完全函數依賴），則稱這個屬性或屬性組做候選碼。或者說：能夠唯一標識一條記錄的最小屬性組。

比如上面的表，可以通過學號確定某個屬性的值，但是對於成績，僅僅使用學號不夠，還得有課程名才可能獲取成績，其實對於課程名單單使用學號也無法確定。所以對於 學號 和 課程名 這個屬性組就是候選碼。而通過學號和姓名可以確定系名，但是單單通過學號也可以確定，而姓名是多餘的，所以姓名不是候選碼。

主鍵

當有多個候選碼時，可以從候選碼中選取一個/或一組作為主鍵。

比如上面的的表，要唯一確定一條記錄，那麼得知道 學號 和 課程名，而這兩個都得作為主鍵。

主屬性

在候選碼中挑選，比如候選碼為：(A，B)，（A，C）。那麼主屬性為A，B，C。

非主屬性

包含在任何一個候選碼中的屬性成為主屬性。那麼非主屬性也就知道了。

比如上面的表，已經確定 學號 和 課程名 這個屬性組就是候選碼，那麼 學號 和 課程名 都是主屬性，那麼其他屬性就都是非主屬性。

---

那麼第二正規化的定義是：在滿足第一規格化的前提下，是否存在非主屬性對於候選碼的部分函數依賴或者說對於所有的非主屬性是完全函數依賴於候選碼。若存在，則資料表最高只符合1NF的要求，若不存在，則符合2NF的要求。（大白話：找主鍵，能夠確定某列的值，但是如果有多個主鍵，看看這些主鍵還要不要拆分，判斷條件：這些主鍵能夠確定某列A的值並且不存在這些主鍵中其中一個就能確定某列A值）

判斷的方法是：

• 第一步：找出資料表中所有的候選碼。
• 第二步：根據第一步所得到的碼，找出所有的主屬性。
• 第三步：資料表中，除去所有的主屬性，剩下的就都是非主屬性了。
• 第四步：檢視是否存在非主屬性對候選碼的部分函數依賴。

例子：

• 第一步：
  • 檢視所有每一單個屬性，當它的值確定了，是否剩下的所有屬性值都能確定。
  • 檢視所有包含有兩個屬性的屬性組，當它的值確定了，是否剩下的所有屬性值都能確定。
  • ……
  • 檢視所有包含了六個屬性，也就是所有屬性的屬性組，當它的值確定了，是否剩下的所有屬性值都能確定。
  • 有一個訣竅（參考的答主說的）：如果A是候選碼，那麼所有包含A的屬性組就不是碼了，因為碼要求除碼之外的所有屬性都完全函數依賴於碼。但是上面的表，通過學號可以查詢姓名，也可以通過學號和系名查詢姓名或者學號和系主任查詢姓名，那麼很明顯，系名或者系主任並不是碼，而學號是碼，這符合答主說的。但是單單使用學號，不能查出課程名和成績，所以除了學號作為碼，還得需要課程名作為碼，通過學號和課程名屬性組作為碼才可以查出成績。所以我認為答主的說法太絕對了，應該這樣說：如果A是碼，並且包含A的屬性組都可以查詢某屬性值，那麼說明該包含A的屬性組不是碼，但是如果包含A的屬性組能夠確定單單A查詢不到的某列值，那麼說明包含A的屬性組也是碼。（不知道這樣理解對不對…）
• 第二步：第一步已經分析出候選碼：學號、課程名。那麼它們都是主屬性。
• 第三步：知道了主屬性，那麼剩下的都是非主屬性：姓名，系名，系主任，成績。
• 第四步：
  • （學號，課程名）-> 姓名，但 學號 -> 姓名，所以存在非主屬性對於候選碼的部分函數依賴。
  • （學號，課程名）-> 系名，但 學號 -> 系名，所以存在非主屬性對於候選碼的部分函數依賴。
  • （學號，課程名）-> 系主任，但 學號 -> 系主任，所以存在非主屬性對於候選碼的部分函數依賴。
  • （學號，課程名）-> 成績，非主屬性對於候選碼的完全函數依賴。

所以上表不滿足第二正規化。那麼需要對錶進行拆分，根據上面的分析，可以拆分為：

• 成績表（學號，課程名，成績）
• 學生表（學號，姓名，系名，系主任）

現在重新分析這樣是否滿足第二正規化：

• 成績表：學號和課程名是候選鍵，也就是主屬性，成績是非主屬性。單單通過學號或者課程名都查不出成績，所以可以發現不存在非主屬性對於候選碼的部分函數依賴，滿足第二正規化。
• 學生表：學號是候選鍵，也是主屬性，姓名、系名、系主任是非主屬性。因為候選碼只有一個，所以可以確定不存在非主屬性對於候選碼的部分函數依賴，滿足第二正規化。

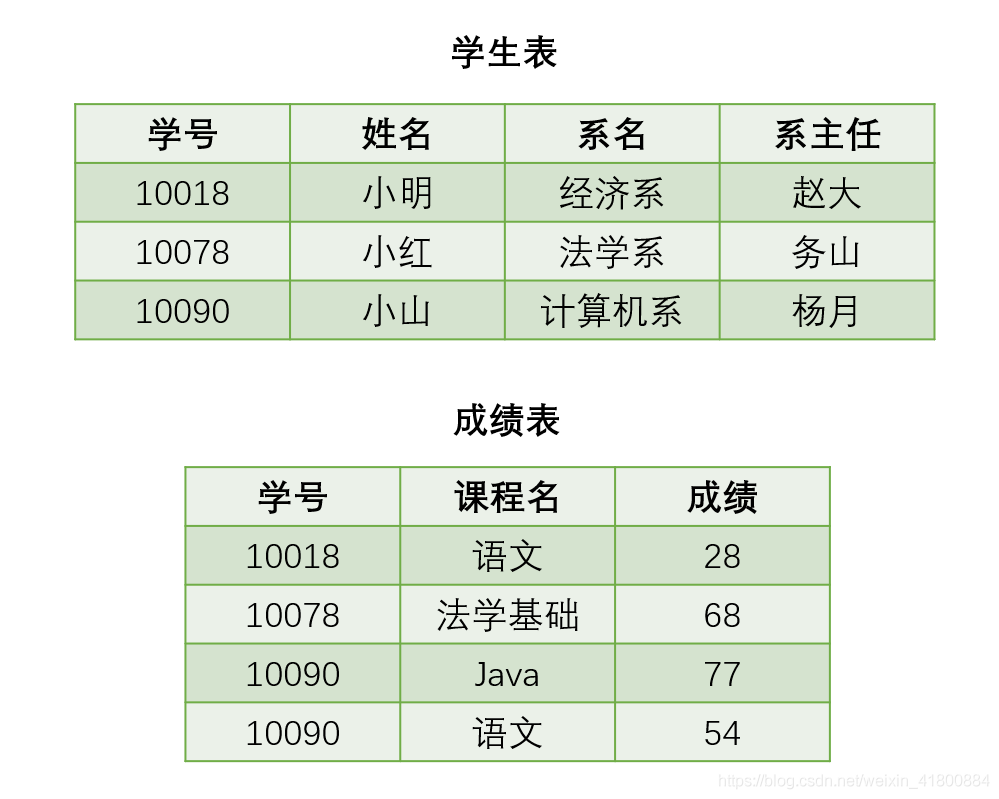
現在來看看第一規格化存在的問題是否解決：

• 資料冗餘過大：有所改進，但是比如還有多個計算機系的學生，那麼系名和系主任兩個列還是重複出現。

• 插入異常：假設新建一個系，那麼這個系的資訊在還沒學生前不能提前錄入表中，因為沒有主鍵。還存在該問題。

• 刪除問題：假設某個系的學生都沒有了，刪除後那麼該系的資訊也都沒有了。實際上，雖然沒有學生了，但不代表這個系不存在。還存在該問題。

• 修改冗餘：假設某個學生轉系，那麼就得修改他的系資訊，而且還得修改多次，比如上面的小山轉系，那麼得修改2次。已經解決，因為可以保證學生表中每位學生只出現一次，所以轉系時只需要改一次。

所以在第二正規化的基礎上，提出了第三正規化來解決這些問題。

第三正規化（3NF）

定義：在第二正規化的基礎上，消除了非主屬性對於候選碼的傳遞函數依賴。也就是說：要求資料庫表中不包含其他表的非關鍵字資訊（消除冗餘的列，或者說非主鍵外的所有欄位必須互不依賴）。

分析上面的倆張表：

• 成績表：主屬性為學號和課程名，非主屬性為成績，不存在非主屬性對候選碼的傳遞函數依賴，滿足第三正規化。
• 學生表：主屬性為學號，非主屬性為姓名、系名和系主任。通過學號可以查出系主任，通過系名可以查出系主任，存在非主屬性對候選碼的傳遞函數依賴，不滿足第三正規化。

改進學生表：把學校資訊和系資訊拆分成兩張表：

• 系表（系名，系主任）
• 學生表（學號，姓名，系名）

不分析了，很容易看得出滿足第三正規化。

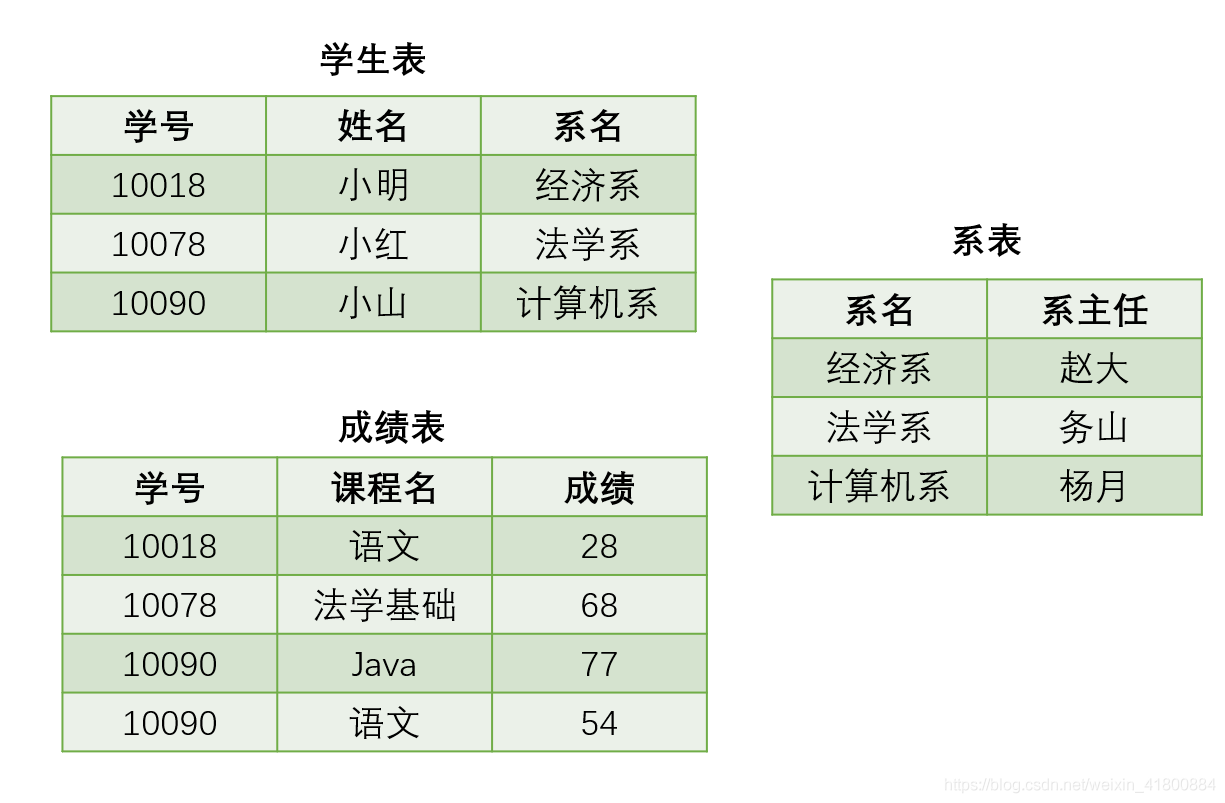
現在來看看之前的問題是否解決：

• 資料冗餘過大：已經解決。每位學生肯定還得對於一個系名，但至少系主任不會重複出現。

• 插入異常：假設新建一個系，可以直接錄入系表。已經解決。

• 刪除問題：假設某個系的學生都沒有了，刪除後，該系的資訊還可以存在，除非真要刪除該系資訊。已經解決。

BC正規化（BCNF）

定義：在滿足第三正規化的基礎上，消除主屬性對於候選碼的部分與傳遞函數依賴。（大白話：在多個主屬性中，消除多餘主屬性）

是對於第三正規化的改進，上面的第三正規化都沒問題的，為什麼還得改進？來看看特殊情況：

1. 某公司有若干個倉庫；
2. 每個倉庫只能有一名管理員，一名管理員只能在一個倉庫中工作；
3. 一個倉庫中可以存放多種物品，一種物品也可以存放在不同的倉庫中。每種物品在每個倉庫中都有對應的數量。

那麼關係模式 倉庫（倉庫名，管理員，物品名，數量） 屬於哪一級正規化？分析一波：

• 已知函數依賴集：倉庫名 -> 管理員，管理員 -> 倉庫名，（倉庫名，物品名）-> 數量
• 候選碼：倉庫名、管理員、物品名
• 非主屬性：數量

可以發現滿足第一規格化，並且不存在非主屬性部分函數依賴和傳遞函數依賴於候選碼，所以滿足第三正規化。

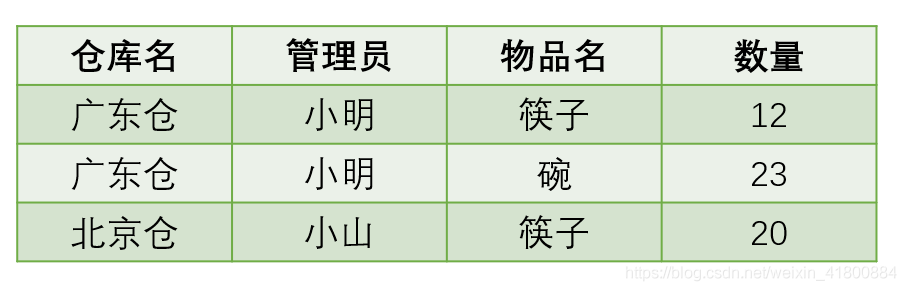
雖然滿足第三正規化，但看看有什麼問題存在：

• 假設要為一個倉庫換管理員，那麼在上表中可能得修改多次。出現資料冗餘。
• 如果新增一個倉庫，但尚未放入物品，是否可以指派管理員？不可以，因為物品名也是主屬性，得遵守實體完整性約束。
• 如果一個倉庫被清空後，需要刪除所有與該倉庫有關的物品存放記錄，那麼倉庫本身和管理員也會隨著刪除。

所有雖然滿足了第三正規化，但該表不是一個很好，主要的原因在於：存在著主屬性對於候選碼的部分函數依賴與傳遞函數依賴。也就是：倉庫名 對於 管理員、物品名 存在部分函數依賴與傳遞函數依賴：

• 部分函數依賴：通過管理員和物品名可以確定倉庫名，通過管理員可以確定倉庫名 或者 通過倉庫名和物品名可以確定管理員，通過倉庫名可以確定管理員。
• 傳遞函數依賴：倉庫名和物品名可以確定數量，而倉庫名可以確定管理員，那麼管理員和物品名也可以確定數量。（多餘主屬性）

如何解決？拆表：

• 倉庫表（倉庫名，管理員）
• 存庫表（倉庫名，物品名，數量）

可以發現上面存在的問題可以解決。

總結

第一規格化：資料庫表中的屬性（或者欄位或者列）不可再分割。

第二正規化：在滿足第一規格化的前提下，找主鍵，能夠確定某列的值，但是如果有多個主鍵，看看這些主鍵還要不要拆分，判斷條件：這些主鍵能夠確定某列A的值並且不存在這些主鍵中其中一個就能確定某列A值

第三正規化：在滿足第二正規化的前提下，消除冗餘的列，或者說非主鍵外的所有欄位必須互不依賴。

BC正規化：在滿足第三正規化的前提下，在多個主屬性中，消除多餘主屬性。

最好理解正規化中出現的問題。並且正規化並不是需要絕對遵守的準則，就像姓名這個欄位，可能不需要繼續拆分，可能需要拆為性和名兩個欄位。

有錯請指出