LSQ+: Improving low-bit quantization through learnable offsets and better
initialization
from Qualcomn AI Research | Seoul National University
CVPR2020
LSQ+：通過學習偏移和更好的初始化改進LSQ

Abstract

新的啟用函數，如Swish，Mish不像ReLU只有非負值，而是有正有負，而傳統的無符號量化策略會將所有負的啟用值量化為0，從而導致效能的顯著下降；如果為了對負啟用值也進行量化就需要增加額外的符號位，在低位元量化（2、3、4bit)中代價太大了。


為了解決這一問題，本文基於LSQ提出了改進版的LSQ+，通過引入一種通用的非對稱的量化策略，通過訓練學習縮放尺度scale和偏移引數offset，從而解決負啟用值的量化問題；另一方面基於梯度學習的量化方案訓練過程通常不穩定，因此需要調整大量的超引數才能達到較好的效能，LSQ+通過對待量化的引數使用MSE初始化策略有效緩解了這一問題，使得多次訓練結果的差異波動明顯降低。



在EfficientNet和MixNet上使用LSQ+的量化策略的表現要優於Swish啟用的LSQ低位元量化，比如EfficientNet的W4A4量化精度提升1.8%,EfficientNet的W2A2量化提升5.6%。據我們所知，這也是第一份將上述網路量化到如此低位數的工作。




其中WxAx表示將網路中的權重和啟用值量化為x位。

Section I Introduction

隨著深度神經網路在各種場景下得到了廣泛應用，相應對資源受限的硬體平臺上高效部署這些網路的需求也越來越大。嘗試的策略由網路剪枝、網路結構搜尋以及手動設計更為高效的網路結構（如深度可分離折積、SE模組等），本文通過將模型中的權重和啟用量化到較低位元，從而實現定點推理，減少記憶體頻寬的使用。




在這一過程中，也提出了一系列新的啟用函數，如Swish,H-swish,Leaky-ReLU作為Relu的替代，這些啟用函數會產生負的啟用值；而目前的量化方案，如PACT，LSQ使用的是無符號的量化範圍，因此所有小於0的啟用值都會被丟棄，量化為0.這種量化策略對使用ReLU作為啟用函數的網路如ResNet是十分使用的，但如果遷移到EfficientNet、MixNet這種使用新型啟用函數Swish的網路時就會導致嚴重的精度損失。




比如LSQ W4A4量化預訓練ResNet50幾乎不損失精度，然而在EfficientNet-B0中卻會導致4.1%的精度下降，因此單純使用有符號的量化範圍會導致效能的下降;如果量化範圍包含負值，則由於負值區域的值相對於正值而言更少，這樣會降低正值範圍內的表現能力。





為了緩解低位元量化這一精度下降問題，本文提出了一種通用的通過學習偏移引數和縮放引數的非對稱量化策略，更適合於負的啟用值的量化。





另一個問題是基於梯度學習的量化方法其訓練不穩定的問題，對初始化結果非常敏感，因此本文使用基於MSE（均方誤差的初始化來緩解這一問題。





總而言之，本文在LSQ的基礎上增加了對啟用值量化的偏移引數的學習，從而抵消量化過程中的精度損失；本文的實驗還表明了合理初始化對穩定訓練的重要性，尤其在低位元領域。

Section II Related Work

Paper16對量化的基礎知識做了很好的總數，主要解釋了對稱量化和非對稱量化的區別；通常可以將量化策略分為無需微調的訓練後的方法（post_training)以及需要微調的量化感知方法（quantization-aware).





Post-training方法無需網路完全訓練，而是基於少量資料進行優化，這類方法在傳統的8bit量化上有較好的實現，但在低位元量化中效果不佳。






Quantization-aware方法如果時間充足可以在低位元量化時優化至更好的精度，LSQ就是這類的代表之一，本文也是基於這類方法，但增添了新的量化和初始化的內容進去。







在調研過程中還發現有的工作致力於藉助知識蒸餾來提升量化效果、或者自動學習量化的位寬；而本文的工作與上述研究是正交的，也就是可以共同使用共同提升量化效果。

Section III Method

在LSQ中提出了一種具有學習可變步長的對稱量化方案，通過學習擴充套件引數scale完成對權重和啟用值的量化。

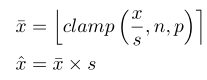
其中n.p由量化位數決定，量化後的值會被鉗制在n,p範圍內，如


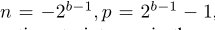
但無法處理activation有負數的情況，如Swish、Leaky ReLU,會導致精度下降；因此LSQ+對啟用使用的是非對稱量化策略。


Part A Learnable asymmetric quantization

由於權重引數一般在0附近對稱分佈的，所以憑經驗可以使用對稱量化，而啟用值使用費對稱量化。
本文提出的啟用值非對稱量化方案不僅需要學習尺度引數scale還考慮了偏移引數offset-betha

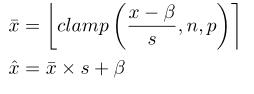
這一引數的梯度求導為：


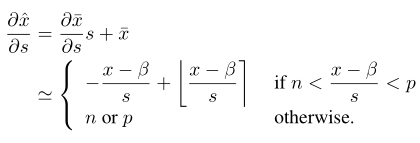
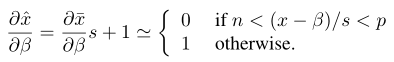
額外增加的偏移項增加了計算但是可以在編譯時預先計算好作為一項bias，到時候直接加入到計算中。

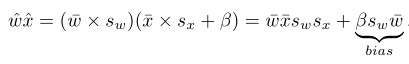
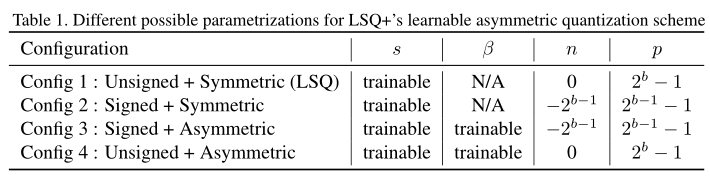
Table I展示了LSQ+非對稱量化的4種方案，其中Config1和Config2未加入偏移引數iffsert項，是基於LSQ的量化方式，只不過範圍不同；Config3和Config4則加入了可訓練引數offset項。

Part B Initialization of quantization parameters


前文提到在低位元量化中使用quantization-aware方式，在訓練過程中極不穩定，很容易受到初始化結果的影響。這一問題在計算深度可分離折積時會進一步放大，因此本文提出了一種新的對可訓練引數初始化的方法。


Scale initialization for weight quantization



對權重的scale引數LSQ使用的是符號對稱量化:

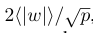
因此權重量化時沒有offset偏移引數的參與，但在2、3、4bit量化時收斂效果並不好；因此本文使用權重分佈的統計特徵-權重絕對值分佈的均值和方差，而不是真實的權重值來進行初始化：

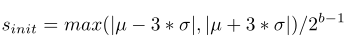
Scale/Offset initialization for activation quantization





Xmin和Xmax分別代表啟用值的最大和最小值，比如ReLU啟用函數的最小值Xmin=0，Swish的最小值Xmin=-0.278。
確定Xmin和Xmax，以及量化範圍的上下界皆可以得到scale和offset引數-beta的初始值：

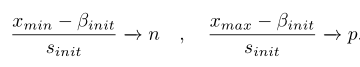
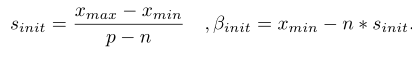
但是這種初始化計算方法很容易受到異常點的影響，這一問題通過先取幾個patch的資料，最小化MSE來進行優化，糾正初始值。



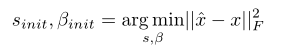
Section IV Experiments

本文在Swish啟用上進行W2A2,W3A3,W4A4量化測試LSQ+的效果，也是據我們所知第一次將本文使用的框架量化到如此低的位數。比較時還是保持了LSQ中傳統框架使用ReLU的精度進行對比，在所有的實驗設定中權重引數首先都被初始化為預訓練後的浮點數，主要對比使用不同的量化策略對效能的影響。

Part A Swish Activation 


Table 2和Table 3展示了基於EfficiNet-B0和MixNet-S框架下不同量化方案、量化不同位數後的效能對比。可以看到在W4A4量化時，offset引數的加入使得效能提升了1.6%、1.3%,而在W2A2中提升效果更明顯；


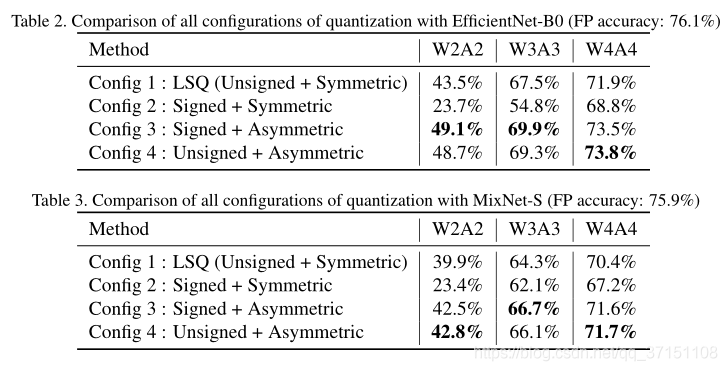
另外一個有意思的實驗結果是Config2(Signed+Symmetric)設定下的量化結果是最差的，首先沒有offseta引數，其次只有一半的量化範圍用於正啟用值的表示，而實際Swish函數中負數僅佔很少一部分，大部分是正啟用值，而量化範圍又減少了一半，因此表現力不足。

Part B ReLU Activation


Table 4則展示了本文四種量化方案與其他研究使用的量化方案對ResNet18中ReLU量化的結果對比，可以看到比ResNet的精度還要提升0.4-0.6%，在W4A4中都能達到70.7%的精度，而全精度的ResNet-18精度才為70.1%;同時也能看出LSQ+四種設定方案中沒有明顯的差距，也可以理解，因為ReLU啟用函數沒有負值,因此量化效果差別不大。


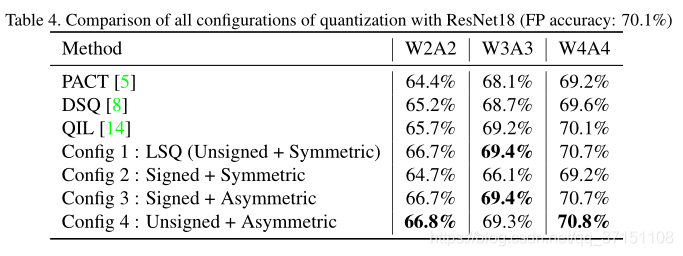
Part C Effect of quantization parameter initialization

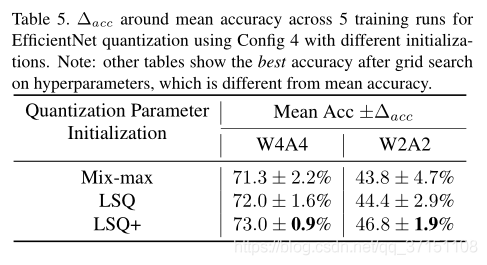
本文還對比了3種初始化方法的效果，其中前兩種設定沒有使用offset引數，一個是計算每一層權值或啟用值的最大最小值來獲得s初始值；一個是LSQ的初始化方案；
第三種則是LSQ+中引入offset引數的初始化方案。


量化方案則選擇的是基於EfficientNet-B0 Config4.通過Table5的對比結果可以看出Config3初始化後具有更好的穩定性，尤其是W2A2量化時，主要就是因為2bit量化是scale引數很容易受到權重或啟用值波動的影響，即使是LSQ的初始化方案也不可避免有一個很大的方差。

Section V Discussion

Part A Learned Offset Values

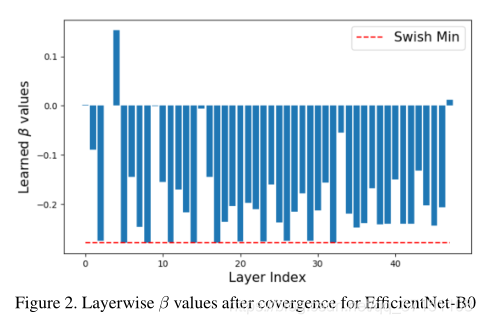
Fig2視覺化了每一層學到的offset偏移引數，基於在EfficientNet做W4A4量化，可以看到大多數offset引數都是負的，意味著啟用值在scale前就被平移了一部分，這意味著量化的層開始逐漸去調整負的啟用值。


Part B Learned Offset vs Fixed Offset

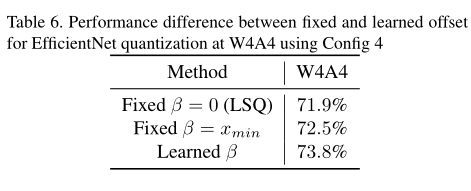
究竟是固定偏移量好呢還是學習可變的偏移量效果更佳呢，通過前一小節的觀察發現，學習到的offset量絕大部分都還沒到Swish的最小值，如果使用統一的偏移就會導致精度的下降。而通過學習得到的scale和offset引數可以在量化間隔和啟用值的可表示範圍內有一個較好的權衡，Table6也展示了學習到的offset和固定的offset的結果對比，依舊是通過學習可變的offset精度最高。



Section VI
 Conclusion

本文聚焦於低位元量化的兩大問題：

（1）有符號啟用值的量化問題

（2）量化過程中的訓練穩定性問題

為了解決上述問題，本文提出了一種新的通用的非對稱量化方案，引入可學習的偏移引數，避免引入額外的符號位來完成負數啟用值的量化；此外還採用了新的初始化方案-MSE Initialization提升訓練穩定性。
從而將EfficientNet和MixNet量化至2、3、4bit；此外在ResNet中使用LSQ+量化也不會造成精度損失。