基於內容的影象特徵提取系統
隨著資訊化多媒體時代的到來及世界範圍內Internet的發展,人們在工作和生活中越來越多的接觸到大量的各種各樣的影象資訊。影象作為一種重要的資訊載體,具有直觀、內容豐富、無語言限制和便於國際交流等特點,是組成多媒體資訊的重要內容。影象處理技術已經廣泛深入的應用於各行各業中。
資料庫技術主要研究資料庫的結構、設計以及如何進行資料的組織、儲存、管理。計算機硬體技術的發展和計算機軟體水平的提高,為影象的儲存、壓縮、傳輸、互動提供了必要的基礎。使得影象處理技術和資料庫技術結合成為可能。隨著這一研究領域的發展,影象資料庫成為當今資訊管理的基礎。它既充分利用了影象內部所包含的資訊,又結合了傳統資料庫技術,是一項在理論研究和實際應用中都極有前途的新技術。在浩如煙海的資訊中,尋找感興趣的資料是極其耗時的,人們對資訊檢索和系統的依賴日益加強。傳統的政府辦公系統已經無法適應快速發展的資訊化社會的需求。近年來,多媒體資料庫在政府政務資訊處理中越來越顯示出其快速、便捷的優越效能,受到各國政府的廣泛重視。它不是簡單的辦公自動化、網路化、電子化,而是一個綜合的資訊系統,它是各有關部門和地方各級政府利用資訊和網路通訊技術,是加強政府管理,實現政務公開、提高效率、改進和完善服務職能的重要手段。
1.2 國內外研究現狀
早在70年代,人們就開始了影象檢索技術的研究,實現了基於文字方式的影象檢索。典型框架是:首先對影象進行人工標註,然後應用文字檢索技術實現對標註影象的檢索。這種方法當影象庫中的影象數量不大且影象內容比較單一時,不失為一種簡單易行的方法。然而,當影象資料量非常龐大時,基於文字的影象檢索存在著諸多困難:
首先,手工對影象進行標註所需要的工作量大,效率低;其次,影象內容的複雜多樣使得影象註釋具有較強的主觀性:即使相同的影象,不同的人對影象的理解也不完全一致,存在二義性;另外,對影象而言它不同於文字資訊,影象內容本身不能直接進行排序,不能直接進行準確比較,具有難以用符號描述的視覺特徵資訊,如影象內容的空間關係、影象顏色、紋理、形狀等是難以用準確的詞彙描述的。由於影象內容的豐富內涵以及人們對影象內容進行抽取的主觀性,使得基於文字的方法往往不能準確的檢索,不能取得較為滿意的效果,這種技術的適用範圍及領域受到極大的限制。近年來,一種區別於傳統的基於文字的檢索手段,被稱為基於內容的影象檢索技術成為研究的熱點。
基於內容的影象檢索CBIR(Content Based Image Retrieval),是利用影象內容實現影象檢索的一項綜合性技術,是指根據影象內容特徵以及特徵組合,從影象庫中直接找到含有特定內容的影象。影象的內容特徵包括影象的外觀特徵(顏色、紋理、形狀)和語意。其中,影象的顏色、紋理、形狀等外觀特徵被認為是較低層次上的特徵,具有相對直觀的特點;而語意是較高層次上的特徵,具有相對主觀抽象的特點。事實上,影象的內容特徵是對影象內容的壓縮和抽象,與人類的觀察十分相似,因而基於內容的影象檢索的檢索結果能夠滿足使用者的需要。目前研究和應用的層次主要是採用基於特徵的檢索方式。基於影象內容實現檢索的基本思路是:
首先,通過對影象內容的分析,自動或半自動的提取影象的顏色、紋理、形狀、物件的空間關係等特徵;然後,建立影象的特徵向量作為其索引,利用基於這些特徵定義的相似度量函數計算或評價特徵之間的相似性;
最後,將相似的影象作為檢索結果返回給使用者。在整個的檢索過程中,第一步是至關重要的,它關係到以後的各個環節。因此基於內容的影象特徵提取的研究是一直以來人們關注的焦點,也是本文研究的重點,將在後面做較詳細的分析。
顏色是影象非常重要的視覺特徵,是人識別影象的主要感知特徵之一。相對於其它特徵,顏色特徵對於影象的平移、尺度、旋轉變化不敏感,具有很強的魯棒性,而且計算簡單。基於這些優點,利用顏色特徵進行影象檢索因而受到重視,成為基於內容影象檢索系統中應用最廣泛的主要特徵之一。如何準確充分的提取一幅影象的顏色資訊,並以適當的方式表示,將直接影響整個影象檢索系統的效率和精度。
利用顏色特徵進行影象檢索的關鍵之一是顏色特徵的提取。影象的顏色特徵可以是各種顏色的比例分佈以及顏色空間的分佈等。本章首先介紹了常用的顏色資訊提取和表示方法,其中顏色直方圖的方法是目前效果最好、應用最廣的方法,HSV顏色模型是一種比RGB顏色模型視覺均勻的模型。本文采用了基於HSV顏色空間的顏色直方圖的方法提取影象的顏色特徵。分別獲得影象的色調、亮度以及飽和度資訊,通過加權的方法對影象中的色調、亮度和飽和度進行綜合,使得提取的特徵更接近人對顏色的視覺感知特性,同時演演算法對影象的不同分量根據人類的視覺對顏色感知的經驗值進行非等間隔量化,有效的壓縮了特徵向量的維數,減小了影象特徵資料庫的大小,提高影象的檢索查尋速度。在此基礎上針對含有目標的影象,提出了改進的顏色直方圖的演演算法,即加權顏色直方圖方法。最後對基於這兩種顏色特徵值進行影象檢索的實驗結果進行了比較分析。
在基於內容的影象檢索中,顏色是影象非常重要的視覺特徵。相對於幾何特徵而言,顏色具有一定的穩定性,其對大小、方向都不敏感。因而利用顏色特徵進行影象檢索技術受到重視,並最早得到應用。一般採用直方圖來描述影象的顏色特徵。計算每幅影象的顏色直方圖,即每一種顏色在影象畫素點中的比例,作為影象的特徵向量加以儲存。
1991年,ML Swain和DH Ballard發表了顏色索引一文,使用顏色直方圖求交進行影象顏色相似性計算,邁出了基於內容檢索的第一步。顏色的檢索一般應用於色彩較為豐富的自然圖景的影象檢索中。
3.2 基於顏色的特徵表達
影象的顏色己經是人們注意的記憶影象的主要特徵之一。顏色不像其它資訊那樣揭示物體本質特性,但是顏色作為影象的特徵有其特殊的特點,使得在某些場合下利用顏色進行影象檢索有著很高的效率和準確性。在大自然中,顏色經常標誌了不同的物種。
在人們的生活中,顏色也常常用來作為警示等標誌。顏色作為物體的屬性之一用於影象檢索系統,具有以下特點:
·資料量小。在這個世界上出現的顏色中,只需要採用兩百多種離散的顏色,就可以區分大量的物體。
·顏色特徵與影象位移、尺寸和影象中的物件的位置無關,具有位移不變性、旋轉不變性和尺寸不變性。
·顏色特徵受物體完整性的影響較小。當物體部分的遮擋時,相對於顏色直方圖而言,顏色直方圖受到的影響不是很大。
·顏色直方圖受影象的解析度的影響較小。
·噪聲對檢索效果有一定的影響,但通過某種演演算法很容易減小噪音對匹配工作的影響。
3.3 顏色空間
如何用數值表示紛繁複雜的顏色,人們已經進行了許多研究。研究表明,人眼對顏色的感知是三維的,找到符合人眼視覺特徵的顏色模型是利用顏色特徵進行影象檢索的關鍵。影象的顏色特徵不僅取決於影象本身,而且還與觀察者的視覺系統和觀察經驗有關。因此為了準確提取表徵原始影象顏色資訊,提取演演算法必須在符合人類視覺系統的生理特徵和人類觀察經驗的視覺感知特徵的顏色空間內進行。對彩色影象顏色特徵提取的研究,必須在特定的顏色空間中進行。實際應用中常用到的顏色空間很多,比如L*a*b*顏色空間、RGB空間、HSV空間、Munsell空間、YUV空間等等。
3.3.1 RGB顏色空間
面向硬裝置的最常用顏色模型是RGB模型,它是一種與人的視覺系統結構密切相連的模型。根據人眼結構,所有顏色都可看作是3個基本顏色-紅R,綠G和藍B的不同組合。為了建立標準,國際照度委員會(CIE)早在1931年就規定紅、綠、藍這3種基本色的波長分別為700nm,546.lnm,435.8nm。由於光源的光譜是連續漸變的,所以並沒有一種顏色可準確地叫做紅、綠、藍。因而需要注意,定義3種基本波長並不表明僅由3個固定的R、G、B分量就可組成所有顏色。
RGB模型可以建立在笛卡兒座標系統裡,其中3個軸分別為R,G,B,見圖3-1所示。RGB模型的空間是個正方體,原點對應黑色,離原點最遠的頂點對應白色。在這個模型中,從黑到白灰度值分佈在從原點到最遠頂點間的連線上,而立方體內其餘各點對應不同的顏色,可用從原點到該點的向量表示。一般為方便起見,總將立方體歸一化為單位立方體,這樣所有的R,G,B的值都在區間[0,1]之中。
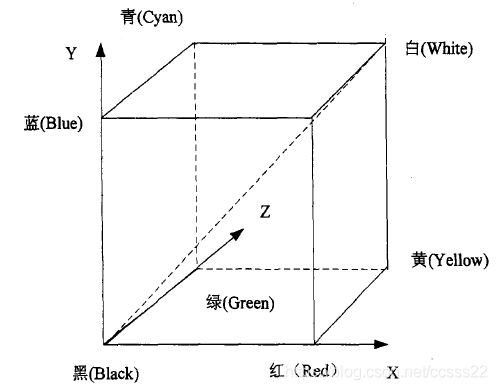
根據這個模型,每幅彩色圖都包括3個獨立的基色平面,或者說可分解到3個平面上。反過來,如果1幅影象可被表示為3個平面,使用這個模型比較方便。色覺的產生需要發光光源的光通過反向或透射方式傳遞到眼睛,刺激視網膜細胞引起神經訊號傳輸到大腦,然後人腦對此加以解釋產生色覺。
3.4.1 顏色特徵的表徵方法
·顏色直方圖法
顏色直方圖是在許多影象檢索系統中被廣泛應用的顏色特徵,具有很好的表現能力。彩色影象的直方圖描述的是不同顏色在整幅影象中所佔的比例,而並不關心每種顏色所處的空間位置。顏色直方圖特別適用於描述那些難以自動分割的影象和不需要考慮物體空間位置的影象。
·顏色矩表示法
顏色矩(Color Moments)特徵是由Stricker和Orengo所提出的。這種方法的數學基礎在於影象中任何的顏色分佈矩可以用它的矩來表示。由於顏色分佈資訊主要集中在低階矩中,因此僅採用顏色的一階矩(mean)、二階矩(variance)、三階矩(skewness)就足以表達影象的顏色分佈。影象的顏色矩一共只需九個分量:三個顏色分量,每個分量上三個低階矩,與其它的顏色特徵相比是非常簡潔的。但是顏色矩特徵的分辨能力較低,一般起到過濾縮小範圍的作用,通常和其它特徵結合使用。
·顏色集表示法
為支援大規模影象庫中的快速查詢,Smith和Chang提出了用顏色集(color set)作為對顏色直方圖的一種近似。首先將影象從RGB空間轉化成視覺均衡的顏色空間中的影象,並將顏色空間量化成若干個bin。然後用色彩自動分割技術將影象分為若干區域,每個區域用量化顏色空間的某個顏色分量來索引,從而將影象表達為一個二進位制的顏色索引集。在影象匹配中,比較不同影象顏色集之間的距離和色彩區域的空間關係。因為顏色集表達為二進位制的特徵向量,可以構造二分查詢數來加快速度,這對於大規模的影象庫十分有利。但在強調了檢索速度的同時,也喪失了查詢的準確性。
·顏色對錶示法
顏色直方圖丟失了顏色的位置資訊,因此它對影象的細緻查詢或對影象中物件的查詢不太合適。如果能夠藉助影象子塊之間顏色的鄰接關係,通過顏色進行組對建模,則若兩幅影象具有相同顏色組對,那麼就建立了這兩幅影象的相似性描述,不僅是在全域性的顏色構成上,而且在區域性位置上的顏色構成上。這就是所謂的顏色對方法。
3.4.2 顏色特徵提取演演算法和MATLAB模擬
本文我們主要研究基於HSV的顏色特徵提取演演算法。本文的影象處理我們採用一下的圖片進行處理:




圖3-4 系統初始處理的影象
HSV顏色空間的每個分量直接對視覺感受起作用,是均勻的顏色空間。HSV模型對應於畫家配比模型,它能較好反映人對顏色的感知和鑑別能力,非常適用用於基於顏色的影象相似比較。從人的心理感知來說,HSV顏色空間要比RGB顏色空間更直觀,更容易接受。
·MATLAB程式設計與模擬
通過上面的分析,我們可以編寫如下的程式碼,首先H,S,V的計算公式的MATLAB程式碼如下所示:
H計算公式:
for i = 1:M
for j = 1:N
%第1級
if h(i,j)>345&&h(i,j)<=360||h(i,j)<=15
H(i,j)=0;
end
%第2級
if h(i,j)>15&&h(i,j)<=25
H(i,j)=1;
end
%第3級
if h(i,j)>25&&h(i,j)<=45
H(i,j)=2;
end
%第4級
if h(i,j)>45&&h(i,j)<=55
H(i,j)=3;
end
%第5級
if h(i,j)>55&&h(i,j)<=80
H(i,j)=4;
end
%第6級
if h(i,j)>80&&h(i,j)<=108
H(i,j)=5;
end
%第7級
if h(i,j)>108&&h(i,j)<=140
H(i,j)=6;
end
%第8級
if h(i,j)>140&&h(i,j)<=165
H(i,j)=7;
end
%第9級
if h(i,j)>165&&h(i,j)<=190
H(i,j)=8;
end
%第10級
if h(i,j)>190&&h(i,j)<=220
H(i,j)=9;
end
%第11級
if h(i,j)>220&&h(i,j)<=255
H(i,j)=10;
end
%第12級
if h(i,j)>255&&h(i,j)<=275
H(i,j)=11;
end
%第13級
if h(i,j)>275&&h(i,j)<=290
H(i,j)=12;
end
%第14級
if h(i,j)>290&&h(i,j)<=316
H(i,j)=13;
end
%第15級
if h(i,j)>316&&h(i,j)<=330
H(i,j)=14;
end
%第16級
if h(i,j)>330&&h(i,j)<=345
H(i,j)=15;
end
end
end
S計算公式:
for i=1:M
for j=1:N
%第1級
if s(i,j)>0&&s(i,j)<=0.15
S(i,j)=0;
end
%第2級
if s(i,j)>0.15&&s(i,j)<=0.4
S(i,j)=1;
end
%第3級
if s(i,j)>0.4&&s(i,j)<=0.75
S(i,j)=2;
end
%第4級
if s(i,j)>0.75&&s(i,j)<=1
S(i,j)=3;
end
end
end
V計算公式:
for i=1:M
for j=1:N
%第1級
if v(i,j)>0&&v(i,j)<=0.15
V(i,j)=0;
end
%第2級
if v(i,j)>0.15&&v(i,j)<=0.4
V(i,j)=1;
end
%第3級
if v(i,j)>0.4&&v(i,j)<=0.75
V(i,j)=2;
end
%第4級
if v(i,j)>0.75&&v(i,j)<=1
V(i,j)=3;
end
end
end
L計算公式:
for i=1:M
for j=1:N
if s(i,j)>0.2&&s(i,j)<=1&&v(i,j)>0.2&&v(i,j)<=1
L(i,j)=16*H(i,j)+4*S(i,j)+V(i,j);
end
end
end
其模擬結果如下所示:

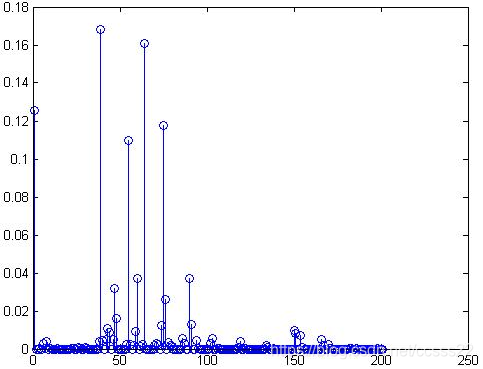
圖3-5 原始圖1的顏色提取效果圖

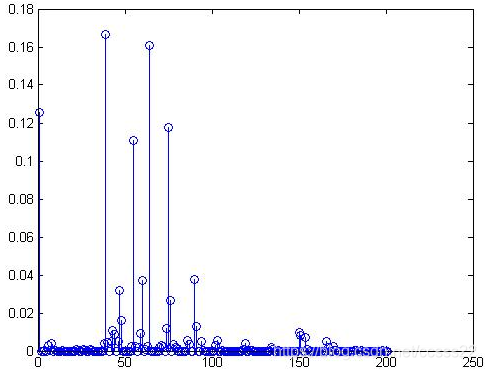
圖3-6 原始圖2的顏色提取效果圖
圖3-5是影象1的HSV空間的L聯合特徵向量直方圖;圖3-6是將原影象旋轉了180度得到彩色影象2以後求得的其L聯合特徵向量直方圖,結果與彩色影象1的完全一致,從而驗證了HSV空間的L特徵向量直方圖同樣具有旋轉不變性。

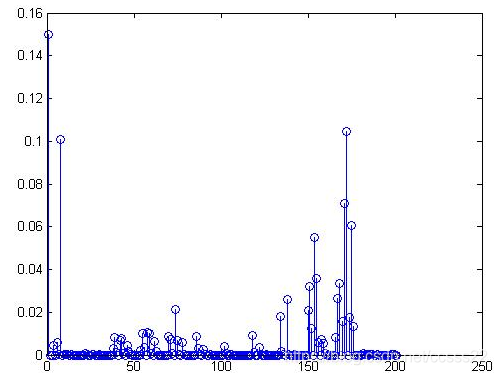
圖3-7 原始圖3的顏色提取效果圖
這個說明不同的影象的顏色提取效果是不同的,通過這個模擬結果我們可以區分不同影象。同樣道理,對於原始圖4其是圖3的旋轉圖,其HSV顏色提取模擬效果和圖3-7是也是完全相同的。
4.1紋理特徵簡介
紋理作為物體的一個重要而又難以描述的特徵,也是基於內容檢索的一條重要線索。基於紋理的特徵提取在區分有相似顏色區域時是非常有用的。各種各樣的技術已經被用來計算紋理的相似性,常用的紋理分析方法是統計方法,如基於共生矩陣的紋理分析,基於馬爾可夫隨機場的紋理分析,基於小波變換的紋理分析方法等。由於紋理分析方法千差萬別,因此對不同的應用領域設計不同的紋理分析方法。
數位影像中的紋理是相鄰畫素的灰度或顏色的空間相關性,或是影象灰度和顏色隨空間位置變化的視覺表現,使用數學或資訊理論的方法抽取的紋理度量稱為紋理特徵。由於紋理特徵可用來對影象中的空間資訊進行一定程度的定量描述,因此也是基於內容的影象檢索中一個重要手段。
4.2 紋理特徵的表徵方法
統計法紋理描述方法利用適合於統計圖形識別的形式來描述紋理。在每個紋理描述結果中,每個紋理屬性用一個特徵向量來描述,它代表了多維特徵空間中的一個點。它的目標是尋找一個確定型的或者概率型的決策規則給紋理賦予特定的類別。統計法紋理描述主要有共生矩陣,分形理論,國際標準MPEG-7提供的邊緣直方圖紋理描述符,數學形態學的方法以及基於自相關函數的紋理描述方法等。
·結構分析方法
結構分析方法的基本思想是認為複雜的紋理可由一些簡單的紋理基元以一定的有規律的形式重複排列組合而成。如果定義出一些排列基元的規則,就有可能將某些紋理基元按照規定的方式組織成所需要的紋理模式。紋理基元描述了區域性紋理特徵,對整幅影象中不同紋理基元的分佈統計可獲得影象的全面紋理資訊。對於存在於紋理基元之間的結構關係,可以有不同的分析途徑。最簡單的方法是分析紋理基元之間存在相位、距離、尺寸等統計特徵,也可以考慮用複雜的方法分析,如利用模型或句法等。
·統計分析方法
該方法利用紋理的統計特性和規律來描述紋理,它適用於像木紋、砂地、草坪那樣的細而不規則的自然紋理,也同樣適用於人工紋理,是最早應用在紋理分析中的方法之一。統計方法從根據畫素灰度值的統計分析出發,推匯出一些統計量表達紋理特徵。根據特徵計算時所使用的點的個數,此類方法又可分為一階統計量、二階統計量和高階統計量。
在本章,我們將要模擬的原始影象如下所示:


圖4-1 原始影象
我們首先利用顏色提取的方法對影象進行模擬,得到如下的模擬結果:
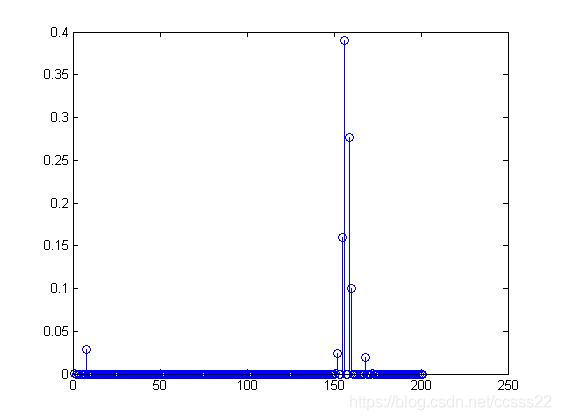
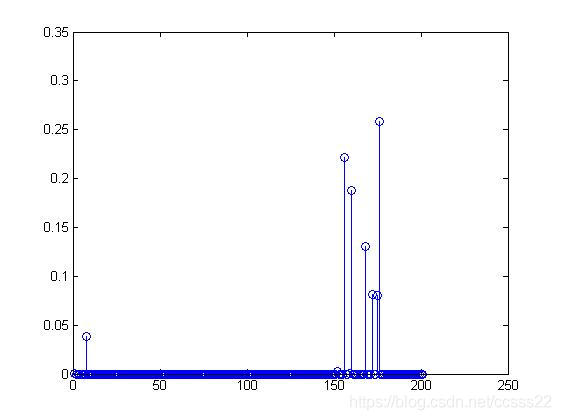
圖4-2 顏色提取模擬圖
通過模擬我們發現當兩個顏色大致相同的時候(這裡都為藍色為主色調),那麼通過顏色提取後其結果相似,上圖中其峰值都在150左右開始,如果我們要識別的影象顏色更接近,那麼其峰值機會相同,這對我們影象的檢索造成困難,所以這裡我們將對這類圖片進行進一步的測試,我們將根據其紋理進行判斷。
那麼在這種情況下,我們就需要對其紋理進行提取,即在模擬中對於同一點的幅度進行比較,其程式碼較長,這裡我們直接給出模擬結果圖:

圖4-3 圖一的紋理提取模擬結果
我們可以看到其峰值的最值為2多點。
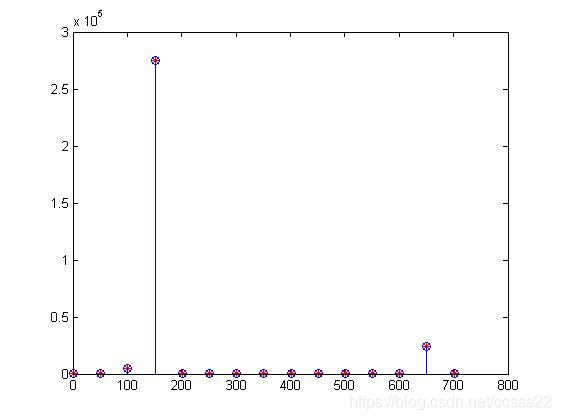
圖4-4 圖二的紋理提取模擬結果
我們可以看到其峰值的最值為2.5多點。
通過對比就能分析出是不同的圖片。
1-顏色特徵提取
clc;
clear;
close all;
Image=imread('2.bmp');
[M,N,O]=size(Image);
[h,s,v]=rgb2hsv(Image);
H=h;
S=s;
V=v;
h=h*360;
for i=1:M
for j=1:N
if v(i,j)<0.2
L(i,j)=0;
end
if s(i,j)<0.2&&v(i,j)>0.2&&v(i,j)<=0.8
L(i,j)=(v(i,j)-0.2)*10+1;
end
if s(i,j)<0.2&&v(i,j)>0.8&&v(i,j)<=1
L(i,j)=7;
end
end
end
%*************************************************
% h量化成16級;
% s量化成4級;
% v量化成4級;
for i = 1:M
for j = 1:N
%第1級
if h(i,j)>345&&h(i,j)<=360||h(i,j)<=15
H(i,j)=0;
end
%第2級
if h(i,j)>15&&h(i,j)<=25
H(i,j)=1;
end
%第3級
if h(i,j)>25&&h(i,j)<=45
H(i,j)=2;
end
%第4級
if h(i,j)>45&&h(i,j)<=55
H(i,j)=3;
end
%第5級
if h(i,j)>55&&h(i,j)<=80
H(i,j)=4;
end
%第6級
if h(i,j)>80&&h(i,j)<=108
H(i,j)=5;
end
%第7級
if h(i,j)>108&&h(i,j)<=140
H(i,j)=6;
end
%第8級
if h(i,j)>140&&h(i,j)<=165
H(i,j)=7;
end
%第9級
if h(i,j)>165&&h(i,j)<=190
H(i,j)=8;
end
%第10級
if h(i,j)>190&&h(i,j)<=220
H(i,j)=9;
end
%第11級
if h(i,j)>220&&h(i,j)<=255
H(i,j)=10;
end
%第12級
if h(i,j)>255&&h(i,j)<=275
H(i,j)=11;
end
%第13級
if h(i,j)>275&&h(i,j)<=290
H(i,j)=12;
end
%第14級
if h(i,j)>290&&h(i,j)<=316
H(i,j)=13;
end
%第15級
if h(i,j)>316&&h(i,j)<=330
H(i,j)=14;
end
%第16級
if h(i,j)>330&&h(i,j)<=345
H(i,j)=15;
end
end
end
for i=1:M
for j=1:N
%第1級
if s(i,j)>0&&s(i,j)<=0.15
S(i,j)=0;
end
%第2級
if s(i,j)>0.15&&s(i,j)<=0.4
S(i,j)=1;
end
%第3級
if s(i,j)>0.4&&s(i,j)<=0.75
S(i,j)=2;
end
%第4級
if s(i,j)>0.75&&s(i,j)<=1
S(i,j)=3;
end
end
end
for i=1:M
for j=1:N
%第1級
if v(i,j)>0&&v(i,j)<=0.15
V(i,j)=0;
end
%第2級
if v(i,j)>0.15&&v(i,j)<=0.4
V(i,j)=1;
end
%第3級
if v(i,j)>0.4&&v(i,j)<=0.75
V(i,j)=2;
end
%第4級
if v(i,j)>0.75&&v(i,j)<=1
V(i,j)=3;
end
end
end
%將三個顏色分量合成為一維特徵向量
for i=1:M
for j=1:N
if s(i,j)>0.2&&s(i,j)<=1&&v(i,j)>0.2&&v(i,j)<=1
L(i,j)=16*H(i,j)+4*S(i,j)+V(i,j);
end
end
end
%計算L的直方圖
for i=0:200
Hist(i+1)=size(find(L==i),1);
end
Hist = Hist/sum(Hist)
i=0:1:200
figure,stem(i+1,Hist(i+1));
2-紋理提取
clc;
clear;
close all
IN=imread('2.bmp');
gray=256;
[R,C]=size(IN);
%採用平方求和計算梯度矩陣
GM=zeros(R-1,C-1);
for i=1:R-1
for j=1:C-1
n_GM=(IN(i,j+1)-IN(i,j))^2+(IN(i+1,j)-IN(i,j))^2;
GM(i,j)=sqrt(double(n_GM));
end
end
% figure,imshow(GM);
%找出最大值最小值
n_min=min(GM(:));
n_max=max(GM(:));
%把梯度圖象灰度級離散化
new_gray=32;
%新的梯度矩陣為new_GM
new_GM=zeros(R-1,C-1);
new_GM=uint8((GM-n_min)/(n_max-n_min)*(new_gray-1));
%計算灰度梯度共生矩陣
%梯度矩陣比軌度矩陣維數少1,忽略灰度矩陣最外圍
H=zeros(gray,new_gray);
for i=1:R-1
for j=1:C-1
H(IN(i,j)+1,new_GM(i,j)+1)= H(IN(i,j)+1,new_GM(i,j)+1)+1;
end
end
%歸一化灰度梯度矩陣 H_basic
total=i*j;
H_basic=H/total;
%小梯度優勢 T1
TT=sum(H);
T1=0;
for j=1:new_gray
T1=T1+TT(1,j)/j^2;
end
T1=T1/total;
%計算大梯度優勢 T2
T2=0;
for j=1:new_gray
T2=T2+TT(1,j)*(j-1);
end
T2=T2/total;
%計算灰度分佈的不均勻性 T3
T3=0;
TT1=sum(H');
for j=1:gray
T3=T3+TT1(1,j)^2;
end
T3=T3/total;
%計算梯度分佈的不均勻性 T4
T4=0;
for j=1:new_gray
T4=T4+TT(1,j)^2;
end
T4=T4/total;
%計算能量 T5
T5=0;
for i=1:gray
for j=1:new_gray
T5=T5+H_basic(i,j)^2;
end
end
%計算灰度平均 T6
TT2=sum((H_basic)');
T6=0;
for j=1:gray
T6=T6+(j-1)*TT2(1,j);
end
%計算梯度平均 T7
T7=0;
TT3=sum(H_basic);
for j=1:new_gray
T7=T7+(j-1)*TT3(1,j);
end
%計算灰度均方差 T8
T8=0;
for j=1:gray
T8=T8+(j-1-T6)^2*TT2(1,j);
end
T8=sqrt(T8);
%計算梯度均方差 T9
T9=0;
for j=1:new_gray
T9=T9+(j-1-T7)^2*TT3(1,j);
end
T9=sqrt(T9);
% 計算相關 T10
T10=0;
for i=1:gray
for j=1:new_gray
T10=T10+(i-1-T6)*(j-1-T7)*H_basic(i,j);
end
end
%計算灰度熵 T11
T11=0;
for j=1:gray
T11=T11+TT2(1,j)*log10(TT2(1,j)+eps);
end
T11=-T11;
%計算梯度熵 T12
T12=0;
for j=1:new_gray
T12=T12+TT3(1,j)*log10(TT3(1,j)+eps);
end
T12=-T12;
%計算混合熵 T13
T13=0;
for i=1:gray
for j=1:new_gray
T13=T13+H_basic(i,j)*log10(H_basic(i,j)+eps);
end
end
T13=-T13;
%計算慣性 T14
T14=0;
for i=1:gray
for j=1:new_gray
T14=T14+(i-j)^2*H_basic(i,j);
end
end
%計算逆差矩 T15
T15=0;
for i=1:gray
for j=1:new_gray
T15=T15+H_basic(i,j)/(1+(i-j)^2);
end
end
x=1:50:750;
OUT(1,1)=T1;
OUT(1,2)=T2;
OUT(1,3)=T3;
OUT(1,4)=T4;
OUT(1,5)=T5;
OUT(1,6)=T6;
OUT(1,7)=T7;
OUT(1,8)=T8;
OUT(1,9)=T9;
OUT(1,10)=T10;
OUT(1,11)=T11;
OUT(1,12)=T12;
OUT(1,13)=T13;
OUT(1,14)=T14;
OUT(1,15)=T15;
for num=1:15
if num>2
stem(x,OUT,'-');
hold on;
else
stem(x,OUT,'-*r');
hold on;
end
end