基於FPGA的混沌訊號發生器設計與實現

提出基於FPGA設計混沌訊號發生器的一種改進方法。首先，採用Euler演演算法，將連續混沌系統轉換為離散混沌系統。其次，基於IEEE-754單精度浮點數標準和模組化設計理念，利用Quartus II軟體，採用VHDL和原理圖相結合的方式設計混沌訊號發生器。最後，在FPGA實驗系統上進行實驗，在示波器上顯示了混沌吸引子的相圖及時域混沌訊號。由於採用了基於資料選擇器的面積優化方法，複用耗費邏輯資源較多的浮點運算模組，大大減少了混沌訊號發生器所佔用的FPGA邏輯資源。實驗結果證明了該方法的有效性和通用性。

0 引言

用分立元件的類比電子電路產生混沌訊號是目前最常用的方法[1,2]，但元器件容易老化，系統改變不靈活，因此人們考慮能否使用數位器件（如FPGA）代替模擬元件完成相應的功能，以提高混沌保密通訊系統設計的靈活性、系統的安全性和實用性。Aseeri, M.A.等人[3]提出用FPGA技術實現Lorenz混沌系統的方法。張鈺等人[4]提出用FPGA技術產生多渦卷超混沌吸引子的新方法。王忠林等人[5]提出了一種基於FPGA 平臺和EDA 開發工具實現混沌吸引子的方法。文獻[3,4,5]所採用的均是DSP Builder技術，而不是根據IEEE-754標準用硬體描述語言來實現的，其主要缺點是不能從根本上解決時序控制等問題，在混沌同步及其在保密通訊中的應用受到了限制。周武傑等人[6]提出了基於IEEE-754標準的現場可程式化門陣列(FPGA)通用混沌與超混沌訊號產生器設計與硬體實現的一種新方法。該方法具有通用性強的優點，並且從根本上解決了時序控制問題。但該方法中，浮點運算器模組的程式設計難度較高而且混沌系統佔用FPGA邏輯資源較多。本文在文獻[6]的基礎上做了兩點改進：（1）利用QuartusⅡ提供的浮點乘法器和加/減法器的兆功能函數，自客製化出滿足設計要求的浮點運算器模組，無需程式設計，減低了設計難度，提高了設計效率。（2）採用了基於資料選擇器的面積優化方法，複用耗費邏輯資源較多的浮點運算模組，基於Altera EP1C3T144C8晶片（僅含有2910個邏輯單元）成功設計並實現了Lorenz、Chen、蔡氏混沌訊號發生器。方便起見，本文以Lorenz混沌訊號發生器設計和實現為例進行說明。

IEEE-754單精度浮點數格式[7]為32位元，如圖1所示。

31	30               23	22            0
S	E	F

圖1 單精度浮點數格式

其中，第31位元是符號位（S），第30至23位是8位元的階碼（E），第22至0位是23位的尾數（F），偏移值為127，尾數有一位隱藏位。對於規格化數，0<E<255，值V=(-1)S×2E-127×1.F。

(3)式中常數的十進位制格式與IEEE-754單精度格式之間的對應關係如表1所列。

表1系統引數的十進位制格式與單精度格式的對應關係

十進位制	單精度	十進位制	單精度
0.99	3F7D70A3	0.999	3F7FBE76
0.01	3C23D70A	0.001	3A83126E
0.028	3CE56041	0.9973333	3F7F513C

 

根據(3)式，用FPGA技術設計Lorenz混沌系統的主要設計理念在於將整個系統劃分為若干個基本功能模組，主要包括浮點乘法器、浮點加/減法器、資料選擇器、資料分配器、時序控制模組和數值轉換模組等主要模組。現對其作簡要分析。

3.1 浮點乘法器和浮點加/減法器

由(3)式可知，欲實現Lorenz混沌系統，離不開浮點乘法器和浮點加/減法器。利用QuartusⅡ提供的浮點乘法器和加/減法器的兆功能函數，可自客製化出滿足設計要求的浮點運算器模組，無需程式設計，簡單易行，減低了設計難度，提高了設計效率。

浮點乘法器和浮點加/減法器被存放在QuartusⅡ軟體的安裝目錄下的altera/72/quartus/libraries/megafunctions/arithmetic資料夾中，其名稱分別是altfp_mult和altfp_add_sub。使用者可通過MegaWizard嚮導，生成實際可用的電路模組，並定義好該兆功能函數的各項引數。本設計中，浮點乘法器和浮點加/減法器均採用IEEE-754的32位元單精度浮點數格式，輸出反應時間均為10個clk週期，分別佔用1399和697個邏輯單元。

3.2 資料選擇器

由(3)式可知，進行一次完整的迭代計算，需做8次浮點乘法運算（因為0.001x(n-1)只需計算一次）以及4次浮點加法或減法運算。此外，因為Lorenz混沌系統的變數x∈(-20,20)，需將其加上某個常數（如20）變為非負數，以便於單極性DA轉換器輸出模擬訊號，所以還需做一次加法運算。顯然，若不經優化，僅浮點運算器將佔用1399×8+697×5=14677個邏輯單元。

為減少了FPGA晶片邏輯資源的使用量，同時也降低晶片的功耗，本設計採用了基於資料選擇器的面積優化方法。其主要思想是利用速度的優勢換取面積的節約，在系統工作頻率允許的情況下，針對資料通路中耗費邏輯資源比較多的模組，通過多路選擇的方法進行復用，以減少該模組的使用個數，達到減少資源使用，優化面積的目的。

本設計正是基於上述面積優化思想，採用了4個32位元8選1資料選擇器來複用浮點乘法器和浮點加/減法器各一個，最終基於Altera EP1C3T144C8晶片（僅含2910個邏輯單元）成功實現了Lorenz混沌系統。

3.3 資料分配器

資料分配器與資料選擇器的功能正好相反，它用於對浮點乘法、浮點加/減法運算結果進行分配，使其分配到相應的資料暫存器進行寄存。雖然QuartusⅡ軟體沒有現成的資料分配器模組，但是可以通過VHDL程式設計自行設計實現。

3.4 時序控制模組

時序控制模組為浮點乘法器、浮點加/減法器、資料選擇器、資料分配器等模組提供時序控制訊號，以協調各模組有序工作。

時序控制模組採用有限狀態機程式設計實現，由13個狀態組成，為保證有足夠的時間完成浮點運算，每個狀態保持時間為11個clk週期。程式設計時，最好採用將狀態暫存器、次態邏輯和輸出邏輯在一個程序裡描述的單程序狀態機，這樣輸出訊號被鎖存後由時序器件同步輸出，能夠很好地改善毛刺現象。

時序控制模組的時序模擬結果如圖2所示。

 

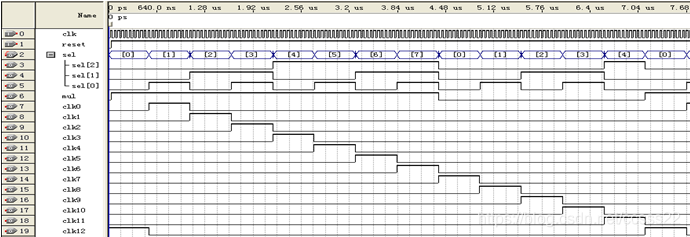
圖2 時序控制模組的時序模擬結果

圖2中， clk為時鐘輸入訊號，reset為復位輸入訊號，其餘為輸出訊號，其中sel為資料選擇器和資料分配器的選擇訊號，mul為浮點乘法器使能訊號，clk0~clk12為13個32位元資料暫存器的時鐘訊號。由圖可見，輸出訊號沒有出現任何毛刺。

3.5數值轉換模組

FPGA僅能輸出數位訊號，必須外接數模轉換器才能實現數位訊號到模擬訊號的轉換。本設計中使用的是10位的DA轉換器THS5651。數值轉換模組用於將32位元單精度浮點數轉換成10位的數位量，只有這樣FPGA才可以和THS5651相連。

(3)式所描述的Lorenz混沌系統的狀態變數x∈(-20,20)，z∈(0,50)。為便於單極性DA轉換器輸出模擬訊號，需將Lorenz混沌系統的狀態變數x加上20，記為x’，則x’，z∈(0,50)，其32位元單精度浮點格式的階碼最大值應為10000100。

數值轉換模組採用VHDL程式設計實現，其輸入datain（31downto 0）與輸出資料dataout（9 downto 0）的對應關係如表2所示。

表2 32位元浮點數與10位數位量的對應關係

datain(30 downto 23)	dataout(9 downto 0)
"10000100"	"1" & datain(22 downto 14)
"10000011"	"01" & datain(22 downto 15)
"10000010"	"001" & datain(22 downto 16)
"10000001"	"0001" & datain(22 downto 17)
"10000000"	"00001" & datain(22 downto 18)
"01111111"	"000001" & datain(22 downto 19)
"01111110"	"0000001" & datain(22 downto 20)
"01111101"	"00000001" & datain(22 downto 21)
"01111100"	"000000001" & datain(22)
"01111011"	"0000000001"
others	"0000000000"