考研複習:有關連續的定理、間斷點及其分類
連續
初等函數的連續性
一 切 基 本 初 等 函 數 都 是 其 定 義 域 上 的 連 續 函 數 一切基本初等函數都是其\pmb{定義域}上的連續函數 一切基本初等函數都是其定義域定義域定義域上的連續函數
↓ ↓ ↓
( 任 何 初 等 函 數 都 是 經 有 限 次 四 則 運 算 和 復 合 運 算 得 到 的 ) (任何初等函數都是經有限次四則運算和複合運算得到的) (任何初等函數都是經有限次四則運算和復合運算得到的)
↓ ↓ ↓
所 以 , 任 何 初 等 函 數 都 是 其 定 義 區 間 上 的 連 續 函 數 所以,任何初等函數都是其\pmb{定義區間}上的連續函數 所以,任何初等函數都是其定義區間定義區間定義區間上的連續函數
最大值與最小值定理
f
f
f是定義在數集D上的函數,若存在任意
x
0
∈
D
x_0∈D
x0∈D,對一切
x
∈
D
x∈D
x∈D,有
f
(
x
0
)
≥
f
(
x
)
f(x_0)≥f(x)
f(x0)≥f(x)
則稱
f
f
f在D上有最大值。(最小值同理)
介值性定理
設函數
f
f
f在閉區間[a,b]上連續,
f
(
a
)
≠
f
(
b
)
f(a)≠f(b)
f(a)=f(b),有下圖存在
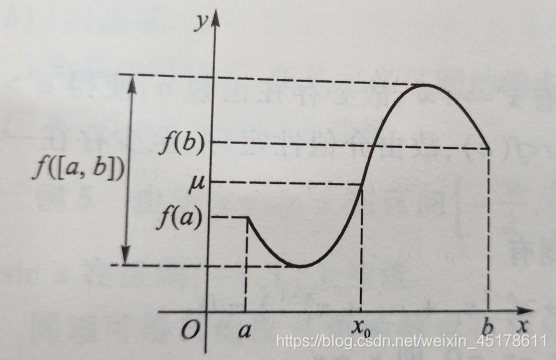
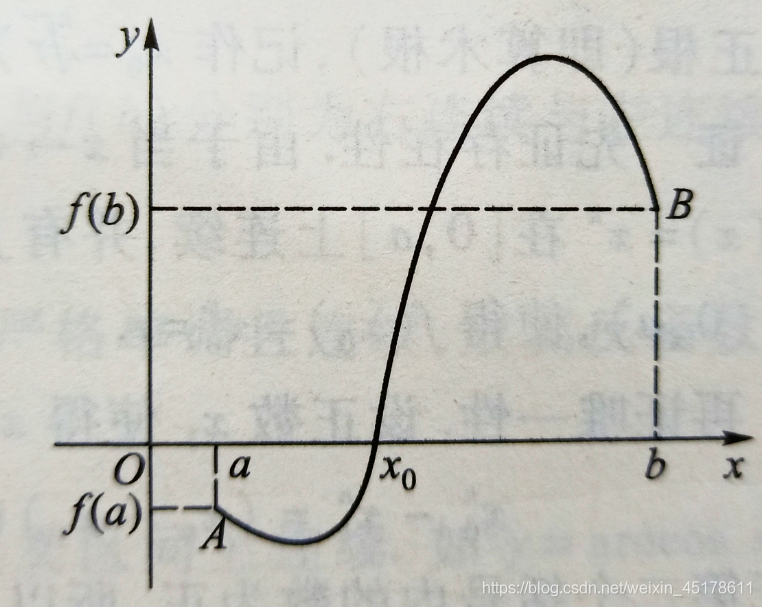
推論:根的存在性定理
設函數
f
f
f在閉區間[a,b]上連續,
f
(
a
)
f(a)
f(a)與
f
(
b
)
f(b)
f(b)異號,即(
f
(
a
)
f
(
b
)
<
0
f(a)f(b)<0
f(a)f(b)<0),則至少存在一點
x
0
∈
(
a
,
b
)
x_0∈(a,b)
x0∈(a,b),使得
f
(
x
)
=
0
f(x)=0
f(x)=0
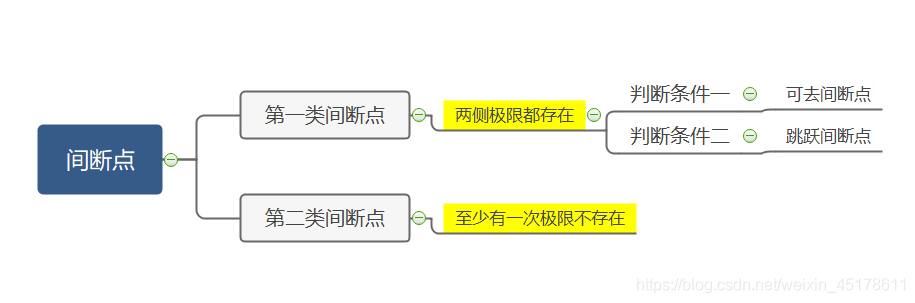
間斷點及其分類
如果函數 f f f有定義,若 f f f在 x 0 x_0 x0處無定義或有定義但不連續,則稱 x 0 x_0 x0為函數 f f f的間斷點或不連續點。
如果 x 0 x_0 x0為 f f f的間斷點,則必會出現下列情形之一:
(條件一) f f f在 x 0 x_0 x0無定義,或極限 lim x → x 0 f ( x ) \lim\limits_{x\rightarrow\ x_0}f(x) x→ x0limf(x)不存在
(條件二) f f f在 x 0 x_0 x0有定義,且極限 lim x → x 0 f ( x ) \lim\limits_{x\rightarrow\ x_0}f(x) x→ x0limf(x)存在,但 lim x → x 0 f ( x ) ≠ f ( x 0 ) \lim\limits_{x\rightarrow\ x_0}f(x)≠f(x_0) x→ x0limf(x)=f(x0)
根據間斷點的型別可以分為下面型別: