P1002 過河卒（dp法）

P1002 過河卒

題目描述

棋盤上 AA 點有一個過河卒，需要走到目標 BB 點。卒行走的規則：可以向下、或者向右。同時在棋盤上 CC 點有一個對方的馬，該馬所在的點和所有跳躍一步可達的點稱為對方馬的控制點。因此稱之為「馬攔過河卒」。

棋盤用座標表示，AA 點 (0, 0)(0,0)、BB 點 (n, m)(n,m)，同樣馬的位置座標是需要給出的。

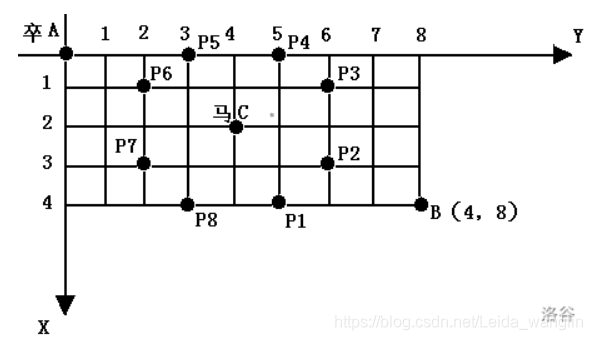
現在要求你計算出卒從 AA 點能夠到達 BB 點的路徑的條數，假設馬的位置是固定不動的，並不是卒走一步馬走一步。

輸入格式

一行四個正整數，分別表示 BB 點座標和馬的座標。

輸出格式

一個整數，表示所有的路徑條數。

輸入輸出樣例

輸入 #1

6 6 3 3

輸出 #1

6

說明/提示

對於 100% 的資料，1 <= n, m <= 20，0≤ 馬的座標 ≤ 20。

我的思路

核心想法：每個點的路徑條數是該點左邊路徑條數加上上邊路徑條數

dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; 

要注意的是：陣列的邊界，給馬的控制點做標記時，要考慮邊界

if (bx >= 0 && bx <= 20 && by >= 0 && by <= 20)
      bj[bx][by] = -1;

當計算i – 0 時，只需加上他上邊的路徑條數，相同，j == 0，只需加上左邊的路徑條數。

   continue;
      if (i == 0)
        dp[i][j] = dp[i][j - 1];
      else if (j == 0)
        dp[i][j] = dp[i - 1][j];

我的程式碼

#include<bits/stdc++.h>
using namespace std;
int n, m, x, y, bx, by;
long long bj[30][30], dp[30][30], z[8][2] = {{1, -2}, {-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}}; 
int main() {
  cin >> n >> m >> x >> y;
  for (int i = 0; i < 8; i++) {
    bx = x + z[i][0];
    by = y + z[i][1];
    if (bx >= 0 && bx <= 20 && by >= 0 && by <= 20)
      bj[bx][by] = -1;
  } 
  bj[x][y] = -1;
  dp[0][0] = 1;
  for (int i = 0; i <= n; i++) {
    for (int j = 0; j <= m; j++) {
      if (bj[i][j] == -1 || (i == 0 && j == 0))
        continue;
      if (i == 0)
        dp[i][j] = dp[i][j - 1];
      else if (j == 0)
        dp[i][j] = dp[i - 1][j];
      else
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  
    }  
  }
  cout << dp[n][m];
  return 0;
}