25行程式碼AC_ 2017年C/C++ A組第四題 方格分割（dfs剪痕+解題報告）

勵志用少的程式碼做高效表達

---

問題描述：

6x6的方格，沿著格子的邊線剪開成兩部分。
要求這兩部分的形狀完全相同。
 
如圖：p1.png, p2.png, p3.png 就是可行的分割法。
 
試計算：
包括這3種分法在內，一共有多少種不同的分割方法。
注意：旋轉對稱的屬於同一種分割法。

---

題意分析

幾種分析思路：

暴力列舉： 直接列舉18個點，然後判斷。 但時間耗費太高。 放棄。

對格子dfs：dfs無法識別T型圖案(因為深搜只能遍歷一條路)，因此放棄

想了又想， 如果對邊線進行dfs，從中間點出發，最後只要用深搜能到達邊界， 就代表著這條線把整個圖案分成了兩半。 思路就出來了！

剪刀剪痕與dfs邊界如下圖所示：

---

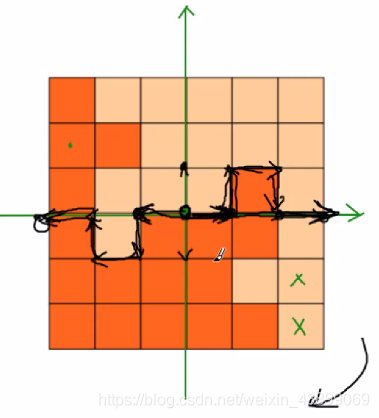
程式碼展示：

#include<iostream>
using namespace std;
int vis[10][10];
int dire[4][2] = {-1,0, 1,0, 0,-1, 0,1};
int ans;

void dfs(int x, int y) {
	if(x==0 || y==6 || x==6 || y==0) {
		ans++; return;
	}
//	當前的點標註為已存取
	vis[x][y] = 1;
	vis[6-x][6-y] = 1; 
	for(int i = 0; i < 4; i++) {
		int tx = x+dire[i][0];
		int ty = y+dire[i][1];
//		新座標
		if(tx<0 || tx>6 || ty<0 || ty>6) continue;
		if(!vis[tx][ty]) dfs(tx, ty); 
	}
	vis[x][y] = 0;
	vis[6-x][6-y] = 0;
}

int main() {
	vis[3][3] = 1;
	dfs(3, 3);
	cout << ans/4 << endl;
return 0; } 

---

感想與總結

1、藍橋杯的絕大多數題都是搜尋或暴力，而近兩年純暴力的題越來越少，取而代之的是模擬+搜尋或暴力+搜尋。

2、本題就是一道非常標準的 模擬+搜尋 型別題。 關於暴力+搜尋，可參考2016年B組7題的剪郵票， 也很經典， 題目+題解，傳送門

3、對於對稱型別的題， 一定要考慮是否有重複的情況出現。

---

每日一句

把手舉過頭頂，突然張開五指，那麼，恭喜你給自己放了個煙花！