BP推導全過程

最近老師佈置了一個神經網路的作業，正好練習下LaTeX，順便寫了這個部落格
BP的整個過程還是很嚴謹的、LaTeX寫公式也很好用，建議一步步跟著公式走
另外還配上了程式碼供食用，程式碼配公式、效果更好

一些變數的含義

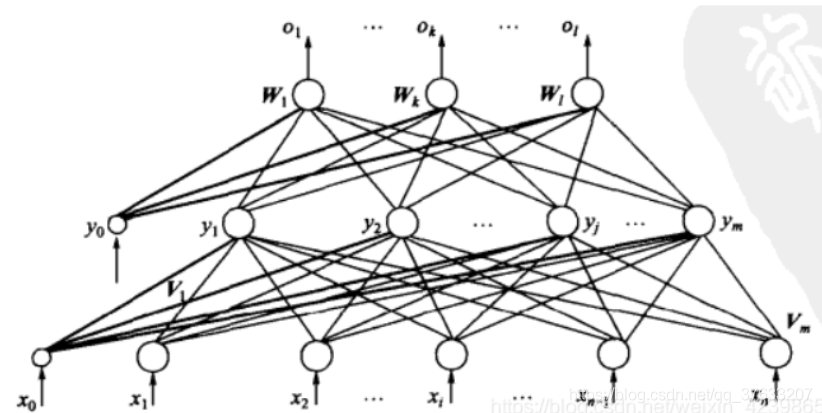
這裡的的網路採用三層感知機結構
在這裡插入圖片描述

以簡單的sigmod函數如為例：
$(x)=\frac {1}{1+e^{-x}}\\ f(x)'=f(x)(1-f(x))$
下面定義一些變數
$輸入向量X=(x_1,x_2,\cdots x_n)^T \\ 隱層輸出向量Y=(y_1,y_2,\cdots y_m)^T\\ 輸入層到隱層的權重V\\ V=(V_1,V_2,\cdots,V_m)\\ 這裡的V_j,j\in (1,\cdots,m)是下面矩陣的列向量\\ 表示式為：f(V_j \cdot X)=Y_j\\ V=\left[ \begin{array}{ccc} v_{11} & v_{12} & \cdots & v_{1m}\\ v_{21} & v_{22} & \cdots & v_{2m}\\ v_{31} & v_{32} & \cdots & v_{3m}\\ \cdots & \cdots&\cdots & \cdots \\ v_{n1} & v_{n2} & \cdots & v_{nm}\\ \end{array} \right]\\ \\ 輸出層向量O=(o_1,o_2,\cdots,o_l)^{T}\\ 真實標籤D=(d_1,d_2,\cdots,d_l)^T\\ 隱含層到輸出層的權重W\\ W=(W_1,W_2,\cdots,W_l)\\ W_k,k\in(1,\cdots,l)為下面矩陣的第k個列向量\\ W=\left[ \begin{array}{ccc} w_{11} & w_{12} & \cdots & w_{1l}\\ w_{21} & w_{22} & \cdots & w_{2l}\\ w_{31} & w_{32} & \cdots & w_{3l}\\ \cdots & \cdots&\cdots & \cdots \\ w_{m1} & w_{n2} & \cdots & w_{ml}\\ \end{array} \right]\\ 下面公式表示的是隱藏層到輸出層的過程 f(W_k\cdot Y)=O_k$

一些公式

對於輸出層有(後面兩個式子不過是展開了內積而已，本質一樣)：
$o_k=f(net_k)=f(\sum_{j=0}^mw_{jk}y_j)=f(W_kY) \quad \quad \quad (1)$
對於隱含層
$y_j=f(net_j)=f(\sum_{i=0}^nv_{ij}x_i)=f(V_jX) \quad \quad \quad (2)$
對於輸出層的梯度更新公式:
$輸出層梯度更新量\quad\quad\Delta w_{jk}=-\eta \frac{\partial E}{\partial w_{jk}} \\ w_{jk}=w_{jk}+\Delta w_{jk}=w_{jk}-\eta\frac{\partial E}{\partial w_{jk}} \quad \quad(3)$
對於隱藏層的更新公式
$隱藏層梯度更新量\quad\quad\Delta v_{ij}=-\eta \frac{\partial E}{\partial v_{ij}} \\ v_{ij}=v_{ij}+\Delta v_{ij}=v_{ij}-\eta\frac{\partial E}{\partial v_{ij}} \quad\quad\quad(4)$
最後的誤差公式的展開如下
$E=\frac{1}{2}\sum_{k=1}^l(d_k-o_k)^2 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\ 把公式（1）（2）帶入\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\ =\frac{1}{2}\sum_{k=1}^l(d_k-f[\sum_{j=0}^m w_{jk}f(net_j)])^2 \quad\quad\quad\quad\quad\quad\\ =\frac{1}{2} \sum_{k=1}^l (d_k-f[\sum_{j=0}^m w_{jk}f(\sum_{i=0}^nv_{ij}x_i)])^2\quad\quad\quad(5)$

開始推導

由上面的公式（3）（4）可知我們只要求出那兩個梯度更新量就行了

對於輸出層的梯度更新量，我們利用鏈式求導可以得到下面的公式
$\Delta w_{jk}=-\eta \frac{\partial E}{\partial w_{jk}}=-\eta\frac{\partial E}{\partial net_k}\frac{\partial net_k}{\partial w_{jk}}\\ 由公式（1）可知 \frac{\partial net_k}{\partial w_{jk}}=y_j\\ 即\Delta w_{jk}=-\eta\frac{\partial E}{\partial net_k}y_j \quad\quad\quad(6)\\$
對於隱藏層的梯度更新量，也是如此
$\Delta v_{ij}=-\eta \frac{\partial E}{\partial v_{ij}}=-\eta\frac{\partial E}{\partial net_j}\frac{\partial net_j}{\partial v_{ij}}\\ 由公式（2）可知 \frac{\partial net_j}{\partial v_{ij}}=x_i\\ 即\Delta v_{ij}=-\eta\frac{\partial E}{\partial net_j}x_i\quad\quad\quad(7)\\ 實際程式碼中我們求x_i 和y_j輕輕鬆鬆，只要儲存網路每層的輸出即可\\ 而且我們都是批次更新，批次更新效率更高$
所以我們只要求出下面兩個公式即可求出對於每一層的梯度更新量
$我們把-\frac{\partial E}{\partial net_k}設為err_o\quad意思為輸出層的誤差訊號\\ 再把-\frac{\partial E}{\partial net_j}設為err_y\quad意思為隱含層層的誤差訊號\\ err_o和err_y展開可得:\\ err_o=-\frac{\partial E}{\partial net_k}=-\frac{\partial E}{\partial o_k}\frac{\partial o_k}{\partial net_k}\\把公式(1)(5)代入上公式可得 \\ err_o=-\frac{\partial E}{\partial o_k}f(net_k)'=\sum_{k=1}^l(d_k-o_k)o_k(1-o_k)\quad\quad(8)\\ 可以看出來輸出層的誤差訊號還是非常好求的\\ err_y稍微複雜點，我們還是先把他展開\\ err_y=-\frac{\partial E}{\partial net_j}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\ =-\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial net_j}\quad\quad\quad\quad\quad\quad\\ =-\frac{\partial E}{\partial o_k}\frac{\partial o_k}{\partial y_j}\frac{\partial y_j}{\partial net_j}\quad\quad\quad\quad\\ =-\frac{\partial E}{\partial o_k}\frac{\partial o_k}{\partial net_k}\frac{\partial net_k}{\partial y_j}\frac{\partial y_j}{\partial net_j}\quad\\ 上面這幾個求偏導的公式都有我們只需要帶入公式(1)(2)(5)可得\\ err_y=\sum_{k=0}^l(d_k-o_k)\cdot o_k(1-o_k)\cdot w_{jk} \cdot y_j(1-y_j)\quad(9)\\ 我們觀察可以發現err_y的一部分和err_o一模一樣，所以把公式(8)帶入(9)\\ 得err_y=err_ow_{jk}y_j(1-y_j)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(10)\\ 對於寫程式碼來說,我們只要求出err_o後，後面一系列的隱藏層都非常好求\\ 只要用從後向前計算每一層的誤差訊號即可\\$
那麼我們最終的結果就是如下公式
$\Delta w_{jk}=\eta\cdot err_o \cdot y_j\\ \Delta v_{ij}=\eta\cdot err_o w_{jk} y_j (1-y_j)\cdot x_i \\ 寫成程式碼用向量批次計算的話就是如下所示\\ \Delta w=\eta\cdot (sum(D-O)\cdot O(1-O)) \cdot Y\\ \Delta v=\eta\cdot (sum(D-O)\cdot O(1-O)) W\cdot Y\cdot X \\$

任意層BP網路程式碼實現

參考這位老哥的程式碼： https://www.k2zone.cn/?p=1047

import numpy as np
def logistic(x):
    return 1/(1+np.exp(-x))
def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))

def tanh(x):
    return np.tanh(x)

def tanh_deriv(x):
    return 1.0 - np.tanh(x) * np.tanh(x)

class NeuralNetwork:
   #建構函式
   def __init__(self, layers, activation='tanh'):
       '''
       :param layers: list型別,比如[2,2.1]代表輸入層有兩個神經元,隱藏層有兩個，輸出層有一個
       :param activation: 啟用函數
       '''
       self.layers = layers
       #選擇後面用到的啟用函數
       if activation == 'logistic':
           self.activation = logistic
           self.activation_deriv = logistic_derivative
       elif activation == 'tanh':
           self.activation = tanh
           self.activation_deriv = tanh_deriv
       #定義網路的層數
       self.num_layers = len(layers)
       '''
       生成除輸入層外的每層中神經元的biase值，在（-1，1）之間，每一層都是一行一維陣列資料
       randn函數執行一次生成x行y列的資料
       '''
       self.biases = [np.random.randn(x) for x in layers[1:]]
       print("初始偏向：",self.biases)
       '''
       隨機生成每條連線線的權重，在（-1,1）之間
       weights[i-1]代表第i層和第i-1層之間的權重，元素個數等於i層神經元個數
       weights[i-1][0]表示第i層中第一個神經單元和第i-1層每個神經元的權重，元素個數等於i-1層神經元個數
       '''
       self.weights = [np.random.randn(y, x)
                       for x, y in zip(layers[:-1], layers[1:])]
       print("初始權重：",self.weights)

   #訓練模型，進行建模
   def fit(self, X, y, learning_rate=0.2, epochs=1):
       '''
       :param self: 當前物件指標
       :param X: 訓練集
       :param y: 訓練標記
       :param learning_rate: 學習率
       :param epochs: 訓練次數
       :return: void
       '''
       for k in range(epochs):
           #每次迭代都回圈一次訓練集
           for i in range(len(X)):
               #儲存本次的輸入和後幾層的輸出
               activations = [X[i]]
               #向前一層一層的走
               for b, w in zip(self.biases, self.weights):
                   # print "w:",w
                   # print "activations[-1]:",activations[-1]
                   # print "b:", b
                   #計算啟用函數的引數,計算公式：權重.dot(輸入)+偏向
                   z = np.dot(w, activations[-1])+b

                   #計算輸出值
                   output = self.activation(z)
                   #將本次輸出放進輸入列表，後面更新權重的時候備用
                   activations.append(output)
               # print "計算結果",activations
               #計算誤差值
               """
               下面這行程式碼參考公式8
               """
               error = y[i]-activations[-1]
               """
               計算輸出層誤差率
               參考公式9
			   """
               deltas = [error * self.activation_deriv(activations[-1])]

               #迴圈計算隱藏層的誤差率,從倒數第2層開始
               for l in range(self.num_layers-2, 0, -1):
                   # print "第l層的權重",self.weights[l]
                   # print "l+1層的誤差率",deltas[-1]
                   deltas.append(self.activation_deriv(activations[l]) * np.dot( deltas[-1],self.weights[l]))
               #將各層誤差率順序顛倒，準備逐層更新權重和偏向
               deltas.reverse()
               """
               更新權重和偏向
               參考公式3、4
               """
               for j in range(self.num_layers-1):
                   #本層結點的輸出值
                   layers = np.array(activations[j])
                   # print "本層輸出：",layers
                   # print "錯誤率：",deltas[j]
                   # 權重的增長量，計算公式，增長量 = 學習率 * (錯誤率.dot(輸出值))
                   delta = learning_rate * ((np.atleast_2d(deltas[j]).T).dot(np.atleast_2d(layers)))
                   #更新權重
                   self.weights[j] += delta
                   #print "本層偏向：",self.biases[j]
                   #偏向增加量，計算公式：學習率 * 錯誤率
                   delta = learning_rate * deltas[j]
                   #print np.atleast_2d(delta).T
                   #更新偏向
                   self.biases[j] += delta
               #print self.weights

   def predict(self, x):
       '''
       :param x: 測試集
       :return: 各型別的預測值
       '''
       for b, w in zip(self.biases, self.weights):
           # 計算權重相加再加上偏向的結果
           z = np.dot(w, x) + b
           # 計算輸出值
           x = self.activation(z)
       return x

nn = NeuralNetwork([2,4,3,1], 'tanh')
#訓練集
X = np.array([[0, 0], [0, 1], [1, 0],[1, 1]])
#lanbel標記
y = np.array([0, 1, 1, 0])
#建模
nn.fit(X, y, epochs=2000)
#預測
for i in [[0, 0], [0, 1], [1, 0], [1,1]]:
   print(i, nn.predict(i))

執行結果如

在這裡插入圖片描述

BP神經網路的詳細推導 與 完整程式碼

文章目錄