本文會以AI五子棋展開，講解一些強化學習中博弈方向的演演算法。
全文只涉及演演算法講解，不會展現程式碼。

蒙特卡洛樹搜尋 MCTS

隨著計算機算力的發展，利用隨機取樣的樣本值來估計真實值的蒙特卡洛方法 (Monte Carlo method) 得到了充分的發揮與利用。

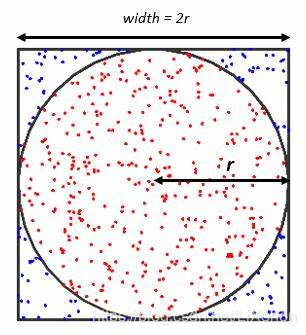
如上圖用蒙特卡洛方法以模擬面積比例，達到求出π的近似值的目的。

以五子棋舉例，在不考慮任何其他演演算法與規則的情況下，我們在一個棋局的空位黑白交替隨機落子，直至其中一方獲勝或滿棋盤。在這樣的隨機嘗試中我們會記錄雙方勝負並在有足夠大量的資料時依據勝率評價其中的每一步。這樣的演演算法好處巨大，它可以在理想情況下求出每一步的理論最大勝率解。

蒙特卡洛樹搜尋 (The monte carlo search tree) 又稱隨機抽樣或統計試驗方法，屬於計算數學的一個分支。在蒙特卡洛方法的基礎上，我們利用樹結構來更加高效的進行結點值的更新和選擇。

蒙特卡洛樹搜尋演演算法

一般來說，蒙特卡洛樹搜尋會有一個根結點。像這樣的根結點會有模擬後續選擇的子結點若干個。

以五子棋為例，若以正中的H8位元為根結點，棋盤大小為15 * 15，那麼根結點的後續子結點就會有15 * 15 - 1個。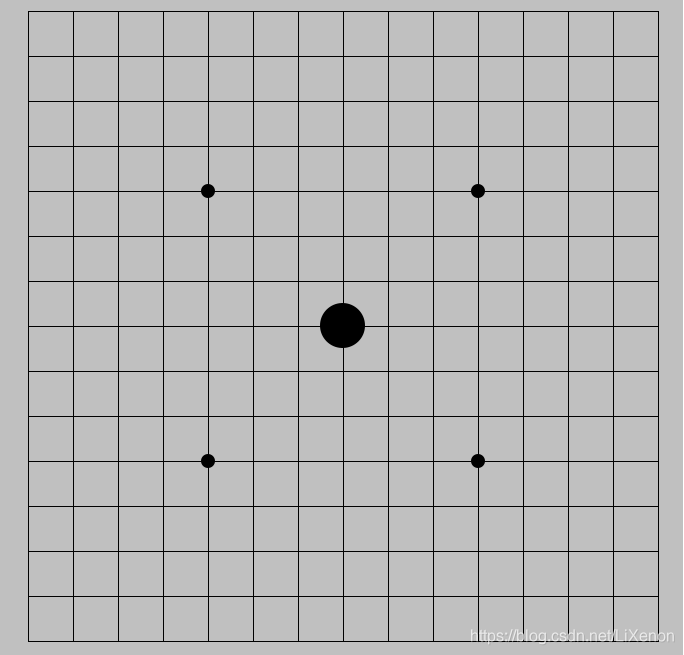
若是隨機落子，那麼這15 * 15 - 1中的某一個子結點會繼續被分配15 * 15 - 2個子結點。在棋局結束時，我們會利用反向傳播將結果返回各個參與結點，並以勝率評價該結點。隨著資料量的增加，每一步棋（每個結點）的勝率會被更加完善。

看起來已經大功告成，不過，這樣下來，我們的空間和時間複雜度會隨著回合數n變得越來越高，節點個數會達到接近$225^n$. 這樣的演演算法明顯需要耗費極大的計算空間。所以，我們將要用到UCT演演算法及基於minimax演演算法的alpha beta剪枝來減少結點的個數，同時，我們還可以用到一些小竅門，比如用估值函數來省去不必要的嘗試。

上限置信區間演演算法 UCT

UCT演演算法(Upper Confidence Bound Apply to Tree)是UCB演演算法(Upper Confidence Bound)在蒙特卡洛樹搜尋中的演演算法。UCB演演算法的背景起源於一種多臂老虎機(Multi-Armed Bandit)，可以追溯到上世紀三十年代。
多臂老虎機問題描述如下：

1. 老虎機有K個搖臂，每個搖臂以一定的概率吐出金幣，且概率是未知的
2. 玩家每次只能從K個搖臂中選擇其中一個，且相鄰兩次選擇或獎勵沒有任何關係
3. 玩家的目的是通過一定的策略使自己的獎勵最大，即得到更多的金幣

要是你是一個手持籌碼的賭徒，如何才能在付出最少的情況下找出回報概率最大的老虎機搖臂？UCB演演算法很好地解決了這個問題。想象一下，要是我們想要找出高回報的老虎機搖臂，就必須先把所有的老虎機搖臂嘗試到一定次數，再根據回報率將回報率高的搖臂的嘗試機會加大一些，直到資料足以確定出最高回報率的搖臂。UCB演演算法公式也就類似於以上的思考方法。

UCB演演算法公式：

$A=Vi+C\ast \sqrt{\frac{ln(n)}{Ni}}$

其中Vi表示第i個搖臂回報的次數，n表示所有搖臂的按壓次數，Ni表示按壓第i個搖臂的次數。C是常數，能調節高回報與高嘗試次數之間的權重。

回到我們五子棋中的例子來，要是上一次落子是父結點，那麼作為所有落子可能的子結點就相當於之前的k個搖臂。我們給每個子結點一個置信度A，那麼Vi就是第i個子結點獲勝的次數，n為所有子結點的嘗試次數，也就是父結點的嘗試次數，Ni為第i個子結點的嘗試次數，在這裡我們的C一般取$\sqrt{2}$。

我們每次嘗試都會選擇置信度最高的子結點。在一開始時，置信度高的結點一般是被選擇次數少的結點，這樣能夠達到多次嘗試所有子結點的目的。在嘗試一定次數後，勝率高的結點會更有機會被再次嘗試，達到篩選高勝率子結點的目的。這就是應用於MCST中的UCT演演算法。

Minimax演演算法與納什均衡

我們在得到每一步的勝率後，就可以讓AI根據當前每一步的勝率來和我們對戰。不過，以當前勝率最大的結點為下一步就一定是最優的選擇嗎？假如你是AI，與你對弈的是能力不輸於你的人類，你通過演演算法計算出瞭如圖的三步所有結點中AI的勝率，圖中的root為人類落子，你恪守最高勝率的信條進行選擇，最後勝率會有多大？

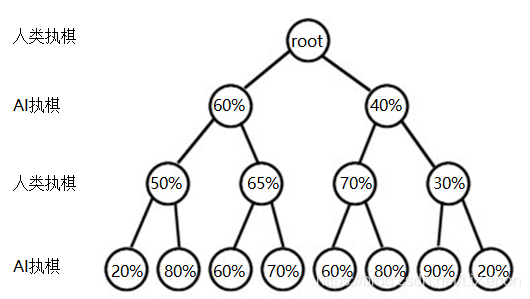
很明顯，AI在第一次做出選擇時，會選擇勝率為60%的結點，而棋藝高超的人類則會選擇看似吃虧的65%（此處是AI勝率）結點，給AI留下60%勝率和70%勝率的兩個選擇。所以，最後AI的勝率只有70%。

要是AI能夠看得更加長遠，只盯著第三步的90%勝率的結點落子，AI能做到90%勝率的最終結果嗎？不能。因為人類會在AI選擇40%勝率的結點後著70%勝率的棋，AI最高只會有80%的最終勝率。

五子棋屬於一種完備資訊零和博弈。如果我們的對手足夠聰明，依靠所有已知資訊，每次都會做出最優判斷，像上面有限步數的棋局預測中，我們能夠做到納什均衡 (Nash equilibrium)。

對此也誕生了Minimax演演算法。不妨假設圖中正三角為自己，倒三角為對手，三角的子結點是可供選擇的方案。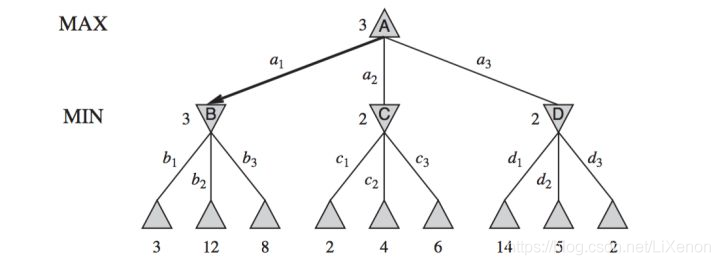
我們自己想要選到結果最大的方案，對手想盡可能阻止我們選擇結果大的方案，那麼從下往上看，對手的每一步一定選擇結果最小的方案，即B走b1選3，C走c1選2，D走d3選2——對手步對應MIN，選擇結果最小的方案。而我們自己只能走a1選3，對應MAX，選擇可選結果中的最大方案。

Minimax演演算法一般是區域性的，因為算力的限制我們無法考慮到全域性情形。正如同棋類大師能推算棋局的後幾步，我們可以通過後三步或後五步的預測來找到目前最適合我們的選擇。不過，像後五步預測（六層思考）這樣對算力的要求還是太高，我們還能不能再減少一些不必要的結點？

alpha beta剪枝

在培養果樹時，我們會剪掉重疊多餘的樹枝來減少果樹對能量的消耗，使總光合作用效率最大化。在蒙特卡洛樹中同樣如此。

以Minimax演演算法為基礎，alpha beta剪枝 (Alpha Beta Pruning) 能在理想情況下上將結點複雜度n減少至$\sqrt{n}$，在隨機情況下減少至$n^{\frac{3}{4}}$.

alpha beta剪枝演演算法是怎麼減去結點的呢？

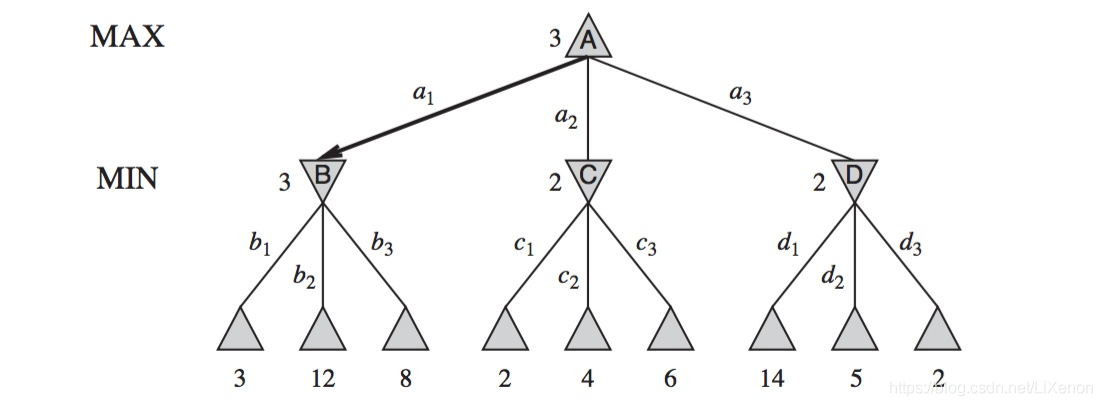
我們給每一個非葉子結點一個alpha值與一個beta值，圖中以[alpha, beta]表示，初始alpha beta為[-∞, +∞]。整體為先左子樹，返回父結點，再右子樹（多叉樹時為先第一個子樹到父結點，再從到第二個子樹，從第二個子樹到父結點……以此類推）。其中從子到父時，父結點中MIN層選自己的beta、子結點中alpha或beta最小，賦給beta；MAX層選自己的alpha、子結點中alpha或beta最大，賦給alpha。從父到子時，父結點中的alpha與beta傳遞給子結點。當alpha大於等於beta時剪枝。

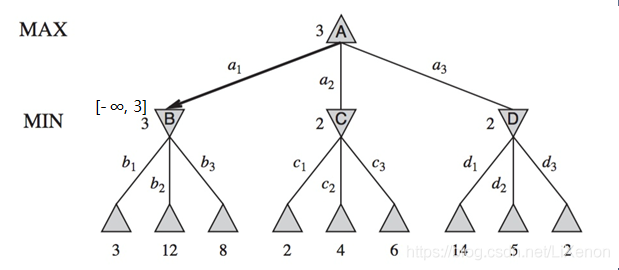
從最左下角3開始。B屬MIN層，選擇最小值3向上賦給beta（注意，此時只有3，12和8的葉子結點未知），B[-∞, 3]. 向下到值為12和8的結點，不變。

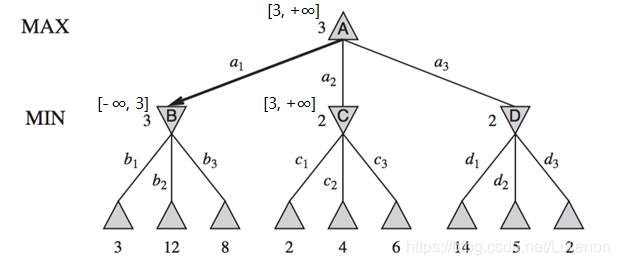
A屬MAX層，選擇最大值3賦給alpha，A[3, +∞]. C的alpha與beta傳遞於A，C[3, +∞].

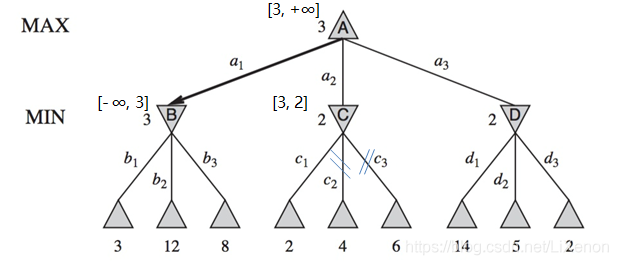
由於C的子結點中2最小，C屬MIN層，將2傳遞給beta，C[3, 2]. 由於3大於2，其後值為4的子結點和值為6的子結點被剪枝。C向上到A，A屬MAX層，A[3, +∞]不變。

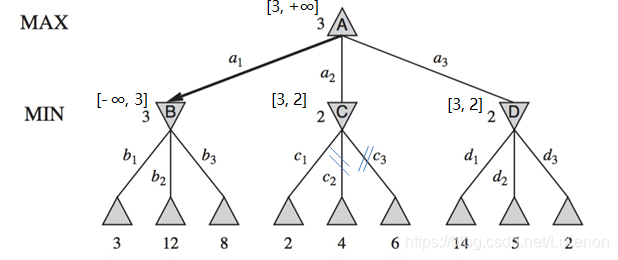
A向下到D，D[3, +∞]. D屬MIN層，先看14，取最小14賦給D的beta，D[3, 14]. 再看5，5不改變D。最後看2，取最小2賦給D的beta，D[3,2]. 由於3大於2，理應剪枝，但由於後面無兄弟結點，不剪枝。返回A，A屬於MAX層，A[3, +∞]不變。到此，alpha beta剪枝完畢。

估值函數

雖有UCT演演算法與alpha beta演演算法減少大量計算，但是蒙特卡洛樹搜尋的隨機取樣仍然會耗費大量不必要的算力。如果我們能夠提前對子結點進行下子價值的估計，多嘗試高價值結點，少嘗試或不嘗試低價值結點，那麼我們的算力會傾向於更值得嘗試的方向。

1. 首先遍歷每一個子結點，進行估值計算
2. 該點向左遍歷，出現連續同色的棋子，進行加1，cnt++
3. 返回該點向右遍歷，出現連續同色的棋子，進行加1，cnt++
4. 若兩邊無封堵，則權重為cnt * cnt顏色的值（白 1，黑 -1）
5. 若一邊出現封堵，則權重cnt * cnt顏色的值 / 4
6. 若兩邊封堵，則權重為0
7. 若 cnt 大於等於5，權重為最大值 * 顏色的值（白 1，黑 -1）
8. 其他方向同樣計算一遍，總權重是每個點四個方向（行、列、左右對角線）的權重之和

優化與總結

要判斷多連子與有無封堵需要四個方向簡單的遍歷，這裡不再贅述。

估值函數可以結合改良UCT演演算法，讓AI儘可能多地嘗試高價值結點，少嘗試低價值結點，不嘗試無價值結點。估值函數同樣可以應用於alpha beta剪枝，一般比基於勝率的alpha beta剪枝耗時更短。

本篇部落格借用到了很多其他人的經驗與思想，在此表示感謝。要是有更好的意見和建議，還請批評指正。