Lorenz混沌系統建模與電路模擬實現
混沌是確定性非線性系統中產生的一種偽隨機行為,呈現初值敏感性。隨著混沌理論在通訊與雷達等工程領域得到日漸廣泛地應用,構建實際的混沌系統,產生混沌訊號成為近來研究領域的一個熱點。混沌系統的實現為混沌理論應用奠定了重要的基礎,並推動了混沌理論研究的進一步發展。
本論文首先總體上介紹了本課題的研究背景和研究意義,然後具體地解釋了混沌的一些基本概念。闡述各種混沌系統族數學模型的建立、理論分析、電路實現方法和模擬結果,特別是基於Matlab的Lorenz混沌系統建模與電路模擬實現,重點討論了Lorenz混沌系統的相關理論。最後由於本文詳細介紹了一種基於FPGA技術的Lorenz混沌訊號發生器,並對系統進行了模擬。
混沌是當今世界的前沿課題,它揭示了自然界和人類社會中普遍存在的複雜性:有序與無序的統一,確定性與概率性的統一,大大開拓了人們的視野,加深了對客觀世界的認識。混沌的發現,乃是繼二十世紀相對論與量子力學之後的第三次物理學大革命,這場革命正在衝擊和改變著幾乎所有的科學和技術領域,向我們提出了巨大的挑戰。
混沌科學首先向我們提出這樣一個帶有根本性質的問題:人們是生活在一個確定性的宇宙中,還是生活在一個概率性的宇宙中?這是科學家和哲學家們長期以來所探討的一個對世界帶有根本性看法的重要問題,但一直未能得到完滿的解決。混沌理論正在縮小這兩個對立描述體系之間的鴻溝:混沌是確定性系統的內在隨機性,是確定性與概率性辯證統一的世界。混沌運動乃是自然界中的一種基本的運動形態之一。
混沌究竟有何應用前景?這是擺在當今世介面前的重大課題。由於混沌的奇異特性(奇怪吸引子),特別是對初始條件極其微小變化的高度敏感性和不穩定性,即所謂的「差之毫釐,失之千里「的緣故,使得長期以來人們總是認為混沌是不可靠和不可控的,因而是無法應用的怪物,在應用及工程領域以往總是採取迴避和抵制的態度。例如,人們在電子系統的分析和設計中總是想方設法避免混沌的出現,力求系統的穩定性和可靠性。這種對混沌的片面認識與思維模式長期以來制約了混沌理論的發展與應用。由此人們聯想到前二次物理學革命所經歷的過程與此有很大的相似性。九十年代以來在國際上混沌的控制及同步理論的突破性進展,由此激發起來的理論與應用研究得到迅速發展,使得混沌的應用與發展出現了契機。通過對混沌較深層次的研究,人們發現混沌是可控制和同步的。特別值得一提的是:混沌同步及混沌控制方法,在1990年由美國海軍實驗室研究人員Pecora和Carroll等人提出,使得混沌在通訊領域中的應用成為可能,這一歷史性的重大發現將使混沌應用於通訊領域成為可能,導致了二十一世紀的一種全新的通訊方式—混沌同步通訊,被譽為混沌理論與應用的一個新的里程碑,從此揭開了混沌同步通訊的新篇章。從混沌理論的產生與形成到混沌的控制與應用這一歷史發展程序充分說明:混沌科學正在改變人們以往的思維模式,豐富和發展了人們的自然觀和認識論陣。
1.2 課題研究的目的和意義
混沌學研究對現代科學發展產生了巨大的影響。混沌學研究從其早期探索到重大突破,以至到本世紀70年代以後形成世界性研究熱潮,其涉及的領域包括數學、物理學、化學、生物學、氣象學和經濟學等眾多學科,其研究的成果滲透和影響著現代科學的幾乎整個學科體系。混沌學的研究揭開了現代科學發展的新篇章。混沌研究對於現代科學的影響不僅限於自然科學,而且涉及到經濟學、社會學、哲學及諸多人文科學,可以說幾乎覆蓋了一切學科領域。凡是涉及動力學過程的研究領域,大多都會發現混沌,都需要應用混沌動力學的研究成果。在傳統的經典科學領域,若按照混沌觀點重新考察,就會發現新現象,提出新問題、建
立新原理:而在一些非經典科學領域,運用混沌理論則可以解釋以往無法解釋的現象,可以處理歷來無法處理的資料,甚至形成一批新的學科分支。混沌對於現代科學更深刻的影響,主要在於在廣闊的科學領域裡推翻了經典理論的一些基本假設,改變了那些領域的研究方法,將可能孕育成一場科學大革命。混沌學研究還革新了經典的科學觀。在混沌發現之前,人們長期以為確定性系統排斥隨機性,隨機性只是某些複雜系統的屬性。然而混沌研究表明:一些完全確定性的系統,不外加任何隨機因素,初始條件也是確定的,但系統自身卻會內在的產生隨機行為,而且即使是非常簡單的確定系統同樣具有內在隨機性。混沌揭示的隨機性存在於確定性之中這一科學事實,最有力的說明客觀實體可以兼有確定性和隨機性;從牛頓到愛因斯坦都認為世界在本質上是有序的,有序等於有規律,無序就是無規律,系統有序和無序是截然對立的。這個觀點幾個世紀以來一直為人們所贊同,但是混沌和分形的發現和研究表明,混沌既包含有序又包含無序,混沌既不是具有周期性和其他明顯對稱性的有序態,也不是絕對的無序,而可以認為是必須用奇怪吸引子來刻畫的複雜有序,是一種蘊涵在無序中的有序。
混沌研究還對傳統方法論的變革有重大貢獻,其中最突出的是從還原論到系統論的轉變。經典的還原論認為,整體的或高層次的性質還可以還原為部分的或低層次的性質。然而隨著近代科學的發展,包括對混沌現象的探索,還原論到處碰壁。上世紀50年代,系統論思想開始形成,主張把研究的物件作為一個系統來處理。混沌是系統的一種整體行為,混沌學的研究成果成了系統論的有力佐證。整體觀和系統論正隨著混沌學一起擴充套件到各個現代學科領域,為現代科學的革命性變革做著方法論的準備。混沌作為當今舉世矚目的前沿課題及學術熱點,不僅大大拓展了人們的視野並加深了對客觀世界的認識,而且由於混沌的奇異特性,還促使人們研究在現實生活中控制和利用混沌的方法。近年來,國際上混沌同步及混沌控制的研究己取得了一些突破性進展,前景十分誘人。我們完全有理由相信,混沌的進步不僅孕育著深刻的科學革命,而且一定會促進社會生產力的大力發展,對人們的生活和生產產生巨大的根本性影響。
Lorenz在1963年洛倫茲在研究大氣對流現象時,發現了第一個結構簡單的三維自治混沌系統,這就是著名的「蝴蝶效應」模型,其數學模型為:

當r≤1時,對所有的x,y,z都成立,等式僅在r<1,x=y=z=0和r=1,x=y,z=0時才成立。
當r>1時,系統開始出現不穩定性,當r增加至rc時,有一個亞臨界的Hopf分岔。
當r>rc時,在吸引子附近相鄰的軌道平均來說是以指數分離的,所以兩條開始在一起非常接近的軌道很快喪失所有的相關性,呈現混沌狀。


5.2 Lorenz混沌系統的MATLAB模擬
在MATLAB環境下執行以上程式程式碼,輸入程式執行起點(x0,y0,z0),程式執行時間(t0,tf),引數(a,b,r)後,可得到三維相平面圖模擬結果,如圖5-1所示。
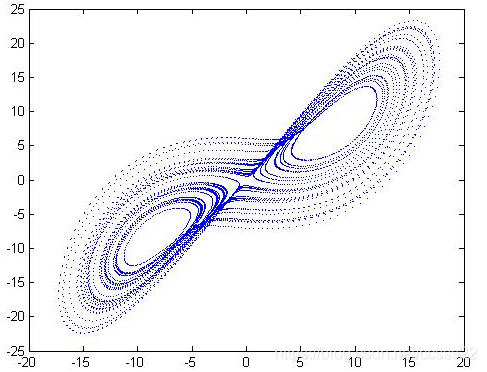
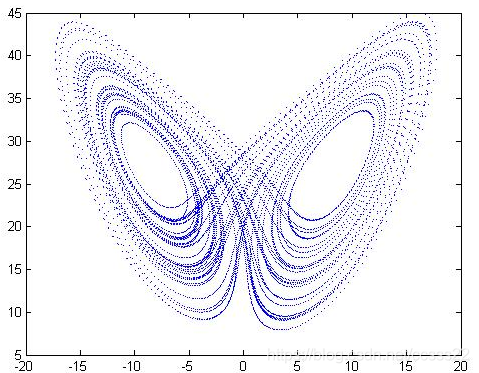
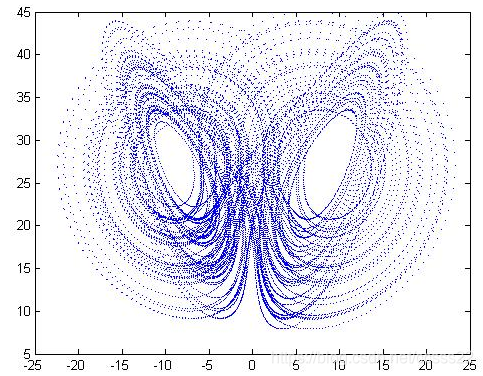
圖5-1 x-y面,y-z面,y-z面
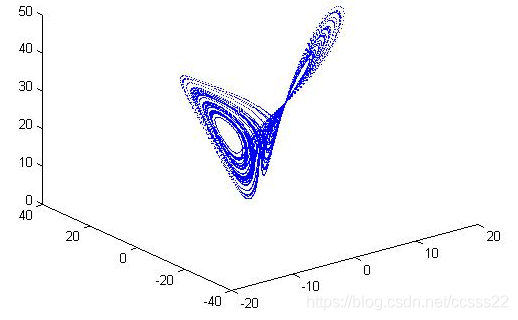
圖5-2 Lorenz相平面圖
將係數進行量化,假設1量化後為1111_1111_1111_1111_1111_1111,即FFFFFF,那麼我們可以得到
0.99 : FD70A2;
0.01 : 028F5C;
0.028 : 072B02;
0.001 : 004189;
0.999 : FFBE75;
0.9973333: FF513B;
這裡的計算結果均為24位元,所以在FPGA中編寫硬體描述語言的時候,我們也要採用24位元的計算方法。當乘法器相乘得到48位元結果的時候,通過截位得到24位元結果。然後參與下一級的運算。
6.2.1乘法器
該乘法器,我們採用IP核來完成。
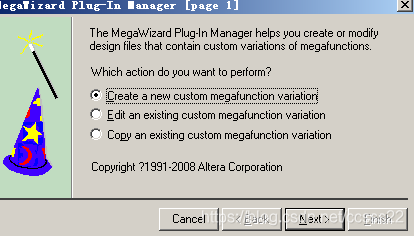
圖6-2 乘法器IP核生成步驟1
下一步:
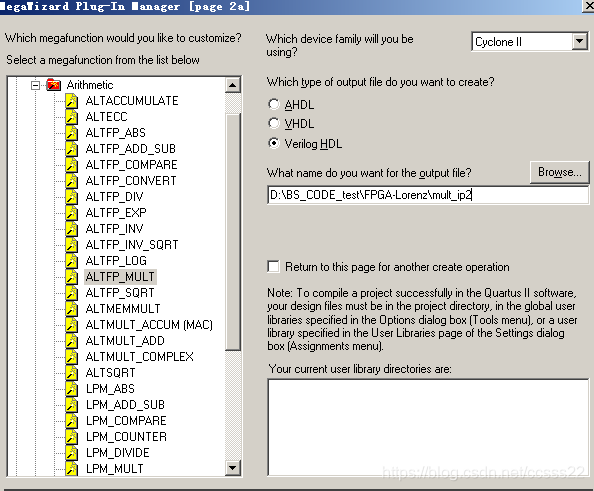
圖6-3 乘法器IP核生成步驟2
下一步:
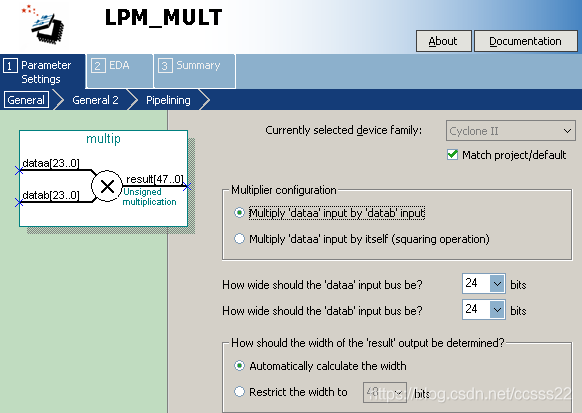
圖6-4 乘法器IP核生成步驟3
下一步:
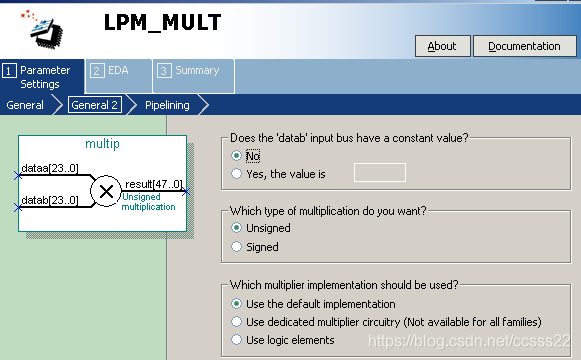
圖6-5 乘法器IP核生成步驟4
下一步:
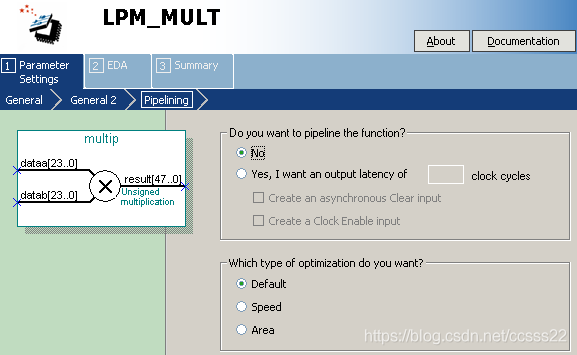
圖6-6 乘法器IP核生成步驟5
完成,對該核進行模擬,模擬結果如下所示:

圖6-7 乘法器IP核模擬
6.2.2加/減法器
這個模組比較簡單,只要用簡單的程式碼就能實現。這裡我們就不做具體的介紹了。其模擬結果如下所示:
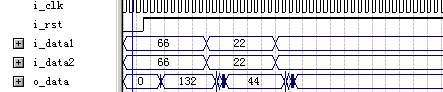
圖6-8 加法模擬結果

圖6-9 減法模擬結果