格密碼學習，抽代基礎學習（二）
今天找到了一個比較新手友好的slides，結合lec1和學姐的筆記一起看~
full-rank lattice 滿格
R
n
\mathbb{R}^{n}
Rn的概念：n維度實數集，每個元素是n維向量,向量中的每個分量是實數
Z
n
\mathbb{Z}^{n}
Zn的概念：n維度整數集，向量中每個分量是整數
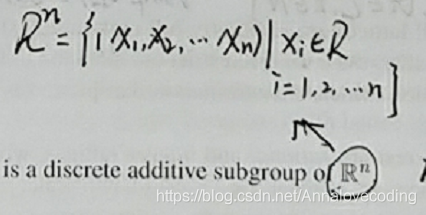
格(lattice)是一種數學結構，定義為一組線性無關的非0向量（稱作格基）的整係數線性組合。具體來說，給定一組格基
x
1
,
…
,
x
n
x_{1}, \ldots, x_{n}
x1,…,xn，對任意的整數
c
1
,
…
,
c
n
,
c
1
x
1
+
…
+
c
n
x
n
c_{1}, \ldots, c_{n}, \quad c_{1} x_{1}+\ldots+c_{n} x_{n}
c1,…,cn,c1x1+…+cnxn都是屬於這個格的向量，
n
n
n稱為格的維數。例如，下圖表示了一個二維格和兩組不同的格基：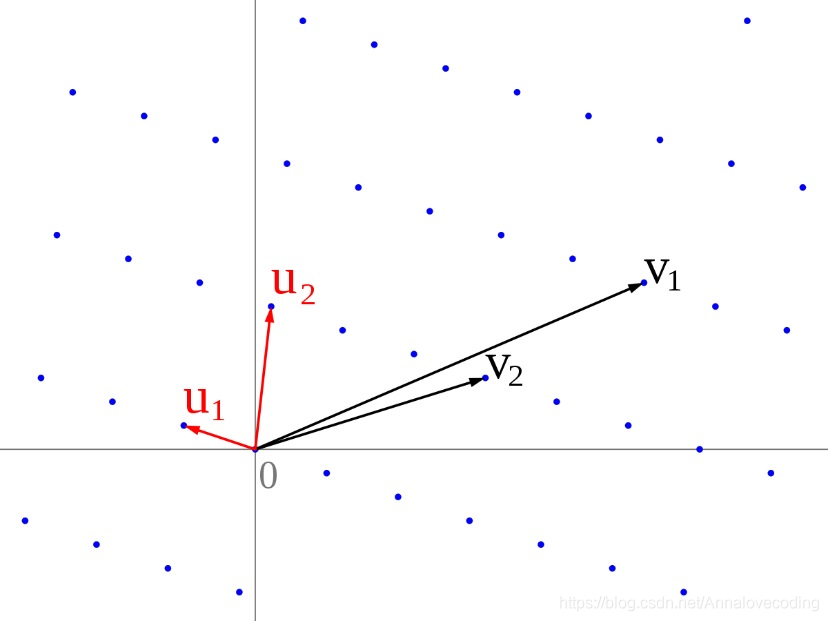
一個格的格基可以不是唯一的，例如((2,1),(1,1))和((1,0),(0,1)）都是二維整數格的一組格基，即使定義了同樣格的兩組格基，長度也可能相差很大。一個維數足夠高的格，通過一組隨機選取的格基找到一組短格基或得到一組線性無關的短格向量是困難的。
單點集0也是格
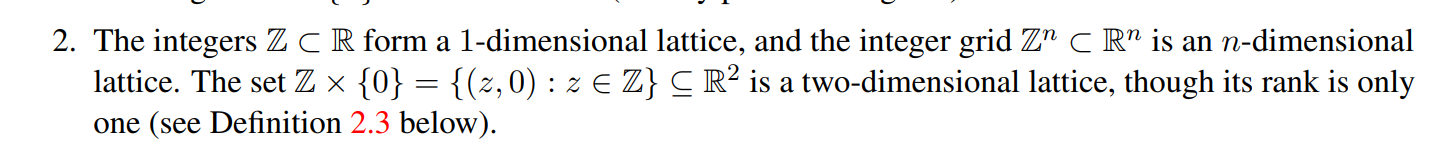
整數構成一維格，n格整數是一個n維格，整數和單點集0的笛卡爾積是一個二維格，雖然他的秩為1。
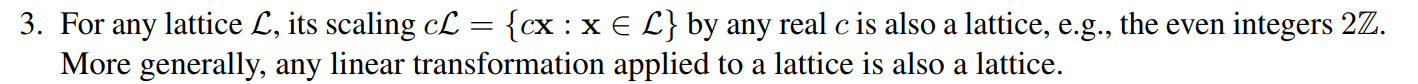
3、任何的格
L
\mathcal{L}
L，他的c倍
c
L
=
{
c
x
:
x
∈
L
}
c \mathcal{L}=\{c \mathbf{x}: \mathbf{x} \in \mathcal{L}\}
cL={cx:x∈L}，（c是實數）也是格。一個格的線性變換依然是格
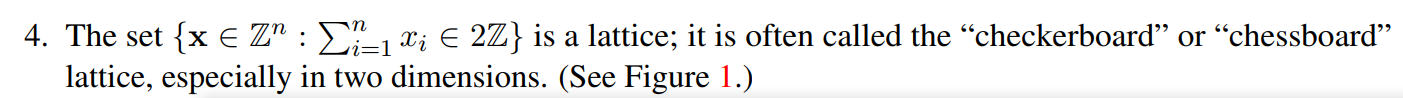4.集合
{
x
∈
Z
n
:
∑
i
=
1
n
x
i
∈
2
Z
}
\left\{\mathbf{x} \in \mathbb{Z}^{n}: \sum_{i=1}^{n} x_{i} \in 2 \mathbb{Z}\right\}
{x∈Zn:∑i=1nxi∈2Z}也是一個格，通常被稱為棋盤格。
如下圖所示
5、有理數Q不能構成格，雖然他們可以構成子群，但是不是離散的。存在任意接近0的有理數。
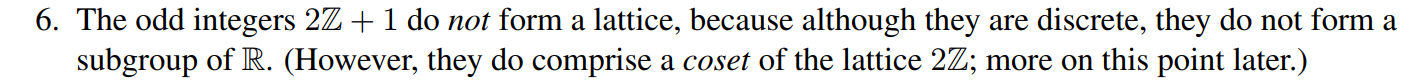6、奇數2 \mathbb{Z}+1也不構成格，儘管他們是離散的，但是他們不能組成R的子群。
7、群G=
Z
+
2
Z
\mathbb{Z}+\sqrt{2} \mathbb{Z}
Z+2Z並不是格，因為他不是離散的。
定義 格
L
⊂
R
n
\mathcal{L} \subset \mathbb{R}^{n}
L⊂Rn的秩k是他的線性空間的維度。
k
=
dim
(
span
(
L
)
)
k=\operatorname{dim}(\operatorname{span}(\mathcal{L}))
k=dim(span(L))。當k=n的生活，格是滿秩的。
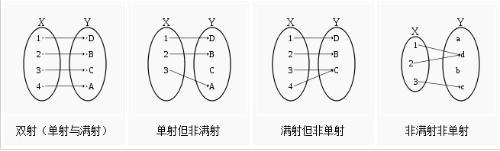
同態對映例子
定義設
ϕ
\phi
ϕ是集合A到B的一個關於運算A和運算B的同態對映，若
ϕ
\phi
ϕ是一個單射（滿射）
則稱
ϕ
\phi
ϕ是一個同態單射（同態滿射）
同構、自同構
A和B是同構集合
如果一個對映是A到B的同構對映，則逆對映也是同構對映。
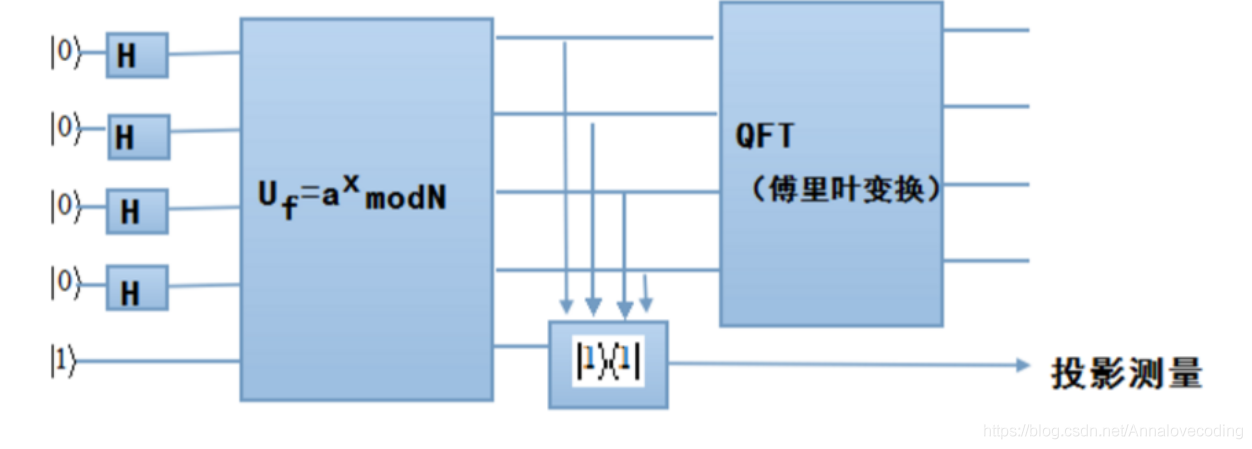
Shor演演算法
整數分解的指數時間量子計算機演演算法，用於解決給定的一個整數N，找出他的素因子。Shor演演算法的效率歸因於量子傅立葉變換的效率，以及通過重複平方得到的模冪。
英語名詞
rank 秩
rationals 有理數
linear span 線性空間
bijectively 雙射地
