00摘要

針對2020年第十五屆全國大學生智慧車競賽信標組關於聲音信標的識別，需要採集聲音訊號和FM訊號，通過聲音訊號和FM訊號互相關進行距離檢測和通過兩組聲音訊號互相關進行信標方位判斷。

實際中，是在頻域中對兩組訊號做乘法求最大值，而將時域訊號變換為頻域訊號需要經過FFT變換，本系統引入一種新的級聯FFT變換，大大提高了計算速度和效率。為了增加系統的抗干擾性，我們使用了廣義互相關演演算法，有效抑制了噪聲和混響的干擾。

關鍵詞：級聯FFT；廣義互相關；計算速度；

01引言

快速傅立葉變換(FFT)本身便是利用了離散傅立葉變換(DFT)中的對稱性和週期性，大大縮短了傅立葉變換的時長，這使得FFT成為基本的訊號處理演演算法。

在2020年第十五屆全國智慧車競賽中，信標組的比賽模式發生了很大的變化，從原始的識別一定頻率的光訊號變為週期性的250~2000Hz的Chirp聲音訊號和對應的FM調頻訊號。信標發出的訊號的變化導致了訊號識別和處理模式的變化，由原來識別光訊號使用攝像頭，變為接收聲音訊號的麥克風模組及接收FM訊號的FM解調模組，經過不斷嘗試和選擇，麥克風我們使用了9814帶自動增益的麥克風模組，FM解調模組使用了RDA5807解調晶片，兩者在實際使用中都取得了非常好的效果。

在訊號處理中，一定距離的麥克風接受到的訊號進行互相關可以獲得聲源方位，緊挨著的FM模組和麥克風接受到的訊號進行互相關可以得到車身與信標的距離。時域互相關運算計算量是十分龐大，實際上可以看做是兩組離散訊號的時域折積運算，因此一般我們會把這種折積運算轉換到頻域中，將時域折積等效為頻域相乘，這樣會大大簡化我們的計算。將時域訊號變換到頻域一般使用快速傅立葉變換(FFT)，但在實際使用中這種速度仍然無法滿足高速定位的需求。我們選用了TC264DA晶片的核心板，與普通TC264D晶片不同，TC264DA擁有512K的EMEM記憶體空間和內建了硬體FFT計算資源，硬體FFT比軟體FFT在速度上有質的提升。但其存在的缺點為硬體FFT只能計算整形資料，會造成一定程度的精度丟失，並且硬體FFT最多隻能計算1024個點的，這種精度不能滿足本次比賽中信標的識別。在本次比賽中至少要使用2048點的FFT，才能在高速下準確定位。為了解決此問題，我們引入了一種新的級聯FFT變換，既使用1024點的硬體FFT又能彌補序列長度不夠的缺陷，並在此基礎上融合入廣義互相關，提升互相關的抗干擾性。

02級聯FFT演演算法

級聯FFT演演算法的基本思想是把長序列進行分段，類似於把一維陣列變為二維陣列，然後對行和列分別進行FFT變換，用一定的計算方法將多個短序列的FFT合成原長序列的FFT結果。

直接把一段C=M×N點序列訊號x(n+mN)，n=0,1,2,…,N-1;m=0,1,2,…,M-1;當做一維序列進行FFT變換，運算結果可以表示為：

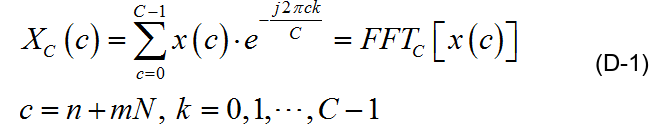
把一段C=M×N點序列訊號x(n+mN)，n=0,1,2,…,N-1;m=0,1,2,…,M-1;當做二維獨立序列進行FFT變換，也就是先進行行方向N點的FFT運算，再進行列方向M點的FFT運算，兩者序列編號不相關，運算結果可以表示為：

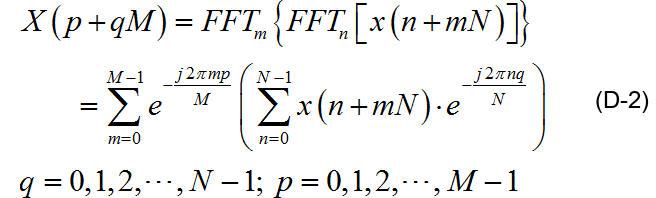
當把這段序列看做一維序列排列為二維序列時，序列編號將會發生變化，對應的FFT運算公式也會發生變化，運算結果表示為：

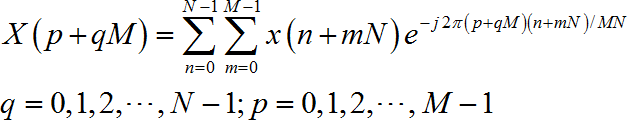
化簡後得：

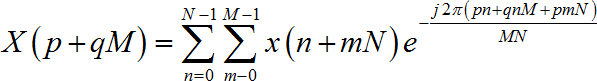
可以看出(1-4)和(1-2)只相差e^(-j2πnp/N)，也就是隻要使e^{(-j2πnp/N)=1}即可使兩者相等，但實際上，e^(-j2πnp/N)不可能一直等於1。

03交叉項補償

根據分析，獨立的二維序列行和列進行級聯FFT運算和一維序列排列成二維序列再進行行和列的級聯FFT運算，兩者相差一個補償因子e^(-j2πnp/N)，在實際中，我們只需在中途乘上補償因子即可使兩者等效。

由FFT運算的線性性質可以得到，矩陣化後的資料進行FFT運算時，行和列運算順序不同不會影響最終的結果。將兩維的運算順序調換後，也就是先進行列方向的FFT變換，再進行行方向的FFT運算，運算結果可以表示為：

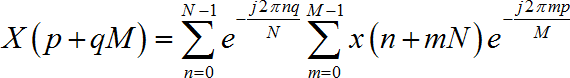
進行了列變換後，就需要加入補償因子，運算過程如下：

化簡後得：

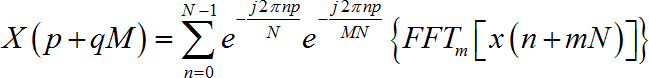
綜上，級聯FFT具體過程為：首先將一維序列排列為二維序列M行N列，首先對每行進行FFT變換，對每個元素乘以補償因子e^(-j2πnp/N)，然後對每列進行FFT變換，最後按列取出即為原一維序列FFT變換後的結果。

04.MATLAB模擬

在本次競賽中，我們使用了2048點的聲音訊號做互相關，並在頻域相乘之後進行頻域補零，補為4096個點，然後使用級聯IFFT變換取最大值，即得到互相關最終結果。

我們取樣了一組FM解調訊號進行了一系列模擬實驗，通過該訊號和該訊號的延時訊號模擬FM和麥克風的互相關運算。首先是使用普通的FFT進行互相關實驗，原始FM訊號和延遲的FM訊號波形圖如圖D-1所示，兩者的普通的FFT變換波形如圖D-2所示，互相關結果如圖D-3所示，使用MATLAB求互相關結果最大值，最大值點為第201點，設定的延遲為100點，因為在頻域中進行了補零操作，所以互相關結果精度是原始點數的兩倍，實驗結果正確。

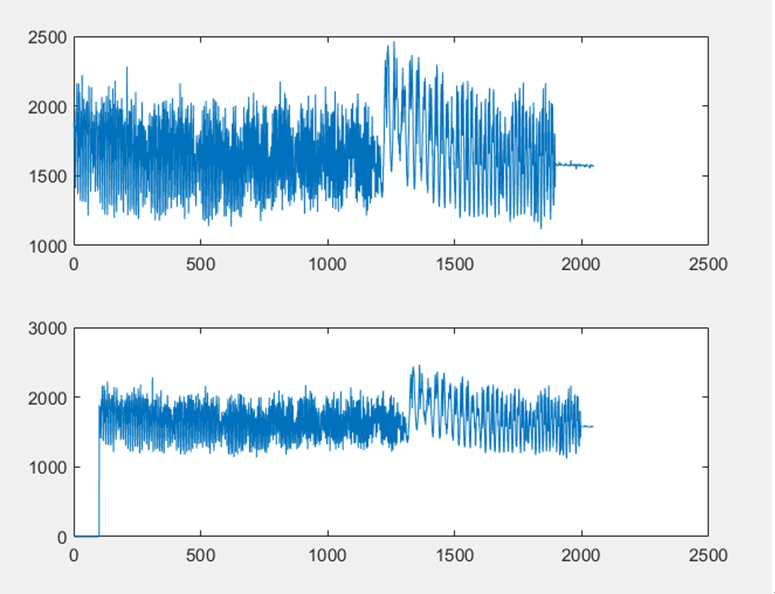
^{▲ 普通FFT下FM訊號波形和100點延遲的FM訊號波形}

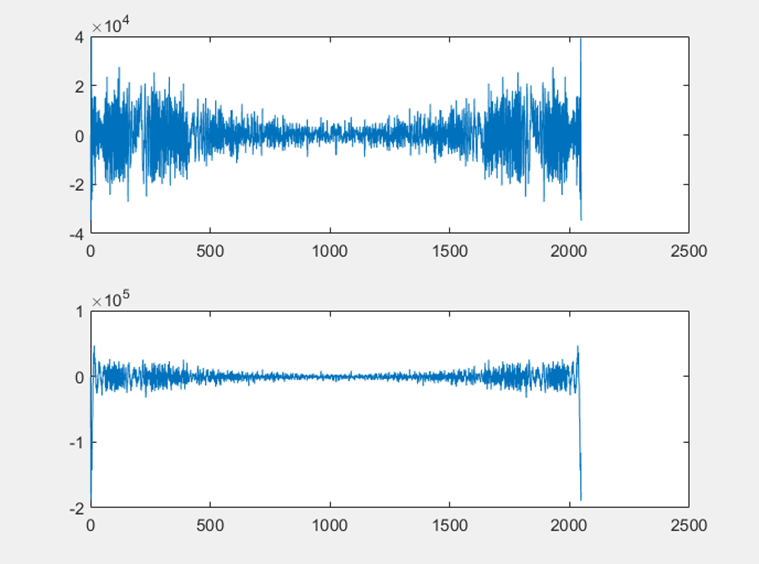
^{▲ 普通FFT下的兩訊號FFT變換}

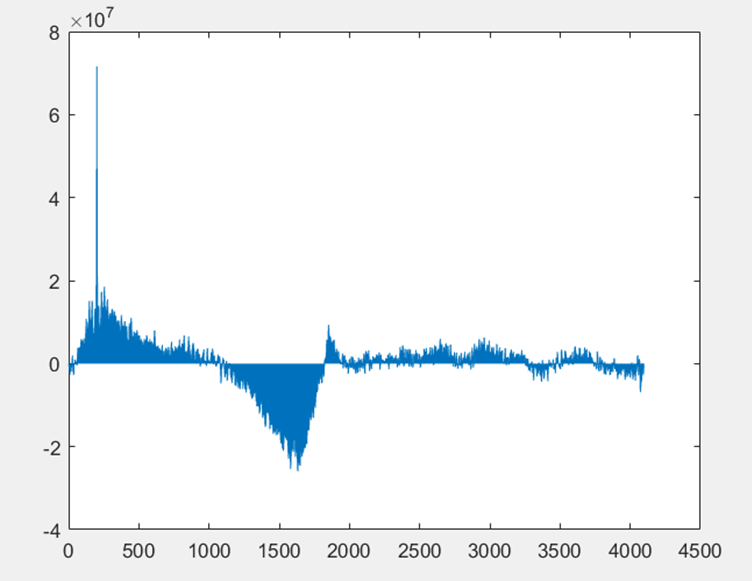
^{▲ 普通FFT下兩訊號互相關結果}

同理，我們使用級聯FFT，首先把2048點放置為兩行1024點，先對列進行兩點FFT變換，再對所有點數乘以補償因子，接著對每行進行1024點的FFT變換，最後按列取出即可。然後進行互相關運算，接著把2048點的結果補零為4096。然後把4096點按列排列為4行1024點，進行級聯IFFT運算，級聯IFFT可以看做級聯FFT的逆運算。運算步驟類似這裡不進行展開了。MATLAB模擬結果如下，FM訊號和FM延時訊號如圖D-4所示，兩者級聯FFT變換如圖D-5所示，最終互相關結果如圖D-6所示，使用MATLAB求最大值點，對應為第201點

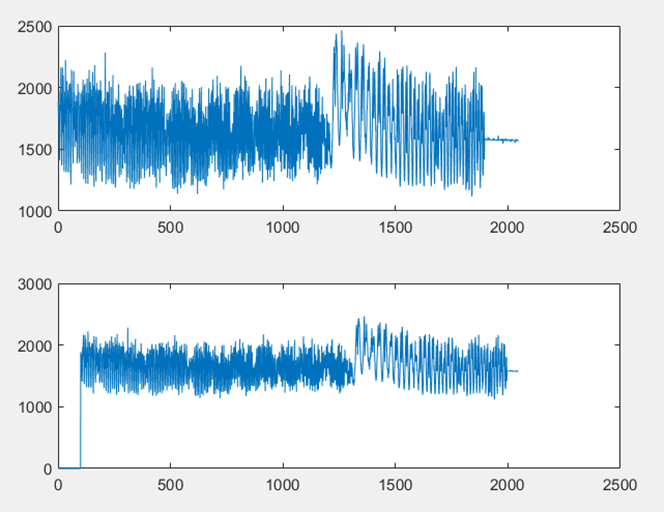
^{▲ 級聯FFT下FM訊號和100點延時的FM訊號波形}

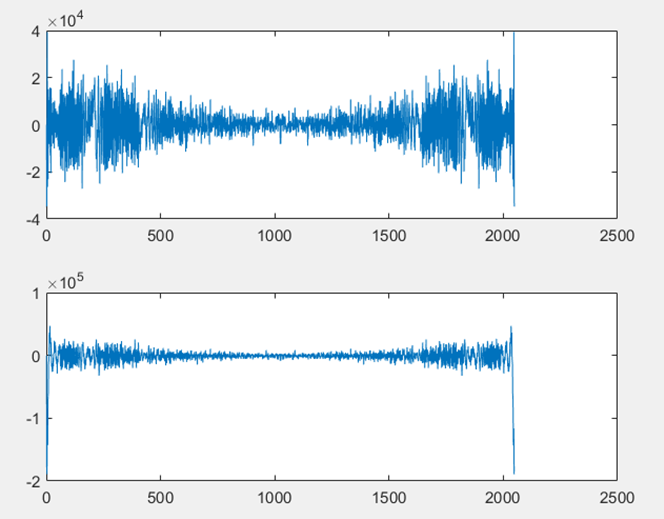
^{▲ 級聯FFT下兩訊號級聯FFT變換後的波形}

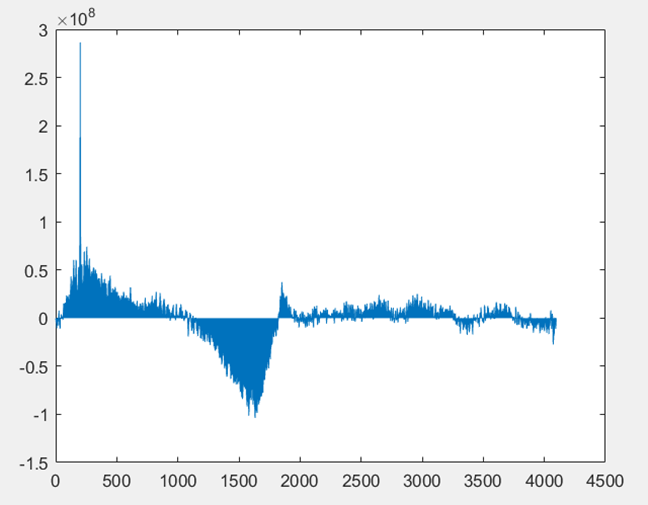
^{▲ 級聯FFT下兩訊號互相關結果}
從上面結果可以看出，級聯FFT運算結果和普通FFT運算結果完全一致，兩者是等效的，然而把級聯FFT運用到帶有硬體FFT的MCU中就可以節省大量的運算時間，把軟體運算轉化為硬體計算，大大提高了運算速度和運算效率.

05廣義互相關

在實際使用麥克風時，很容易受到輪子噪聲，空氣中的噪聲，以及牆面反射等的影響，這會使接受到的訊號產生失真，無論是線性失真還是非線性失真都會給我們的互相關結果帶來巨大影響。

類似於前面所說的基本互相關方法，廣義互相關演演算法估計得到的時延同樣對應於兩個麥克風接受到的訊號之間的相關函取得最大值的位置。

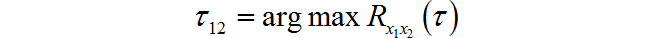
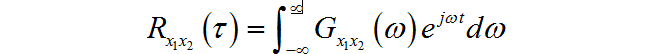
上面式子中，${\tau }_{12}$是兩個訊號之間的延時，$G_{x1x2}\left(\omega \right)$是$x_1\left(n\right)$和$x_2\left(n\right)$的互功率譜。$X_1\left(\omega \right)$是$x_1\left(n\right)$的傅立葉變換，$X_2\left(\omega \right)$是$x_2\left(n\right)$的傅立葉變換。

減弱或消除實際環境中噪聲、混響的影響，可以在互功率譜頻域中使用加權函數給予一定加權，再經過IFFT變換後得到廣義互相關結果，廣義互相關函數表示式為：

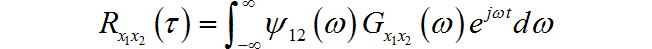
${\psi }_{12}\left(\omega \right)$為頻域加權函數，加權函數不同，實際效果也會有差異，實際應用中，可以針對噪聲和混響情況選取不同的加權函數，使相關函數峰值尖銳化，從而使得估計值更加準確。加權函數的選取主要有互功率譜相位（PHAT），ROTH處理器和平滑相干變換（SCOT）。

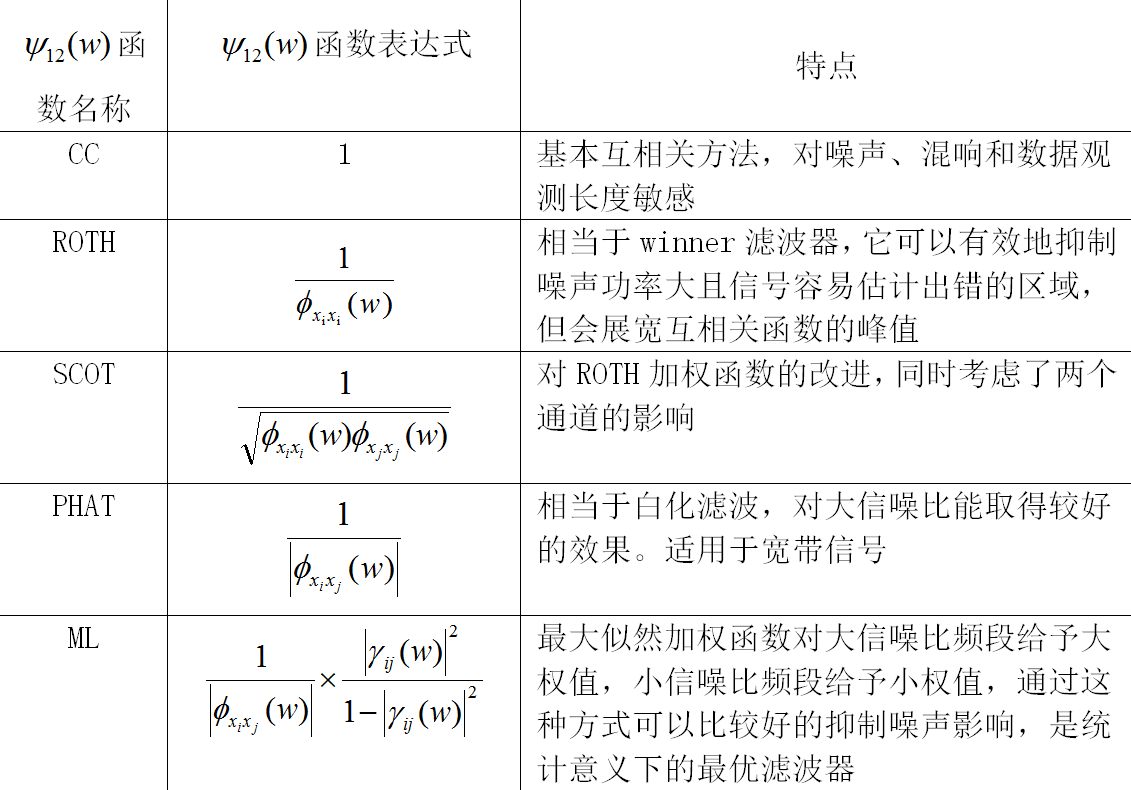
^{▲ 各種加權函數特性分析表格}

上表中， ${\phi }_{x_i{x}_i}\left(\omega \right)$、${\phi }_{x_j{x}_j}\left(\omega \right)$分別表示麥克風訊號$x_i\left(n\right)$ 、$x_j\left(n\right)$ 的自功率譜， ${\phi }_{x_i{x}_j}\left(\omega \right)$表示$x_i\left(n\right)$ 和$x_j\left(n\right)$ 的互功率譜， ${\left|{\gamma }_{ij}\left(\omega \right)\right|}^2$定義為如下形式[2]：

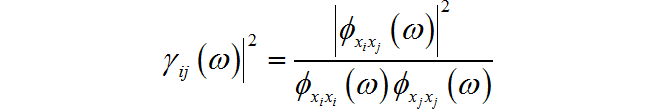
廣義互相關原理圖如圖C-7所示。

^{▲ 廣義互相關原理圖}

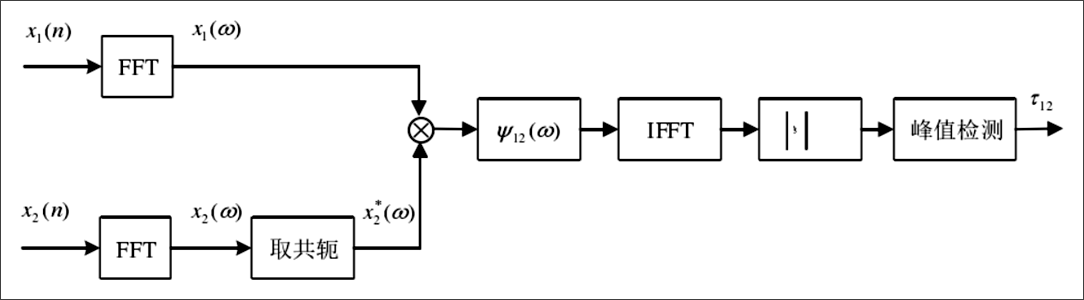
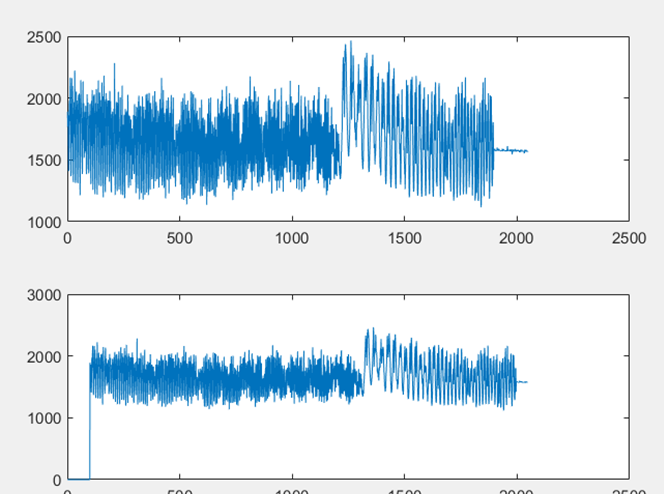
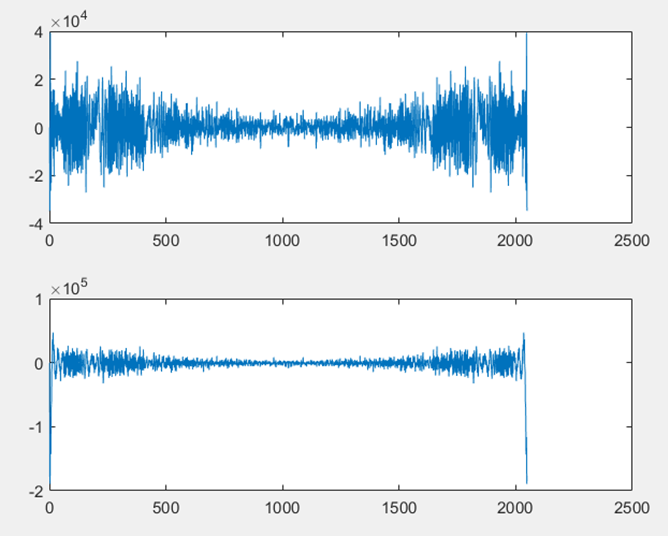
由於時間原因，本次備賽中我們只嘗試了GCC-PHAT和GCC-ML，其中只有GCC-PHAT試用成功了，GCC-ML還需要進一步研究。使用MATLAB對GCC-PHAT的效果進行模擬驗證，FM訊號和FM延時100點的訊號如圖C-8所示，兩者級聯FFT結果如圖C-8所示，在頻域相乘時，按照GCC-PHAT的方法要除以互功率譜的模，然後進行級聯IFFT，結果如圖C-9所示，最後取最大值點，MATLAB比較後最大值點為201。這和前面結果相同，也是符合理論結果的。

^{▲ 級聯FFT下FM訊號的100點延時的FM訊號波形}

^{▲ 級聯FFT下兩訊號級聯FFT變換波形}

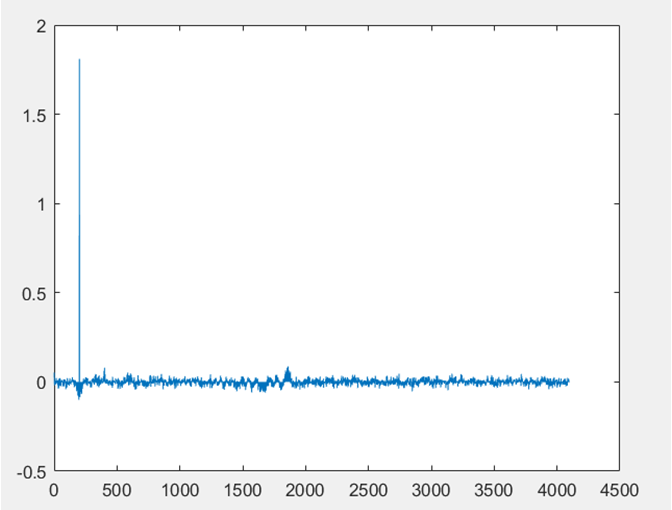
^{▲ 級聯FFT下兩訊號廣義互相關後的結果}

對比圖D-6和圖D-10，從級聯IFFT輸出的波形可以看出，相比於普通的互相關，廣義互相關的結果最大值以外的波形更加小和平緩，沒有很大的尖峰，效果更好，說明廣義互相關的確可以減小訊號失真的影響。

06.結論

對序列進行級聯FFT變換得到的結果和普通FFT變換得到的結果是完全一致的，模擬結果也說明使用級聯FFT代替FFT是沒有影響的，級聯FFT可以用於互相關運算。廣義互相關可以減小系統噪聲、混響等的影響，通過MATLAB模擬，比較普通互相關和廣義互相關的結果，從影象上可以看出廣義互相關的效果確實更好。

因此，在競賽中，結合TC264DA晶片的硬體FFT運算資源，級聯FFT可以大大減少運算時間，加快系統的響應速度；使用廣義互相關可以有效抑制噪聲、混響的干擾，提高互相關計算的準確度。

我們始終相信，訊號處理好，開環也能跑 。