「小和尚的遊戲」- -漢諾塔

相傳山上有個廟，廟裡有個小和尚和老和尚。一天小徒弟閒來無事，就去找老和尚，問有沒有什麼可以鍛鍊智力的遊戲，老和尚就給小和尚準備了三根柱子，說：首先第一根柱子上只有一個碗，你吧這個碗挪到第三個柱子上，小和尚很輕鬆的就完成了；然後老和尚又在第一根柱子上放了三個碗，而且這三個碗是按從小到大依次放，他這次要求小和尚把這三個碗從第一根柱子挪到第三根柱子上，但是挪動的過程中得保證小碗在大碗之上，且每次只能移動一個碗，小和尚思索片刻後，完成了目標；但是最後老和尚說我要是給你64個碗呢？ 小和尚陷入了思考。聰明的你知道怎麼做嘛？

漢諾塔（Hanoi Tower），又稱河內塔，源於印度一個古老傳說。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定，任何時候，在小圓盤上都不能放大圓盤，且在三根柱子之間一次只能移動一個圓盤。問應該如何操作？

1、挪一個盤子： （1步）

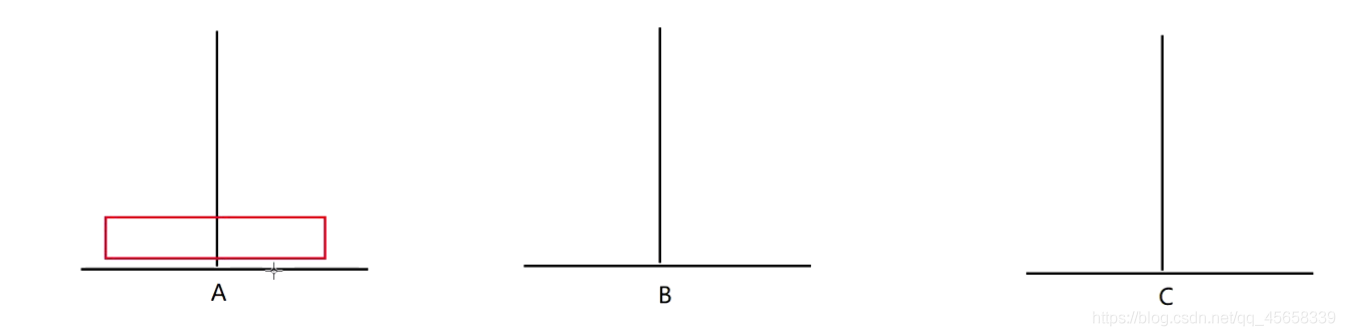
小朋友都知道的，當然是直接放過去就好了 A - - > C

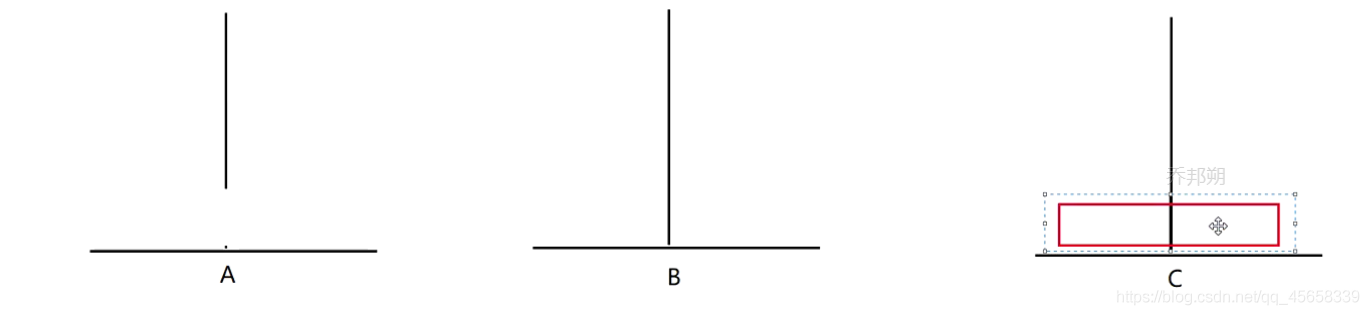
2、挪兩個盤子：（3步）

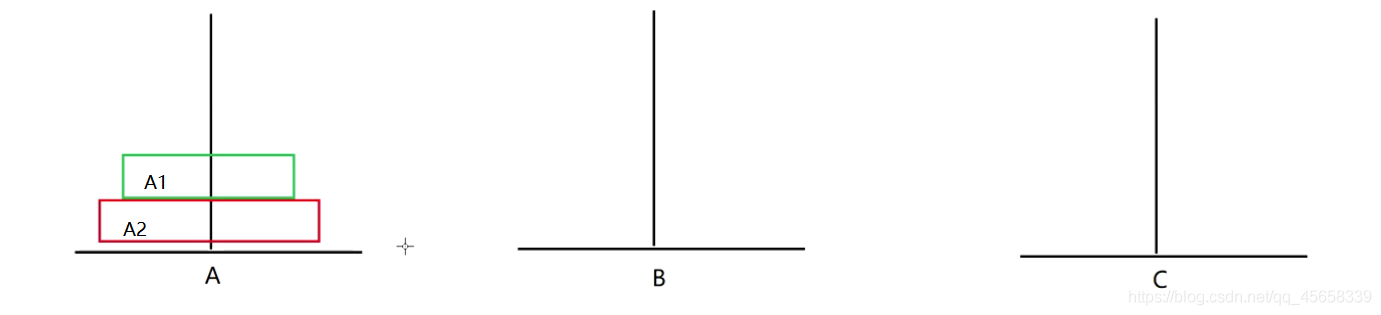
A1- - > B , A2 - - > C :

A1 - - > C :

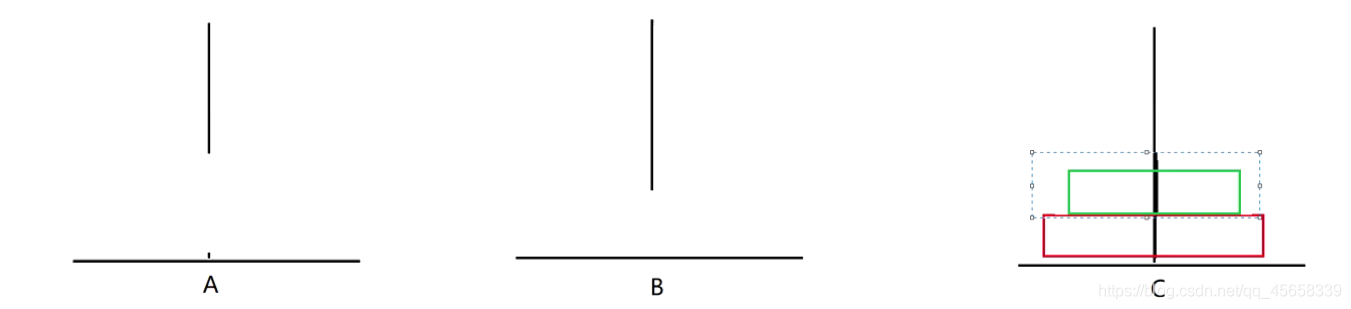
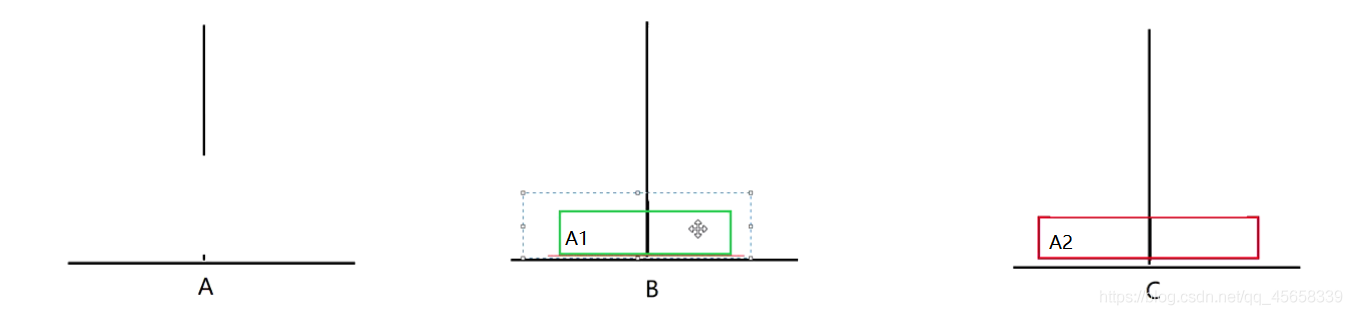
3、挪三個盤子： （7步）

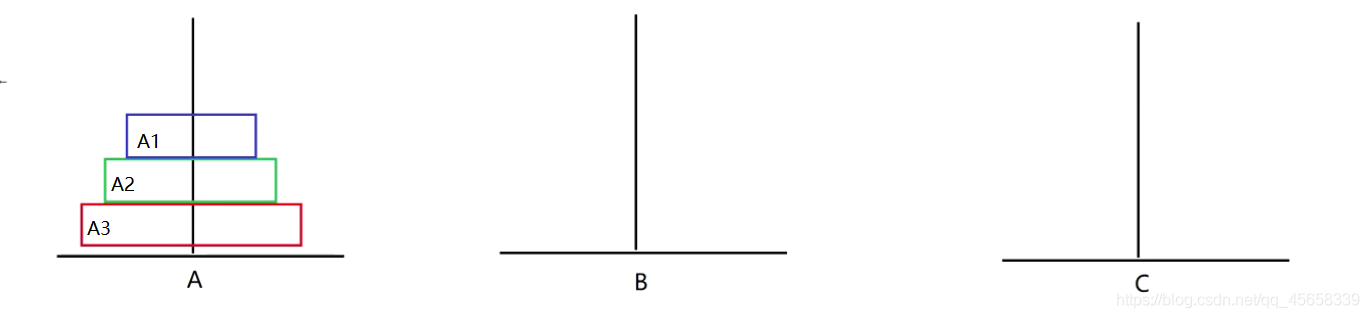
A1 - - > C , A2 - - > B :

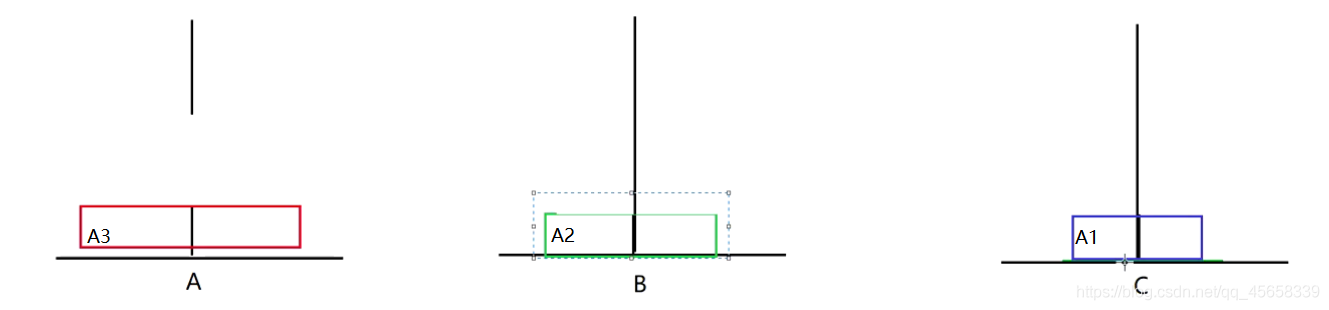
A1 - - > B , A3 - - > C :

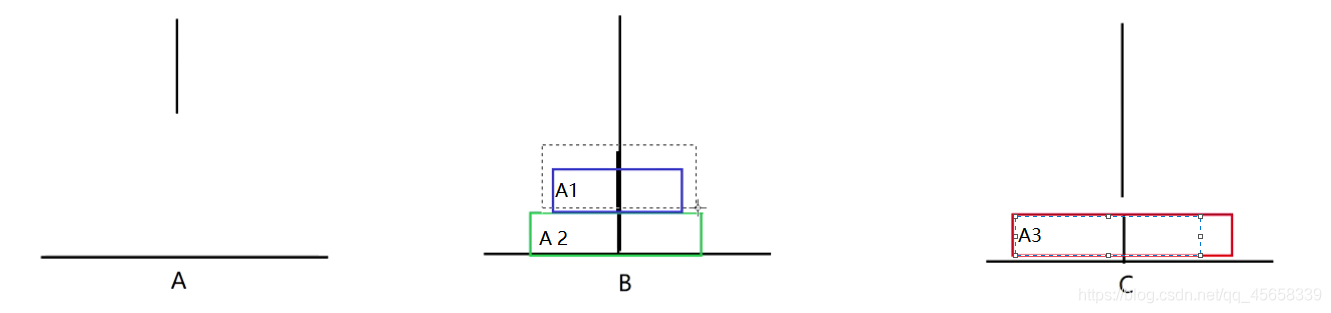
A1 - - > A , A2 - - > C , A1 - - > C

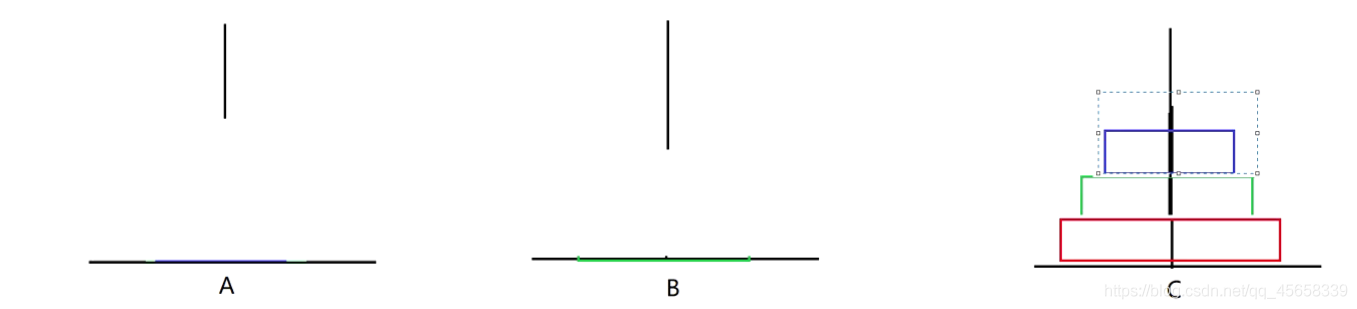
我們總結以上的規律 ：

挪一個盤子： 1步 = 2^1 - 1
挪兩個盤子： 3步 = 2^2 - 1
挪三個盤子： 7步 = 2^3 - 1
…
挪64個盤子： 2^64 - 1

我們簡單計算一下，計算機執行64個盤子得執行將近 300 年左右
所以我們簡單的輸出一下1、2、3個盤子的結果

package test24;

public class testDemo {
    public static void move (char pos1,char pos2) {
        System.out.print(pos1+" --> "+pos2+" ");//模仿滑鼠的移動
    }
    /**
     *
     * @param n       代表盤子的數目
     * @param pos1    代表第一根柱子  A
     * @param pos2    代表第二根柱子  B
     * @param pos3    代表第三根柱子  C
     */
    public static void HanoiTower (int n,char pos1,char pos2,char pos3) {  //n代表盤子的數目
        if(n == 1) {
            move(pos1,pos3);
        } else {
            HanoiTower(n-1,pos1,pos3,pos2);   // pos1 上的東西通過 pos3 傳到 pos2 上
            move(pos1,pos3);
            HanoiTower(n-1,pos2,pos1,pos3);
        }
    }
    public static void main(String[] args) {
        HanoiTower(1,'A','B','C');
        System.out.println();
        HanoiTower(2,'A','B','C');
        System.out.println();
        HanoiTower(3,'A','B','C');
        System.out.println();
    }

}

執行結果：

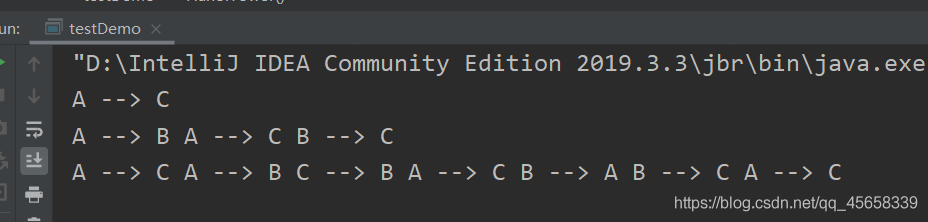
小夥伴想嘗試 64 個盤子的，可以自己試試哦！！！