本系列文章將於2021年整理出版。前驅教材：《演演算法競賽入門到進階》 清華大學出版社
網購：京東 噹噹   作者簽名書：點我
有建議請加QQ 群：567554289

  前言：
  可持久化線段樹（Persistent segment tree），或稱為函數式線段樹。中文網上把類似的演演算法思路稱為「主席樹」，「主席」並沒有確實的含義，而是詼諧的說法。NOIP選手黃嘉泰說：「這種求$k$大的方法（函數式線段樹）應該是我最早開始用的」（https://www.zhihu.com/question/31133885/answer/52670974）。黃嘉泰的拼音縮寫HJT，正好是古月(H)金帛(J)氵壽(T)的縮寫，所以被網友們稱為「主席」樹。
  函數語言程式設計（Functional programming），與物件導向程式設計（Object-oriented programming）、程式式程式設計（Procedural programming）並列。
  以下是正文。

  可持久化線段樹 是基本線段樹的一個簡單擴充套件，是使用函數語言程式設計思想的線段樹，它的特點是支援詢問歷史版本，並且利用歷史版本之間的共用資料來減少時間和空間消耗。
  可以用動畫做比喻來解釋它的思想：
  （1）一秒動畫由20幀左右的靜態畫面連續播放而成，每2個相鄰畫面之間差別很小；
  （2）如果用計算機來製作動畫，為節省空間，讓每一幀畫面只記錄與前一幀的不同處；
  （3）如何生成完整的每一幀畫面？從第1幀畫面開始播放，後面的每一幀用自己的不同處替換前一幀的相同位置，並填補上相同的畫面，就生成了新的畫面。
  （4）兩幀不同時間的畫面做「減法」，得到一個新的畫面，這個新畫面反映了兩個時間點之間的資訊。
  與動畫類似，可持久化線段樹的基本思路是：
  （1）有多棵線段樹（每棵線段樹是一幀畫面）；
  （2）相鄰兩棵線段樹之間差別很小，所以每棵線段樹在物理上只需要儲存與前一棵的不同處，使用的時候再填補並生成一棵完整的線段樹；
  （3）任意兩棵線段樹能「相減」得到一棵新線段樹，它往往包含了題目需要的解。
  可持久化線段樹的基本特點是「多棵線段樹」，根據具體情況，每棵線段樹可以表示不同的含義。例如在「區間第$k$大問題」中，第$i$棵樹是區間$[1,i]$的線段樹；在「hdu 4348區間更新問題」中，第$i$棵樹是第$t$時間的狀態。
  需要建多少棵樹？題目給定包含為$n$個元素的序列，每次用一個新元素建一棵線段樹，共n棵線段樹。
  每棵樹有多少結點？線段樹的葉子結點記錄（或者代表）了元素，如果元素沒有重複，葉子節點就設為$n$個；如果元素有重複，根據情況，葉子結點可以設為$n$個（例題hdu 5919），也可以設為不重複元素的數量（例題洛谷P3834）。
  可持久化線段樹用到的技術包括：字首和思想 + 共用點 + 離散化 + 權值線段樹（可以相減） + 動態開點。
  下面用經典問題「區間第$k$大」來介紹可持久化線段樹的思想，並給出模板，然後介紹幾個典型例題。

1. 「區間第k大」問題

---

主席樹 洛谷 P3834
題目描述：給定n個整數構成的序列a，隊指定的閉區間[L, R]，查詢區間內的第k小值。
輸入：第一行包含2個整數，分別表示序列長度n喝查詢個數m。第二行包含n個整數，第i個整數表示序列的第i個元素ai。下面有m行，每行包含3個整數L，R，k，表示查詢區間[L, R]內的第k小值。
輸出：對每個詢問，輸出一行一個整數表示答案。
資料規模：1 ≤ n, m ≤ 2*$10^5$, |ai| ≤ $10^9$, 1 ≤ L ≤ R ≤ n，1 ≤ k ≤ R-L+1

---

  如果簡單地用暴力法查詢，可以先對區間[L, R]內的元素排序，然後定位到第$k$小的元素，複雜度$O(nlogn)$。$m$次查詢的總複雜度是$O(mnlogn)$。
  能否用線段樹求解？線段樹特別適合處理區間問題，例如做區間和、區間最值的修改和查詢，一次操作的複雜度是$O(logn)$的。在「線段樹」這一節曾指出，這些問題的特徵是大區間的解可以從小區間的解合併而來。然而區間第$k$小這種問題，並不滿足這種特徵，無法直接用線段樹。
  本題仍可以用線段樹，但不是在一個線段樹上操作，而是建立很多線段樹，其關鍵是：兩個線段樹相減得到新線段樹，新線段樹對應了新區間的解。
  下面逐步推出可持久化線段樹的解題思路。
  以序列{245, 112, 45322, 98988}為例，序列長度$n$ = 4。
  （1）離散化。把序列離散化為{2, 1, 4, 3}，離散化後的元素值是1 ~ $n$，離散化不影響查詢第$k$小。做離散化操作的原因後文有解釋。如果有重複元素，見後面的解釋。

   （2）先思考如何用線段樹查詢區間$[1,i]$的第$k$小。即查詢的區間是從1個元素到第i個元素。
  對一個確定的$i$，首先建立一棵包含區間$[1,i]$內所有元素的線段樹，然後在這棵樹上查詢第$k$小，複雜度是$O(logn)$的。
  對每個$i$，都建立一棵區間$[1,i]$的線段樹，共$n$棵樹。查詢每個$[1,i]$區間的第$k$小，都是$O(logn)$的。
  下面的圖，分別是區間[1, 1]、[1, 2]、[1, 3]、[1, 4]的線段樹，為了統一，把4個線段樹都設計成一樣大，即可容納$n$ = 4個元素的線段樹。圓圈內部的數位，表示這個區間內有多少個元素，以及它們在哪些子樹上。把圓圈內的值稱為結點的權值，整棵樹是一棵權值線段樹。

圖1. 4棵線段樹

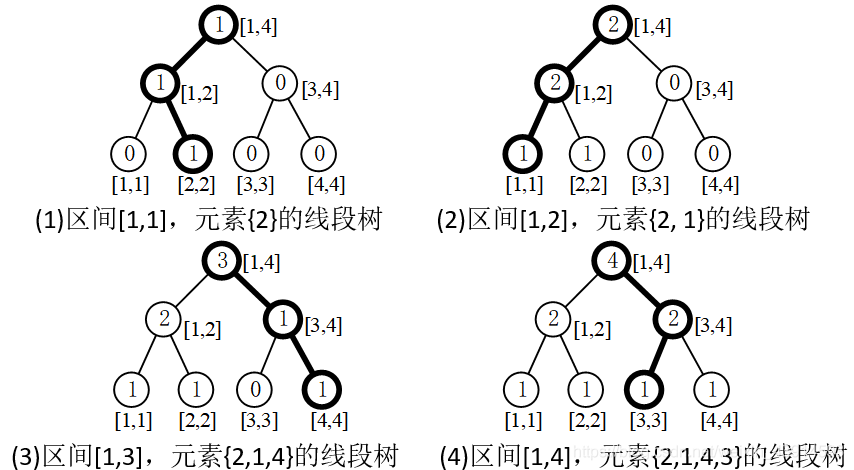
  可以觀察到，每棵樹與上一棵樹只有部分結點不同，就是粗線上的結點，它們是從根到葉子的一條鏈。
  葉子結點的序號實際上就是元素的值，例如葉子[1, 1]表示元素{1}，葉子[2, 2]表示元素{2}，等等。這也是對原序列進行離散化的原因，離散化之後，元素1~$n$對應了$n$個葉子。一個結點的左子樹上儲存了較小的元素，右子樹上儲存較大的元素。
  如何查詢區間[1, i]的第k小？例如查詢區間[1, 3]的第3小，圖(3)是區間[1, 3]的線段樹，先查根結點，等於3，說明區間內有3個數；它的左子結點等於2，右子結點等於1，說明第3小數在右子樹上；最後確定第3小的數是最後一個葉子，即數位4。查詢路徑是[1, 4]->[3, 4]->[4, 4]。
  （3）查詢區間[L, R]的第$k$小。
   如果能得到區間[L, R]的線段樹，就能高效率地查詢出第$k$小。根據字首和的思想，區間[L, R]包含的元素等於區間$[1,R]$減去區間$[1,L-1]$。把字首和思想用於線段樹的減法，線段樹的減法，是在兩棵結構完全的樹上，把所有對應結點的權值相減。線段樹$R$減去線段樹$L-1$，就得到了區間$[L,R]$的線段樹。
  例如區間[2, 4]的線段樹，等於把第4個線段樹與第1個線段樹相減（對應圓圈內的數位相減），得到下圖的線段樹：

圖2. 區間[2, 4]的線段樹

  觀察圖中的葉子結點，只有1、3、4這幾個葉子結點有值，正好對應區間[2, 4]的元素{1, 3, 4}。
   查詢區間[2, 4]的第$k$小，方法與前面查詢區間$[1,i]$的第$k$小一樣。
   時間複雜度分析。2個線段樹相減，如果對每個結點做減法，結點數量是$O(n)$的，複雜度很高。但是實際上只需要對查詢路徑上的結點（以及它們的左右子結點）做減法即可，這些結點只有$O(logn)$個，所以做一次「線段樹減法 + 查詢第k小」操作，總複雜度是$O(logn)$的。
   （4）儲存空間。上述演演算法的時間複雜度很好，但是需要的儲存空間非常大，建立n棵線段樹，每棵樹的空間是$O(n)$，共需$O(n^2)$的空間，$n=10^5$時，$n^2$ = 10G。
   如何減少儲存空間？觀察這$n$棵線段樹，相鄰的2棵線段樹，絕大部分結點的值是一樣的，只有與新加入元素有關的那部分不同，這部分是從根結點到葉子結點的一條路徑，路徑上共有$O(logn)$個結點，只需要儲存這部分結點就夠了。$n$棵線段樹的總空間複雜度減少到$O(nlogn)$。
   下圖演示了建第1棵樹的過程。先建一棵原始空樹，它是一棵完整的線段樹；然後建第1棵樹，第1棵樹只在原始空樹的基礎上修改了圖(1)中的3個結點，那麼只新建這3個結點即可，然後讓這3個結點指向原始空樹上其他的子結點，得到圖(2)的一棵樹，這棵樹在邏輯上是完整的。

圖3 建初始空樹和第1棵樹

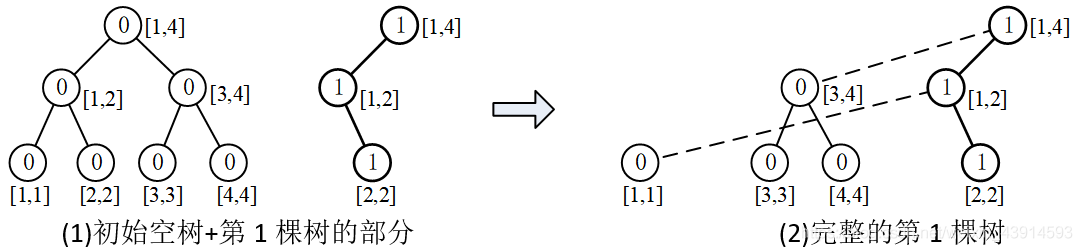
  建其他樹時，每次也只建與前一棵樹不同的$O(logn)$個結點，並把新建的結點指向前一棵樹的子結點，從而在邏輯上仍保持為一棵完整的樹。
   建樹的結果是：共建立了$n$棵線段樹，每棵樹在物理上只有$O(logn)$個結點，但是在邏輯上是一棵完整的線段樹。在這些「殘缺」的線段樹上操作，與在「完整」的線段樹上操作相比，效果是一樣的。
  以上是演演算法的基本內容，建樹的時間複雜度是$O(nlogn)$，m次查詢的時間複雜度是$O(mlogn)$。
   編碼的時候，有3個重要的細節：
   （1）如何定位每棵線段樹。需要建立$n$棵線段樹，這$n$棵線段樹需要方便地定位到，以計算線段樹的減法。可以定義一個$root[]$陣列，$root[i]$記錄第$i$棵線段樹的根結點編號。
  （2）初始空樹。一般情況下，並不需要真的建一棵初始空樹，而是直接從建第1棵樹開始。因為空樹的結點權值都是0，空樹與其他線段樹做減法是多餘的。在沒有初始空樹的情況下，建立的$n$棵線段樹不僅在物理上都是「殘缺」的，在邏輯上也不一定完整；後面建立的線段樹，形態逐漸變得完整。在「殘缺」的線段樹上做查詢，結果仍然是正確的，因為那些在邏輯上也沒有的結點不需要納入計算，可以看成權值為0。不用寫建初始空樹的程式碼，能節省一些編碼時間。
  （3）原始序列中有重複的元素。重複的數位仍需要統計，例如序列{1, 2, 2, 3, 4}，區間[1, 5]的第3小數位是2，不是3。編碼時對n個元素離散化，並用$unique()$去重得到$size$個不同的數位。每個線段樹的葉子結點有$size$個，用$update()$建新的線段樹時，若遇到重複的元素，累加對應葉子結點的權值以及上層結點的權值即可。用$update()$建的線段樹總共仍有$n$個，不是$size$個。（有網友說「update函數好像會被杭電掛掉」，可以改個函數名）
  下面的程式碼實現了上述演演算法。其中新建線段樹的每個結點，是動態開點。其中的查詢函數$query()$，可以看成在一棵邏輯上完整的線段樹上做查詢操作。

//洛谷P3834程式碼, 改寫自：https://www.luogu.com.cn/problem/solution/P3834
#include <bits/stdc++.h>
using namespace std ;

const int MAXN = 200010;
int cnt = 0;        //用cnt標記可以使用的新結點
int a[MAXN], b[MAXN], root[MAXN]; 
                    //a[]是原陣列,b[]是排序後陣列，root[i]記錄第i棵線段樹的根節點編號

struct{             //定義結點
int L, R, sum;  //L左兒子, R右兒子，sum[i]是結點i的權值（即圖中圓圈內的數位）
}tree[MAXN<<5];     //  <<4是乘16倍，不夠用   

int build(int pl, int pr){        //初始化一棵空樹
    int rt = ++ cnt;              //cnt為當前節點編號
    tree[rt].sum = 0;
    int mid=(pl+pr)>>1;
    if (pl < pr){
        tree[rt].L = build(pl, mid);
        tree[rt].R = build(mid+1, pr);
    }
    return rt;  //返回當前節點的編號
}
int update(int pre, int pl, int pr, int x){   //建一棵只有logn個結點的新線段樹
    int rt = ++cnt;          //新的結點，下面動態開點
    tree[rt].L = tree[pre].L;//該結點的左右兒子初始化為前一棵樹相同位置結點的左右兒子
    tree[rt].R = tree[pre].R; 
    tree[rt].sum = tree[pre].sum + 1;  //插了1個數，在前一棵樹的相同結點加1
    int mid = (pl+pr)>>1;
    if (pl < pr){           //從根結點往下建logn個結點
        if (x <= mid)       //x出現在左子樹，修改左子樹 
            tree[rt].L = update(tree[pre].L, pl, mid, x);
        else                //x出現在右子樹，修改右子樹
            tree[rt].R = update(tree[pre].R, mid+1, pr, x);
    }
    return rt;              //返回當前分配使用的新結點的編號
}

int query(int u, int v, int pl, int pr, int k){    //查詢區間[u,v]第k小
    if (pl == pr) return pl;  //到達葉子結點，找到第k小，pl是節點編號，答案是b[pl] 
    int x = tree[tree[v].L].sum - tree[tree[u].L].sum;   //線段樹相減
    int mid = (pl+pr)>>1;
    if (x >= k)     //左兒子數位大於等於k時，說明第k小的數位在左子樹
        return query(tree[u].L, tree[v].L, pl, mid, k);
    else            //否則在右子樹找第k-x小的數位 
        return query(tree[u].R, tree[v].R, mid+1, pr, k-x);
}

int main(){
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++){
        scanf("%d", &a[i]);
        b[i] = a[i];
    }
    sort(b+1, b+1+n);    //對b排序
    int size = unique(b+1, b+1+n)-b-1; //size等於b陣列中不重複的數位的個數
    //root[0] = buildtree(1, size);   //初始化一棵包含size個元素的空樹，實際上無必要
    for (int i = 1; i <= n; i ++){     //建n棵線段樹
        int x = lower_bound(b+1, b+1+size, a[i]) - b;
                                  //找等於a[i]的b[x]。x是離散化後a[i]對應的值
        root[i] = update(root[i-1], 1, size, x);  
                                  //建第i棵線段樹，root[i]是第i棵線段樹的根結點
    }
    while (m--){
        int x, y, k;
        scanf("%d%d%d", &x, &y, &k);
        int t = query(root[x-1], root[y], 1, size, k); 
                          //第y棵線段樹減第x-1棵線段樹，就是區間[x,y]的線段樹
        printf("%d\n", b[t]);
    }
    return 0;
}

   需要分配的空間是$O(nlogn)$，具體是多少？線上段樹這一節曾指出，一棵線段樹需要分配$4n$個結點，那麼總空間約為$nlog(4n)$，題目給定$n=200000$，$log(4n)\approx 20$，程式碼中定義的$tree[MAXN<<5]$夠用。
   區間第$k$大問題的另一種解法是莫隊演演算法，見上一節「分塊與莫隊演演算法」。

2. 區間內小於等於k的數位有多少

---

Super Mario hdu 4417
題目描述：給定一個整數序列，有n個數。有m個詢問，詢問區間[L,R]內小於k的整數有多少個。
輸入：第一行是整數T，表示測試用例個數。對每個測試，第一行是整數n,m。下一行是n個整數a1, a2, …, an，後面有m行，每行有3個整數L、R、k。
輸出：對每個測試用例，輸出m行，每行是一個詢問的答案。
資料範圍：1 ≤ n, m ≤ 105, 0 ≤ ai ≤ $10^5$, 1 ≤ L ≤ R ≤ n，1 ≤ ai, k ≤ $10^9$

---

  「區間內小於等於$k$的數位有多少」問題與「區間第$k$小」問題很相似。
  （1）$update()$函數，建$n$棵線段樹，與例題「洛谷P3834」的程式碼一樣。線段樹的每個結點的權值是這棵子樹下葉子結點的權值之和。
  （2）$query()$函數，統計區間$[L,R]$內小於等於$k$的數位有多少個。首先用線段樹減法（線段樹$R$減去線段樹$L-1$）得到區間$[L,R]$的線段樹，然後統計這棵樹上比$k$小的數位即可，統計方法就是標準的線段樹「區間和」查詢。例如圖2，它是{1, 3, 4}的線段樹，如果求小於等於$k$=3的數位有多少，答案就是求這棵線段樹的區間[1, 3]的區間和，它等於[1, 2]區間和加上[3, 3]區間和。同樣，這裡做線段樹的減法，並不需要把每個結點相減，只需要對查詢路徑上的結點做減法（即結點[3, 3]和結點[1, 2]），只涉及到$O(logn)$個結點。

3. 區間內有多少不同的數位

---

Sequence II hdu 5919
題目描述：一個整數序列，有n個數A[1], A[2], …, A[n]。做m次詢問，第i個詢問，給定兩個整數Li、Ri，表示一個區間，區間內是一個子序列，其中不同的整數有ki個，輸出第ki/2個整數在這個子序列中第一次出現的位置。
輸入：第一行是整數T，表示測試用例個數。對每個測試，第一行是2個整數n和m，下面一行是n個整數，表示序列。後面m行，每行有兩個整數Li、Ri。
輸出：對每個測試，輸出一行，包括m個回答。
資料範圍：1 ≤ n, m ≤ 2*$10^5$, 0 ≤ A[i] ≤ $10^5$

---

   首先求區間內有多少個不同的數位。若按前面建主席樹的方法，第$i$棵主席樹記錄區間$[1,i]$內的數位情況，如何定義葉子結點的權值？考慮2種方案：
  （1）葉子結點的權值是這個數位出現的次數。那麼查詢區間$[L,R]$內不同數位個數時，用線段樹$R$減去線段樹$L-1$，得到區間$[L,R]$的線段樹，此時每個葉子結點的權值是這個數位在區間內$[L,R]$出現的次數。在這棵線段樹上，無法以$O(logn)$的複雜度計算不同的數位個數。
  （2）葉子結點的權值等於1，表示這個數位在區間$[1,i]$出現過；等於0，表示沒有出現過。這樣做可以去重，但是無法用線段樹減法來計算區間的不同數位個數。例如，區間$[1,L-1]$內出現某個數位，區間$[L,R]$內再次出現這個數位，它們對應的葉子結點權值都是1；對線段樹$R$和$L-1$做減法後，得到$[L,R]$區間的線段樹，這個葉子結點的權值是0，表示這個數位不存在，而區間$[L,R]$內其實是有這個數位的。
  這題仍可以用主席樹，但是需要使用新的技巧：倒序建立這$n$棵線段樹。
  （1）每棵線段樹的葉子結點有$n$個。這與例題「洛谷P3834」的線段樹不同。第$i$個葉子結點記錄第$i$個元素是否出現。
  （2）按倒序建立線段樹。一個元素建立一棵線段樹，用第$n$個元素$A[n]$建立第1個線段樹，用第$n-1$個元素$A[n-1]$建立第2個線段樹…，共有$n$棵線段樹。用元素$A[n]$建立第1棵線段樹時，第n個葉子結點的權值是1；…；建立第$i-1$棵線段樹時，若$A[i-1]$在區間$[i,n]$中曾出現過，將第$i$個葉子結點的權值置為0，然後把第$i-1$個葉子結點權值記為1。這個操作把重複的元素從第$i-1$個線段樹中剔除，只在第1次出現的葉子結點位置記錄權值。如何程式設計實現？可以定義$mp[]$陣列，$mp[A[i]]=i$，表示元素$A[i]$在第i個線段樹的第$i$個葉子結點出現；建第$k$個線段樹時，若$mp[A[k]]>0$，說明$A[k]$這個元素曾出現過，先把第$k$個線段樹的第$mp[A[k]]$個葉子結點權值置為0，然後把第$k$個葉子結點權值置為1。
  （3）查詢區間$[L,R]$內不同數位個數。第$L$棵線段樹，只記錄了$A[L]$ ~ $A[n]$區間內不同數位的情況，而不包括$A[1]$ ~ $A[L-1]$，那麼只需要在第$L$棵線段樹上，按標準的區間查詢操作計算$[1,R]$的區間和，就是答案。
  題目要求輸出區間[$L,R]$內第$k/2$個整數在這個區間中第一次出現的位置，由於第$L$棵線段樹記錄的就是$A[L]$ ~ $A[n$]第1次出現的位置，那麼只需要在這棵線段樹上查詢$[1,R]$的第$k/2$個葉子結點即可。

4. 區間更新

---

To the moon hdu 4348 區間更新
題目描述：給定n個整數A[1], A[2], …, A[n]，執行m個操作，有以下幾種操作：

1. C L R d 區間[L, R]每個A[i]加上d，時間$t$加1，注意只有這個操作才會改變$t$，第1個操作$t$=1。
2. Q L R 查詢區間和
3. H L R t 查詢時間t的歷史區間和
4. B t 返回時間t，t以後的操作全部清空
   1 ≤ n, m ≤ 105, |A[i]| ≤ $10^9$, 1 ≤ L ≤ R ≤ n，|d|≤ $10^4$

---

  若沒有時間$t$，只需要建一棵線段樹，就是標準的線段樹模板題。加上時間點$t$後，每個時間點建一棵線段樹，這正符合主席樹的標準應用，按標準的主席樹編碼即可。

習題

  區間第k大：hdu2665
  可持久化陣列：洛谷 P3919
  主席樹專題訓練：https://www.cnblogs.com/HDUjackyan/p/9069311.html
  帶修改的主席樹：ZOJ 2112 Dynamic Rankings