經典例題

網上有什麼十大經典例題，但無非3種操作：矩陣的基礎運算（例一+加減乘+階乘），找輔助矩陣解題，與其他知識點結合用作矩陣加速（降複雜度，一般降成logn）

操作一：單單矩陣的基礎操作

給定n個點，m個操作，構造O(m+n)的演演算法輸出m個操作後各點的位置。操作有平移、縮放、翻轉和旋轉，置換

有些模擬題也會用到矩陣的基礎操作，但很少這種矩陣運算。

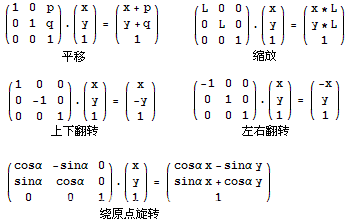
在這裡插入圖片描述

高階操作：反覆置換，共軛轉置，酉矩陣，（半）正定矩陣等等
上述定義

操作二：階乘

給定矩陣A，請快速計算出A^n（n個A相乘）的結果，輸出的每個數都mod p。
給定一個有向圖，問從A點恰好走k步（允許重複經過邊）到達B點的方案數mod p的值

變式：用1 x 2的多米諾骨牌填滿M x N的矩形有多少種方案，M<=5，N<2^31，輸出答案mod p的結果。

這種題本質上還是一樣的，利用狀態轉換，畫個有向圖，然後跟上面的問題一樣了。
例題：規定寬度為4，給定長度為n，求用12和21的瓷磚，將其完全鋪滿能有多少種方法。（連結一，還有杜教BM）
連結二，有推導過程

例如：二階矩陣如下

const int N=2;
typedef struct matrix{	int a[N][N];	}mt;
mt muti(mt x,mt y){
	mt z;	memset(z.a,0,sizeof(z.a));
	for(int i=0;i<N;i++)
		for(int j=0;j<N;j++)
			for(int k=0;k<N;k++)
				z.a[i][j]=(z.a[i][j]+x.a[i][j]*y.a[j][k]%mod)%mod;
	return z;
}
mt qpow(mt x,int k){
	mt y;	memset(y.a,0,sizeof(y.a));
	for(int i=0;i<N;i++)	y.a[i][i]=1;
	while(k){
		if(k&1)	y=muti(y,x);
		k>>=1;	x=muti(x,x);
	}
	return y;
}

一個nm的矩陣乘一個mp的矩陣會得到一個n*p的矩陣

//n*m的矩陣乘 m*p的矩陣 
typedef struct matrix{	int n,m,a[maxn][maxn];	}mt;
mt muti(mt x,mt y,int n,int m,int p){
	mt z;	memset(z.a,0,sizeof(z.a));	
	for(int i=0;i<x.m;i++)			//m
		for(int j=0;j<y.n;j++)		//p
			for(int k=0;k<x.n;k++)	//n
				z.a[i][j]=(z.a[i][j]+x.a[i][j]*y.a[j][k]%mod)%mod;
	return z;
}

操作三：找輔助矩陣
1、專業點說是：用矩陣乘法優化的線性齊次遞推公式求值。
2、線性關係推不出的話，可以嘗試杜教BM，暴力推出係數，如果推不出，應該不是線性關係。（小編還不會杜教BM）
3、這類題有時也可以用二分，dfs+剪枝，dp等等做。

題型：

1、給定n和p，求第n個Fibonacci數mod p的值，n不超過2^31
普通的有兩種方法：詳解

往往是變式題，要自己找輔助矩陣
對於f(n)=af(n-1)+bf(n-2)這種遞推公式。有一種方法是提特徵根方程：講解
但上面的方法對於特徵根是無理數時，無效，無特徵根時又要考慮其是否有周期性。而用矩陣乘法寫的普適性更強。

找輔助矩陣練習： 
一：求Fibonacci前n項和
矩陣遞推式；
Sn = 1 * Sn-1 + 1 * fn + 0 * fn-1;
fn+1 = 0 * Sn-1 + 1 * fn + 1 * fn-1;
fn = 0 * Sn-1 + 1 * fn + 0 * fn-1;
{1 1 0}
{0 1 1}
{0 1 0}

二：求Tn= ∑k*fk mod m；

    原式
    f[i] = f[i-1]+f[i-2]
    T[n] = f[1]+f[2]*2+f[3]*3+...+f[n]*n

    令
        S[n] = f[1]+f[2]+f[3]+...+f[n]
    n*S[n] = n*f[1]+n*f[2]+n*f[3]+...+n*f[n]
    設
    --> P[n] = n*S[n]-T[n]
    --> P[n] = (n-1)*f[1]+(n-2)*f[2]+...+(n-n)*f[n]
    因為
    --> P[n-1] = (n-1)*S[n]-T[n-1]
    --> P[n-1] = (n-2)*f[1]+(n-3)*f[2]+...+(n-1-(n-1))*f[n-1]
    且
    --> S[n-1] = f[1]+f[2]+f[3]+....+f[n-1]
    所以
    P[n]=P[n-1]+S[n-1]
    
    P[n]=1*P[n-1]+1*S[n-1]+0*f[n]+0*f[n-1];
    S[n]=0*P[n-1]+1*S[n-1]+1*f[n]+0*f[n-1];
  f[n+1]=0*P[n-1]+0*S[n-1]+1*f[n]+1*f[n-1];
    f[n]=0*P[n-1]+0*S[n-1]+1*f[n]+0*f[n-1];
	    
 	P[i] S[i] f[i] f[i-1]
    
    {1 1 0 0} 
    {0 1 1 0} 
    {0 0 1 1} 
    {0 0 1 0} 
    
    最後 T[n] = n*S[n]-P[n];

2、二分遞迴或找輔助矩陣
題目大意：給定矩陣A，求A + A^2 + A^3 + … + A^k的結果（兩個矩陣相加就是對應位置分別相加）。輸出的資料mod m。k<=10^9。
一共有4種解法，歸於兩大種，年代已久，連結已失（其實是懶得再找了）。

3、求下列函數的整數部分（含根號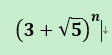）在這裡插入圖片描述

推導過程：矩陣快速冪+共軛複數

然後是通用公式，求整數部分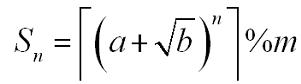在這裡插入圖片描述
注意這類都有一個大前提才能共軛構造，見推導過程

總結

還在刷題，這篇還在更新，沒什麼好總結的。

矩陣乘法回顧

目錄

經典例題

總結