本文的主要線路是證明取樣定理中的頻域變換式。

其中知識框架如下：

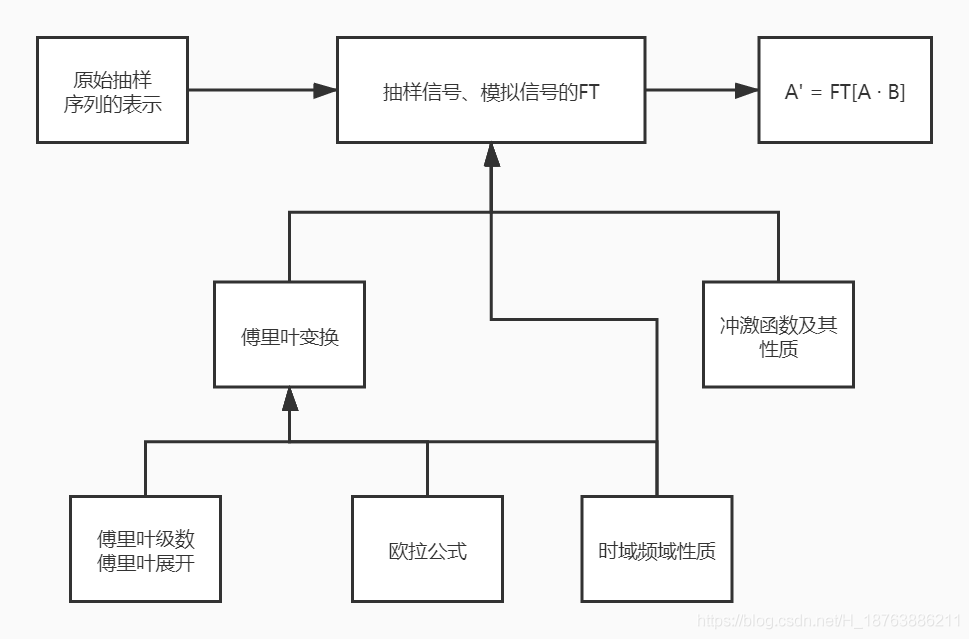
以下將從按照拓撲序進行相關模組的設計

傅立葉級數與傅立葉展開

傅立葉級數

傅立葉級數類似於泰勒級數，是一種特殊的描述函數的方式。

傅立葉級數的定義為：

$$\begin{gathered} f(x)=a_0+\sum _{n=1}^{+\infty }(a_n\cos (nwx)+b_n\sin (nwx)) \\ f(x)=\sum _{n=0}^{+\infty }(a_n\cos (nwx)+b_n\sin (nwx)),b_0=0 \end{gathered}$$

它能夠描述函數的原理為：傅立葉認為所有周期函數都可以展開成為若干三角函數的求和。

上面的原理我們可以描述為以下的式子：

$$\begin{gathered} f(x)=\sum _{i=1}^{+\infty }{k}_i\sin (w_{i}x+b_i) \\ =\sum _{i=1}^{+\infty }{k}_i(\sin (w_{i}x)\cos (b_i)+\cos (w_{i}x)\sin (b_i)) \\ =\sum _{i=1}^{+\infty }{k}_i\cos (b_i)\sin (w_{i}x)+k_i\sin (b_i)\cos (w_{i}x) \\ =\sum _{i=1}^{+\infty }{a}_i\sin (w_{i}x)+b_i\cos (w_{i}x) \end{gathered}$$

這個是不是長得很像上面的那個式子啊 ^ _ ^，唯一不同的就是上面那個式子中$w_i$取的都是整數, 而不是像下面這樣隨便取值 ( 隨便取值這個叫做傅立葉變換, 後面會有的 )

傅立葉展開

那傅立葉展開是啥? 傅立葉展開就是把一個函數的傅立葉級數給求出來. 可以類比泰勒展開是求泰勒級數一樣, 傅立葉展開的目的就是求傅立葉級數.

這裡需要用到的知識有三角函數的正交性.

具體來說的話就是對於在集合 { 1 , sin ⁡ x , cos ⁡ x , sin ⁡ 2 x , cos ⁡ 2 x , . . . , sin ⁡ n x , cos ⁡ n x } \{1, \sin x, \cos x, \sin 2x, \cos 2x, ... , \sin nx, \cos nx\} {1,sinx,cosx,sin2x,cos2x,...,sinnx,cosnx}中任取兩個函數A(x), B(x). 則滿足以下性質:

$${\int }_{-\pi }^{\pi }A(x)B(x)dx=\{\begin{array}{ll}0,& A(x)\ne B(x)\\ \pi ,& A(x)=B(x)\ne 1\\ 2\pi ,& A(x)=B(x)=1\end{array}$$

於是就有了求解上面的$a_n,b_n$的方法:

$$\begin{gathered} a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f(x)dx \\ {a}_n=\frac{2}{2\pi }{\int }_{-\pi }^{\pi }f(x)\cos (nx)dx \\ {b}_n=\frac{2}{2\pi }{\int }_{-\pi }^{\pi }f(x)\sin (nx)dx \end{gathered}$$

這裡需要注意一個問題, 就是關於傅立葉級數上面的$a_0$的表示方法, 這個有等價形式, 詳情請看: 傅立葉級數

然後這裡就完成了傅立葉級數和傅立葉展開的簡單回顧.

尤拉公式

先上尤拉公式的公式

$$e^{ix}=\cos (x)+i\sin (x)$$

這個公式的證明是尤拉完成的, 但是可以有一些有趣的理解:

$-x=x\ast i^2=x\ast -1$如果放在數軸上看, 是不是可以把-x看成x逆時針旋轉了180°, 那麼兩個$i$能讓它轉180°, 一個$i$自然可以讓它轉 90°吧? 所以啊, 這個$i$就可以看成是一個90°旋轉角.

於是任何一個二維平面上的點都可以表示成 $|A|e^{\rho i}$的形式. 同樣一個點經過了$x\ast 90°$的旋轉, 是不是可以表示成這個點原先的位置乘了$e^{xi}$

除此之外, 這個復指數函數還滿足普通指數函數滿足的一些性質.

$$\begin{gathered} {\rho }_1{e}^{ai}\cdot {\rho }_2{e}^{bi}={\rho }_1{\rho }_2{e}^{(a+b)i} \\ {e}^{-ix}=\cos (x)-i\sin (x) \end{gathered}$$

剩下的一些其他性質可以看複變函數相關的資料.

時域頻域關係

音符舉例

先來一個看起來很形象的例子: 一個音符.

時域中的樣子可能是這樣的

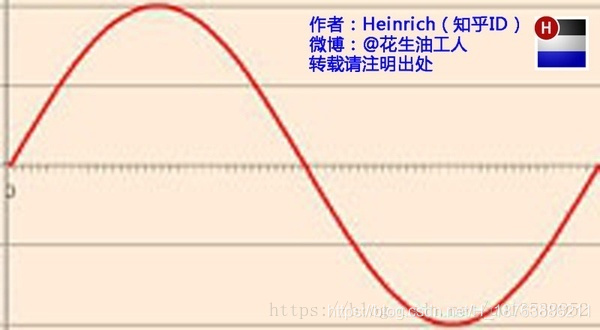
其中橫軸是時間, 縱軸是你接收到的模擬訊號的強度

那麼它在頻域的訊號可能是這樣的:

它可能表示的資訊就是在八分音符的這半拍裡面, 它會有一個跟這個音符音高表示的音一樣的頻率的正弦波出現, 也就是上面那種正弦波

所以, 上圖的時域上的正弦波可以用下圖頻域上一個音高來表示.

相互表示

在演奏會上, 音樂家手裡拿的肯定是長得跟下面的"頻域"上的譜子, 而不是很多音符演奏出去之後的交錯的時域上的譜子(類似於下面這樣?)

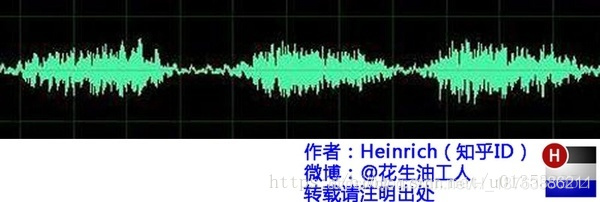
為啥? 是因為頻域在某些時候能更精確簡潔反應時域上的變化

那既然知道了從頻域到時域的意義, 可是我們一般能見到的也只有時域上的譜子啊, 我們怎麼搞成頻域上面的?

答案是通過傅立葉變換可以將時域上的東西轉化到頻域上去.

又或者我們知道了頻域上的資訊, 怎麼去還原這個時域上的資訊?

答案是通過傅立葉逆變換, 可以將頻域還原回時域上面去.

傅立葉變換

傅立葉變換和級數, 展開的關係

傅立葉級數假定了函數是連續的而且是周期函數, 傅立葉變換則將所有函數看成了一個週期無限大的函數, 去做這個傅立葉級數的展開.

個人感覺本質上傅立葉變換就是更強的傅立葉展開成為傅立葉級數.

從傅立葉展開說起

我們先不看傅立葉變換, 普通的傅立葉展開就可以將時域訊號轉化為頻域的訊號. 那咋做呢?

既然我們說任何函數都可以看成是多個三角函數的疊加, 那是不是我們也可以把一個函數分解成多個三角函數的和?

那必然可以, 我們這裡取一個只有奇數次的三角函數相加的例子:

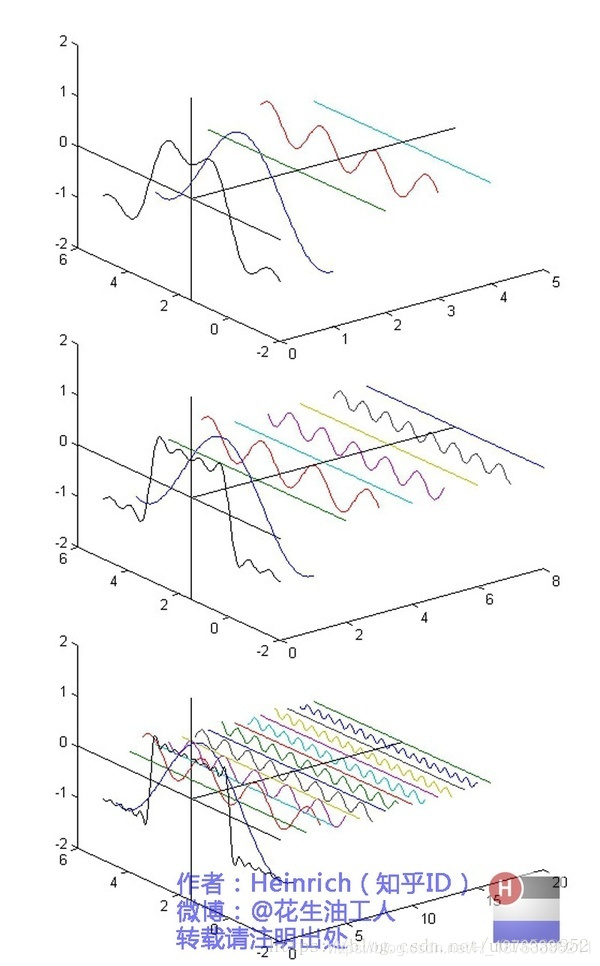
好, 你已經得到了離散的頻域的分量.

咋得到的呢? 這就要看傅立葉變換的輸入輸出是啥了.

傅立葉變換的輸入輸出

傅立葉變換的輸入是一個隨時間t變化的函數 $f(t)$
傅立葉變換的輸出是一個隨頻率w變化的函數 $F(w)$

其中這個w啊, 就是三角函數裡面那個頻率啊!

如果你把上面那個圖的第一條線的頻率看作是1, 那麼因為後面的頻率都是它的整數倍, 所以後面的頻率也是一系列的整數.

對於每個w, 你都能知道一個它的具體形式中 $A\sin (wx)$裡面的$A和w$, 那既然w是自變數, A理所應當的就成為了因變數. 也就是對應的 $F(w)=A$. (當然這只是一個形式化的理解)

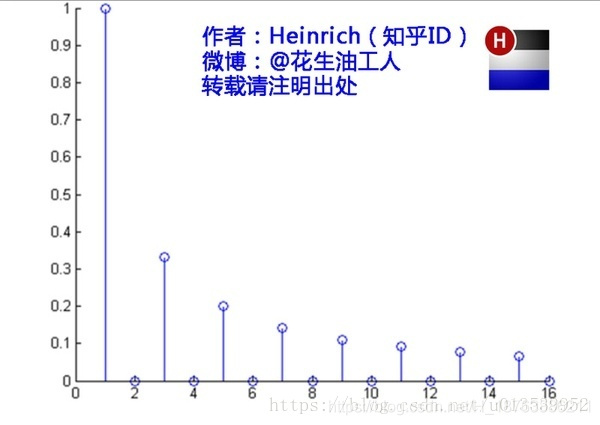
等下哈, 你把這三個圖放在一起看, 你看看能發現什麼 >_<

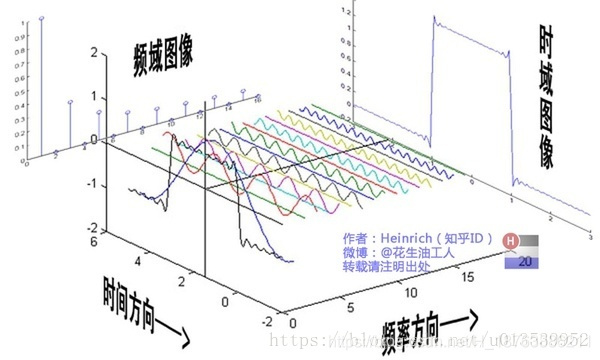
是不是非常妙?

復指數形式的傅立葉級數(推導)

啥? 為啥我一開始這麼明白的東西還能扯上覆指數?

別急, 且聽我慢慢道來.

你看那個優美的式子(w是那個最小的頻率, n就是對應頻譜的那個下標)

$$\begin{gathered} f(t)=\sum _{n=0}^{+\infty }{a}_n\cos (nwt)+b_n\sin (nwt) \\ {e}^{inwt}=\cos (nwt)+i\sin (nwt) \\ {e}^{-inwt}=\cos (nwt)-i\sin (nwt) \end{gathered}$$

是不是可以做做等價變換啊? 那就先看看三角函數怎麼變換吧

$$\begin{gathered} \cos (nwt)=\frac{e^{inwt}+e^{-inwt}}{2} \\ \sin (nwt)=\frac{e^{inwt}-e^{-inwt}}{2i} \end{gathered}$$

然後我們就把它帶到上面那個傅立葉展開式中去

$$\begin{gathered} f(t)=\sum _{n=0}^{+\infty }{a}_n\frac{e^{inwt}+e^{-inwt}}{2}+b_n\frac{e^{inwt}-e^{-inwt}}{2i} \\ =\sum _{n=0}^{+\infty }\frac{a_n\cdot e^{inwt}}{2}+\frac{a_n\cdot e^{-inwt}}{2}+\frac{-i{b}_n\cdot e^{inwt}}{2}+\frac{i{b}_n\cdot e^{-inwt}}{2} \\ =\sum _{n=0}^{+\infty }{e}^{inwt}\frac{a_n-i{b}_n}{2}+\sum _{n=0}^{+\infty }{e}^{-inwt}\frac{a_n+i{b}_n}{2} \end{gathered}$$

然後我們把後半部分式子的n反過來, 也就是

$$\sum _{n=0}^{+\infty }{e}^{-inwt}\frac{a_n+i{b}_n}{2}=\sum _{n=0}^{-\infty }{e}^{inwt}\frac{a_{-n}+i{b}_{-n}}{2}$$

然後把它帶回去原來的式子, 並且單獨把n=0給拿出來

$$f(t)=\sum _{n=1}^{+\infty }{e}^{inwt}\frac{a_n-i{b}_n}{2}+\sum _{n=-1}^{-\infty }{e}^{inwt}\frac{a_{-n}+i{b}_{-n}}{2}+\sum _{n=0}^0{e}^{inwt}{a}_0$$

然後你看它是不是都有$e^{inwt}$?那我們不如?

$$\begin{gathered} f(t)=\sum _{n=-\infty }^{+\infty }{c}_n{e}^{inwt} \\ {c}_n=\{\begin{array}{ll}{a}_0& ,n=0\\ \frac{a_n-i{b}_n}{2}& ,n>0\\ \frac{a_{-n}+i{b}_{-n}}{2}& ,n<0\end{array} \end{gathered}$$

展開說說?

$$\begin{gathered} \{\begin{array}{l}{a}_0=\frac{1}{T}{\int }_0^{T}f(t)dt\\ a_n=\frac{2}{T}{\int }_0^{T}f(t)\cos (nwt)dt\\ b_n=\frac{2}{T}{\int }_0^{T}f(t)\sin (nwt)dt\end{array} \\ \{\begin{array}{l}{a}_n=\{\begin{array}{ll}{c}_n& ,n=0\\ c_n+c_{-n}& ,n>0\end{array}\\ b_n=i(c_n-c_{-n}),n>0\end{array} \end{gathered}$$

然後我們把這個ab的求法帶到c裡面去, 看看c長啥樣?

先推導那個$c_n,n=0$

$$c_0=a_0=\frac{1}{T}{\int }_0^{T}f(t)dt=\frac{1}{T}{\int }_0^{T}f(t)e^{inwt}dt,n=0$$

然後推導$c_n,n>0$

$$\begin{array}{rl}{c}_n=\frac{a_n-i{b}_n}{2}& =\frac{1}{2}(\frac{2}{T}{\int }_0^{T}f(t)\cos (nwt)dt-i\frac{2}{T}{\int }_0^{T}f(t)\sin (nwt)dt)\\ & =\frac{1}{T}{\int }_0^{T}f(t)(\cos (nwt)-i\sin (nwt))dt\\ & =\frac{1}{T}{\int }_0^{T}f(t)e^{-inwt}dt\end{array}$$

然後推導$c_n,n<0$

$$\begin{array}{rl}{c}_n=\frac{a_{-n}+i{b}_{-n}}{2}& =\frac{1}{2}(\frac{2}{T}{\int }_0^{T}f(t)\cos (-nwt)dt+i\frac{2}{T}{\int }_0^{T}f(t)\sin (-nwt)dt)\\ & =\frac{1}{T}{\int }_0^{T}f(t)(\cos (-nwt)+i\sin (-nwt))dt\\ & =\frac{1}{T}{\int }_0^{T}f(t)e^{i(-nwt)}dt\\ & =\frac{1}{T}{\int }_0^{T}f(t)e^{-inwt}dt\end{array}$$

哎? 是不是長得非常一樣啊? 那確實啊! 整理一下

$$c_n=\frac{1}{T}{\int }_0^{T}f(t)e^{-inwt}dt,n\in Z$$

讓我們迴歸本源($w$是一個常數, 表示最小的頻率尺度):

$$\begin{array}{rl}f(t)& =\sum _{n=0}^{+\infty }{a}_n\cos (nwt)+b_n\sin (nwt)\\ & =\sum _{n=-\infty }^{+\infty }{c}_n{e}^{inwt}\\ & =\frac{1}{T}\sum _{n=-\infty }^{+\infty }({\int }_0^{T}f(t)e^{-inwt}dt)e^{inwt}\end{array}$$

哦對了, 這裡補充一下, 為啥會從普通的實數域的$a,b$擴充套件到複數域的這個$c$.
我個人理解是: 原先通過兩個變數$(a,b)$來確定這個函數, 現在可以認為是$(c_r,c_i)$實部和虛部來確定的

復指數形式的傅立葉變換(結論)

$$\begin{gathered} f(t)=\sum _{n=-\infty }^{+\infty }{c}_n{e}^{inwt} \\ {c}_n=\frac{1}{T}{\int }_0^{T}f(t)e^{-inwt}dt,n\in Z \end{gathered}$$

非周期函數傅立葉變換(推導)

你看上面那個東西是不是都有一個最小的頻率w, 所有的w取值只能是離散的吧! 那能不能搞成連續的w呢?

等等, 似乎不用太麻煩, 如果我$w\to 0$足夠小, 是不是說所有值都能通過$W=nw$的形式去表示出來?

那就開始推式子唄, 開始從普通的離散過渡到連續上面去

$$F(nw)=c_n=\frac{1}{T}{\int }_0^{T}f(t)e^{-inwt}dt$$

讓我們取$w\to 0$, 帶進去看看?

$$\begin{array}{rl}f(t)& =\underset{w\to 0}{\lim }\sum _{n=-\infty }^{+\infty }\frac{1}{T}({\int }_{\frac{-T}{2}}^{\frac{T}{2}}f(t)e^{-inwt}dt)e^{inwt}\\ & =\underset{w\to 0}{\lim }\sum _{n=-\infty }^{+\infty }\frac{w}{2\pi }({\int }_{\frac{-T}{2}}^{\frac{T}{2}}f(t)e^{-inwt}dt)e^{inwt}\\ & =\underset{T\to +\infty }{\lim }\sum _{n=-\infty }^{+\infty }\frac{w}{2\pi }({\int }_{-\infty }^{+\infty }f(t)e^{-inwt}dt)e^{inwt}\end{array}$$

我們把這個求和啊給它換成積分好吧

$$\begin{array}{rl}f(t)& =\underset{T\to +\infty }{\lim }\sum _{n=-\infty }^{+\infty }\frac{w}{2\pi }({\int }_{-\infty }^{+\infty }f(t)e^{-inwt}dt)e^{inwt}\\ & =\underset{T\to +\infty }{\lim }{\int }_{-\infty }^{+\infty }\frac{w}{2\pi }({\int }_{-\infty }^{+\infty }f(t)e^{-inwt}dt)e^{inwt}dn\end{array}$$

既然$nw$都連續了, 那要不直接用$W$來代替$nw$唄, 給這個積分換個積分變數!

$$\begin{array}{rl}f(t)& =\underset{T\to +\infty }{\lim }{\int }_{-\infty }^{+\infty }\frac{w}{2\pi }({\int }_{-\infty }^{+\infty }f(t)e^{-inwt}dt)e^{inwt}dn\\ & ={\int }_{-\infty }^{+\infty }\frac{1}{2\pi }({\int }_{-\infty }^{+\infty }f(t)e^{-iWt}dt)e^{iWt}dW\\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }({\int }_{-\infty }^{+\infty }f(t)e^{-iWt}dt)e^{iWt}dW\end{array}$$

想想咱們傅立葉變換的輸出是啥來著?

輸出是對於某個頻率的強度$F(W)$啊! 這個是不是就是中間括號裡面的東西啊!

這就是傅立葉變換正變換 / 傅立葉變換

$$F(W)={\int }_{-\infty }^{+\infty }f(t)e^{-iWt}dt$$

然後還原回去的過程就是傅立葉變換逆變換 / 逆傅立葉變換

$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(W)e^{iWt}dW$$

非周期函數傅立葉變換(結論)

$$\begin{array}{rl}& F(W)={\int }_{-\infty }^{+\infty }f(t)e^{-iWt}dt\\ & f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(W)e^{iWt}dW\end{array}$$

上面這個叫傅立葉變換正變換 / 傅立葉變換, 下面這個叫傅立葉變換逆變換 / 逆傅立葉變換.

衝激函數及其性質

首先, 衝激函數並不是單位衝激函數, 單位衝激函數$n=0$的時候為1, 但是衝激函數$n=0$的時候為無窮. 而且通過廣義函數相關理論得到衝激函數的一些性質, 而且對於單位衝激函數, 除了第一條不同, 後兩條性質相同

$$\begin{gathered} \delta (x)=\{\begin{array}{ll}+\infty & ,x=0\\ 0& ,x\ne 0\end{array} \\ {\int }_{-\infty }^{\infty }\delta (x)dx=1 \\ \delta (x)\ast h(x)=h(x) \\ {\int }_{-\infty }^{\infty }\delta (x)h(x)dx=h(0) \end{gathered}$$

這些性質從簡單大學數學上是不好解釋的.記住就好，可以去查閱廣義函數、奇異函數相關內容

推奈奎斯特抽樣定理式子

原始抽樣序列的表示

$x_a(t)$為抽樣訊號, $x^{\prime }(t)$為理想抽樣訊號, $p(t)={\delta }_T(t)={\sum }_{m=-\infty }^{+\infty }\delta (t-mT)$為週期性的單位抽樣函數. 注意, 以上函數都是在t上取值連續的函數

$$\begin{gathered} x^{\prime }(t)=x_a(t)\cdot p(t)=x_a(t)\cdot \sum _{m=-\infty }^{+\infty }\delta (t-mT) \\ =\sum _{m=-\infty }^{+\infty }{x}_a(t)\delta (t-mT) \end{gathered}$$

因為$\delta (t-mT)$當且僅當$t=mT$的時候有值, 因此可以認為上式為:

$$x^{\prime }(t)=\sum _{m=-\infty }^{+\infty }{x}_a(t)\delta (t-mT)=\sum _{m=-\infty }^{+\infty }{x}_a(mT)\delta (t-mT)$$

求抽樣完成後序列頻譜與原頻譜關係

$X_a(i\Omega )=F_{x_a}(\Omega )$, ${\Delta }_T(i\Omega )=F_{{\delta }_T}(\Omega )$, $X_a^{\prime }(i\Omega )=F_{x_a^{\prime }}(\Omega )$也就是對應的頻譜的輸出結果

$$\begin{gathered} x_a^{\prime }(t)={\delta }_T(t)\cdot x_a(t) \\ {X}_a^{\prime }(i\Omega )=\frac{1}{2\pi }[{\Delta }_T(i\Omega )\ast X_a(i\Omega )] \end{gathered}$$

(第二個式子還沒學會怎麼證明, 等學會了補上>_<)

那麼我們就從${\Delta }_T(t)$開始求解吧

求解週期衝激函數傅立葉展開

首先明確一個事情, 就是我們這個衝激函數求出來之後會近似於原始的衝激函數.(不信你做做逆變換). 為啥要求這個傅立葉展開, 這是為了解決這個函數不好計算的問題

這個週期衝激函數是個周期函數, 所以直接用周期函數的傅立葉展開就行了${\Omega }_s$為抽樣頻率

$${\delta }_T(t)=\sum _{k=-\infty }^{+\infty }{c}_k{e}^{ik{\Omega }_{s}t}dt$$

然後周期函數的$c_k$求法帶進去

$$\begin{array}{rl}{c}_k& =\frac{1}{T}{\int }_{\frac{-T}{2}}^{\frac{T}{2}}{\delta }_T(t)e^{-ik{\Omega }_{s}t}dt\\ (展開{\delta }_T)& =\frac{1}{T}{\int }_{\frac{-T}{2}}^{\frac{T}{2}}\sum _{p=-\infty }^{+\infty }\delta (t-pT)e^{-ik{\Omega }_{s}t}dt\end{array}$$

發現只有$p=0$的時候, $t=0$在最靠近0的這個週期裡面. 所以上面這個式子可以寫成(利用一下衝激函數的性質)

$$\begin{array}{rl}{c}_k& =\frac{1}{T}{\int }_{\frac{-T}{2}}^{\frac{T}{2}}\sum _{p=-\infty }^{+\infty }\delta (t-pT)e^{-ik{\Omega }_{s}t}dt\\ & =\frac{1}{T}{e}^{-ik{\Omega }_{s}0}=\frac{1}{T}\end{array}$$

所以啊, 原來那個週期性衝激函數就可以被展開成

$${\delta }_T(t)=\frac{1}{T}\sum _{k=-\infty }^{+\infty }{e}^{ik{\Omega }_{s}t}$$

然後這個展開式的圖呢, 在最靠近0的這個區間裡啊, 大概長這樣(我只模擬了80層疊加, 而且是展開之後的疊加)

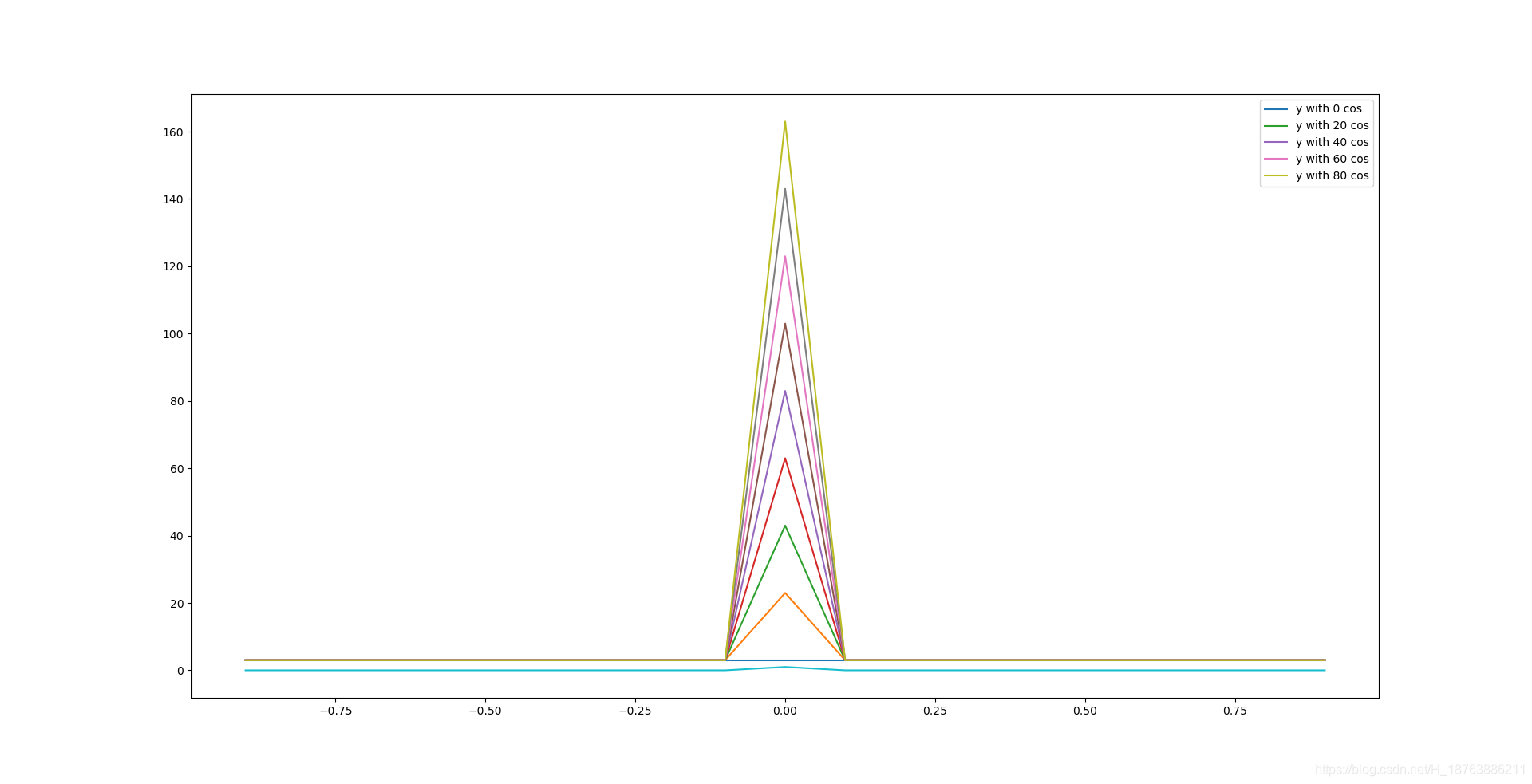
你看它這個趨勢就是在向無窮去疊加, 也就是去模擬這個週期衝激函數.

然後我們去考慮一下把這個東西給做一下傅立葉變換.

求解週期衝激函數的頻域

嗯, 列式子吧(看起來很簡單!), $FT[\cdot ]$ 表示傅立葉變換

$$\begin{array}{rl}{\Delta }_T(i\Omega )& =FT[\frac{1}{T}\sum _{k=-\infty }^{+\infty }{e}^{ik{\Omega }_{s}t}]\\ & =\frac{1}{T}\sum _{k=-\infty }^{+\infty }FT[e^{ik{\Omega }_{s}t}]\end{array}$$

然後我們看這個$FT[e^{ik{\Omega }_{s}t}]$, 它是不是很簡單做出來

它有一條性質, 也就是結果, 是$FT[e^{ik{\Omega }_{s}t}]=2\pi \delta (\Omega -k{\Omega }_s)$

然後帶進去就能得到:

$$\begin{array}{rl}{\Delta }_T(i\Omega )& =\frac{1}{T}\sum _{k=-\infty }^{+\infty }FT[e^{ik{\Omega }_{s}t}]\\ & =\frac{2\pi }{T}\sum _{k=-\infty }^{+\infty }\delta (\Omega -k{\Omega }_s)\\ & ={\Omega }_s\sum _{k=-\infty }^{+\infty }\delta (\Omega -k{\Omega }_s)\end{array}$$

什麼? 你非要推出上面那個性質來? 那就單獨開一節吧!

求解一個特殊的傅立葉變換(建議跳過)

求解下面這個式子

$$F(W)={\int }_{-\infty }^{+\infty }{e}^{ik{\Omega }_{s}t}\cdot e^{-iWt}dt$$

然後求解一下這個問題哈:

$$F(W)=\{\begin{array}{ll}0& ,W\ne k{\Omega }_s\\ +\infty & ,W=k{\Omega }_s\end{array}$$

哎你看, 這東西是不是衝激函數啊?那我們給它搞成衝激函數一樣的東西唄

$$F(W)=\delta (W-k{\Omega }_s)$$

但是這…真的對嗎?

讓我們利用一下逆傅立葉變換, 看看能得到些啥?

$$\begin{array}{rl}f(t)& =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(W)e^{iWt}dW\\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\delta (W-k{\Omega }_s)e^{iWt}dW\\ & =\frac{1}{2\pi }{e}^{ik{\Omega }_{s}t}\end{array}$$

哎?是不是少了個係數? 少了個係數$2\pi$哎, 那就搞進去唄

$$F(W)=2\pi \delta (W-k{\Omega }_s)$$

然後就得到了那個顯然成立的式子.

理想抽樣訊號頻譜

$$\begin{array}{rl}{X}_a^{\prime }(i\Omega )& =\frac{1}{2\pi }[(\frac{2\pi }{T}\sum _{k=-\infty }^{+\infty }\delta (\Omega -k{\Omega }_s))\ast X_a(i\Omega )]\\ & =\frac{1}{T}[\sum _{k=-\infty }^{+\infty }\delta (\Omega -k{\Omega }_s))\ast X_a(i\Omega )]\\ & =\frac{1}{T}\sum _{k=-\infty }^{+\infty }[\delta (\Omega -k{\Omega }_s)\ast X_a(i\Omega )]\\ & =\frac{1}{T}\sum _{k=-\infty }^{+\infty }[{\int }_{-\infty }^{+\infty }{X}_a(i\theta )\cdot \delta (\Omega -\theta -k{\Omega }_s)d\theta ]\\ & =\frac{1}{T}\sum _{k=-\infty }^{+\infty }{X}_a(i(\Omega -k{\Omega }_s))\\ & =\frac{1}{T}\sum _{k=-\infty }^{+\infty }{X}_a(i(\Omega -k\frac{2\pi }{T}))\end{array}$$

這不就是把原先的那個$X_a$給它左右平移$\frac{2\pi }{T}$嘛, 那就是說的延拓週期

$${\Omega }_s=\frac{2\pi }{T}=2\pi f_s$$

就是抽樣頻率啊!

$$\begin{array}{rl}{X}_a^{\prime }(i\Omega )& =\frac{1}{T}\sum _{k=-\infty }^{+\infty }{X}_a(i(\Omega -k\frac{2\pi }{T}))\\ & =\frac{{\Omega }_s}{2\pi }\sum _{k=-\infty }^{+\infty }{X}_a(i(\Omega -k{\Omega }_s))\end{array}$$