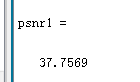立體影象編碼解碼

     根據相關參考資料說明，影象編碼解碼的大致結構框圖如下所示：

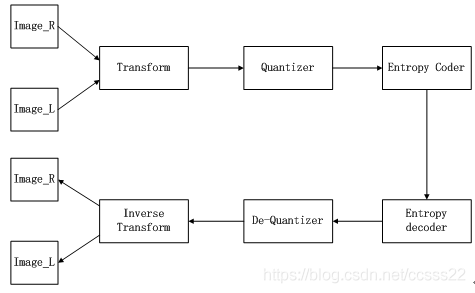
    本系統，我們主要將完成這個結構框圖中介紹的各個模組。

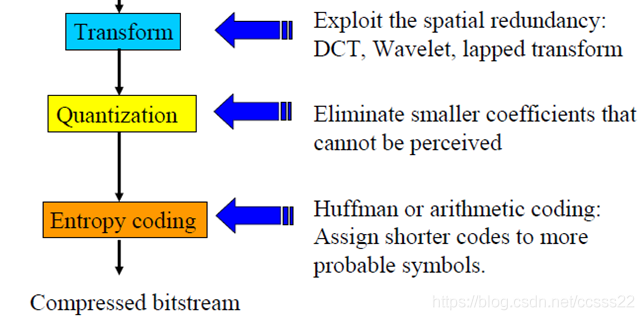
2.各個模組設計與模擬

function im_encode(left_name, right_name, parameter);

傳送端的說明

2.1 獲得左右兩個影象

·MATLAB程式碼

imag_L = imread('stereo_images/corridor1.pgm');

imag_R = imread('stereo_images/corridor2.pgm');

figure(1);

subplot(121),imshow(imag_L);title('left');

subplot(122),imshow(imag_R);title('right');

·模擬效果

圖2 左右眼睛看到的影象

·程式碼說明

    通過讀取兩個圖片，來模擬人兩個眼睛所看到的影象。

2.2 Transform模組

    這個模組主要使用DCT變換，但是這裡設計到一個問題，就是將兩個圖片訊號變為一路訊號的問題。就本課題而言，這裡有以下幾個方法實現；

·由於這兩個圖片是雙目訊號，所以可以先進行立體匹配得到一個圖片，然後再接收端分解成兩個雙目圖片；

·由小波分解進行融合得到一路訊號，然後在接收端進行反變換，但是這種做法也較複雜。

·進行圖片的取樣處理，對兩個圖片進行間隔取樣，然後在接收端進行內插得到原影象，這種方法比較簡單，本模組採用這個方法。

    其程式碼如下所示：

 

[R,L] = size(imag_L);

for i = 1:R

    for j = 1:L

         if mod(i+j,2)==0

         image(i,j) =  imag_L(i,j);

         else

         image(i,j) =  imag_R(i,j);   

         end

    end

end

 

2.3 DCT變換

   我們在這裡使用MATLAB內部的dct2函數。這裡就不多做介紹了。其模擬結果如下所示：

其程式碼如下所示：

DCT_out = dct2(image);

 

2.4 ZIGZAG演演算法

    其基本原理如下所示：

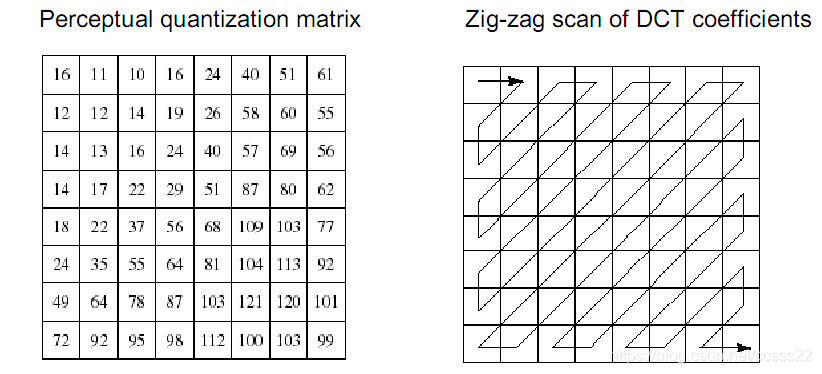
通過這個方法，我們可以將一個影象的二維資料變為一個序列的資料流。

其對應的程式碼如下所示：

function [y]=toZigzag(x)

% transform a matrix to the zigzag format

 [row col]=size(x);

 

if row~=col

   disp('toZigzag() fails!! Must be a square matrix!!');

   return

end

y=zeros(row*col,1);

count=1;

for s=1:row

   if mod(s,2)==0

      for m=s:-1:1

         y(count)=x(m,s+1-m);

         count=count+1;

      end;

   else

      for m=1:s

         y(count)=x(m,s+1-m);

         count=count+1;

      end

   end

end

if mod(row,2)==0

   flip=1;

else

   flip=0;

end

for s=row+1:2*row-1

   if mod(flip,2)==0

      for m=row:-1:s+1-row

         y(count)=x(m,s+1-m);

         count=count+1;

      end

   else

      for m=row:-1:s+1-row

         y(count)=x(s+1-m,m);

         count=count+1;

      end;

   end;

   flip=flip+1;

end

 

　　μ律（m-Law）壓擴主要用在北美和日本等地區的數位電話通訊中。m為確定壓縮量的引數，它反映最大量化間隔和最小量化間隔之比，通常取100≤m≤500。由於m律壓擴的輸入和輸出關係是對數關係，所以這種編碼又稱為對數PCM。

　　A律（A-Law）壓擴主要用在歐洲和中國大陸等地區的數位電話通訊中。A為確定壓縮量的引數，它反映最大量化間隔和最小量化間隔之比。A律壓擴的前一部分是線性的，其餘部分與μ律壓擴相同。

15折線特性給出的小訊號的號誌噪比約是13折線特性的兩倍。      但是，對於大訊號而言，15折線特性給出的號誌噪比要比13折線特性時稍差。在保證小訊號的量化間隔相等的條件下，均勻量化需要11位元編碼，而非均勻量化只要7位元就夠了。

    其對應的待明如下所示：

function ypcm=mulaw(yn)

x=yn;

s=sign(x);                            

x=abs(x);                            

ypcm=zeros(length(x),1);

%進行基於15折線的分段對映

for i=1:length(x)                  

    if x(i)<1/255              %序列值位於第1折線

        ypcm(i)=255/8*x(i);

    elseif x(i)<3/255           %序列值位於第2折線

        ypcm(i)=255/16*x(i)+1/16;

    elseif x(i)<7/255           %序列值位於第3折線

        ypcm(i)=255/32*x(i)+5/32;

    elseif x(i)<15/255          %序列值位於第4折線

        ypcm(i)=255/64*x(i)+17/64;

    elseif x(i)<31/255          %序列值位於第5折線

        ypcm(i)=255/128*x(i)+49/128;

    elseif x(i)<63/255          %序列值位於第6折線

        ypcm(i)=255/256*x(i)+129/256;

    elseif x(i)<127/255         %序列值位於第7折線

        ypcm(i)=255/512*x(i)+321/512;

    else                     %序列值位於第8折線

        ypcm(i)=255/1024*x(i)+769/1024;

    end

end

ypcm=ypcm.*(2^7);   

ypcm=floor(ypcm);

ypcm=ypcm.*s;

2.6 編碼模組

    傳送的最後我們需要將量化後的資料進行壓縮，得到二進位制位元率進行傳送，這裡我們使用huffman編碼。Huffman編碼的基本原理如下所示：

哈夫曼編碼是用於資料檔案壓縮的一個十分有效的編碼方法，其壓縮率通常在20％～90％之間。哈夫曼編碼演演算法使用字元在檔案中出現的頻率表來建立一個0,1串，以表示各個字元的最優表示方式。

      它是一種編碼方式，哈夫曼編碼是可變字長編碼(VLC)的一種。 Huffman於1952年提出一種編碼方法，該方法完全依據字元出現概率來構造異字頭的平均長 度最短的碼字，有時稱之為最佳編碼，一般就叫作Huffman編碼。 以哈夫曼樹─即最優二元樹，帶權路徑長度最小的二元樹，經常應用於資料壓縮。 在計算機資訊處理中，「哈夫曼編碼」是一種一致性編碼法（又稱"熵編碼法"），用於資料的無失真耗壓縮。這一術語是指使用一張特殊的編碼表將源字元（例如某檔案中的一個符號）進行編碼。這張編碼表的特殊之處在於，它是根據每一個源字元出現的估算概率而建立起來的（出現概率高的字元使用較短的編碼，反之出現概率低的則使用較長的編碼，這便使編碼之後的字串的平均期望長度降低，從而達到無失真壓縮資料的目的）。這種方法是由David.A.Huffman發展起來的。 例如，在英文中，e的出現概率很高，而z的出現概率則最低。當利用哈夫曼編碼對一篇英文進行壓縮時，e極有可能用一個位(bit)來表示，而z則可能花去25個位（不是26）。用普通的表示方法時，每個英文字母均佔用一個位元組（byte），即8個位。二者相比，e使用了一般編碼的1/8的長度，z則使用了3倍多。倘若我們能實現對於英文中各個字母出現概率的較準確的估算，就可以大幅度提高無失真壓縮的比例。

根據變長最佳編碼定理，Huffman編碼步驟如下：

（1）將信源符號xi按其出現的概率，由大到小順序排列。

（2）將兩個最小的概率的信源符號進行組合相加，並重復這一步驟，始終將較大的概率分支放在上部，直到只剩下一個信源符號且概率達到1.0為止；

（3）對每對組合的上邊一個指定為1，下邊一個指定為0（或相反：對上邊一個指定為0，下邊一個指定為1）；

（4）畫出由每個信源符號到概率1.0處的路徑，記下沿路徑的1和0；

（5）對於每個信源符號都寫出1、0序列，則從右到左就得到非等長的Huffman碼。

其對應的程式碼如下所示：

function [compression,dict] = huffman_module(image);

s = image;

%entropy

p = hist(s,length(s)); 

idx=find(p~=0); 

prob=p(idx)/length(s);

entropy=-prob*log2(prob)';

%redundancy

entropymax=log2(length(prob));

redundancy=(entropymax-entropy)/entropymax;

reff=sort(s);

ref2=reff(2:end);

ref=reff(1:end-1);

chg=ref2-ref;

idx2=find(chg~=0);

sig=ref2(idx2);

symbols=[ref(1);sig];

%huffman table

set(0,'RecursionLimit',2000);

[dict,avglen] = huffmandict(symbols,prob);

% %huffman encoder

compression = huffmanenco(s,dict);

3.各個模組設計與模擬

3.系統總體模擬說明

    系統的模擬結果如下所示：

 

讀入兩個圖片

 

 

 

 

 

DCT變換值

 

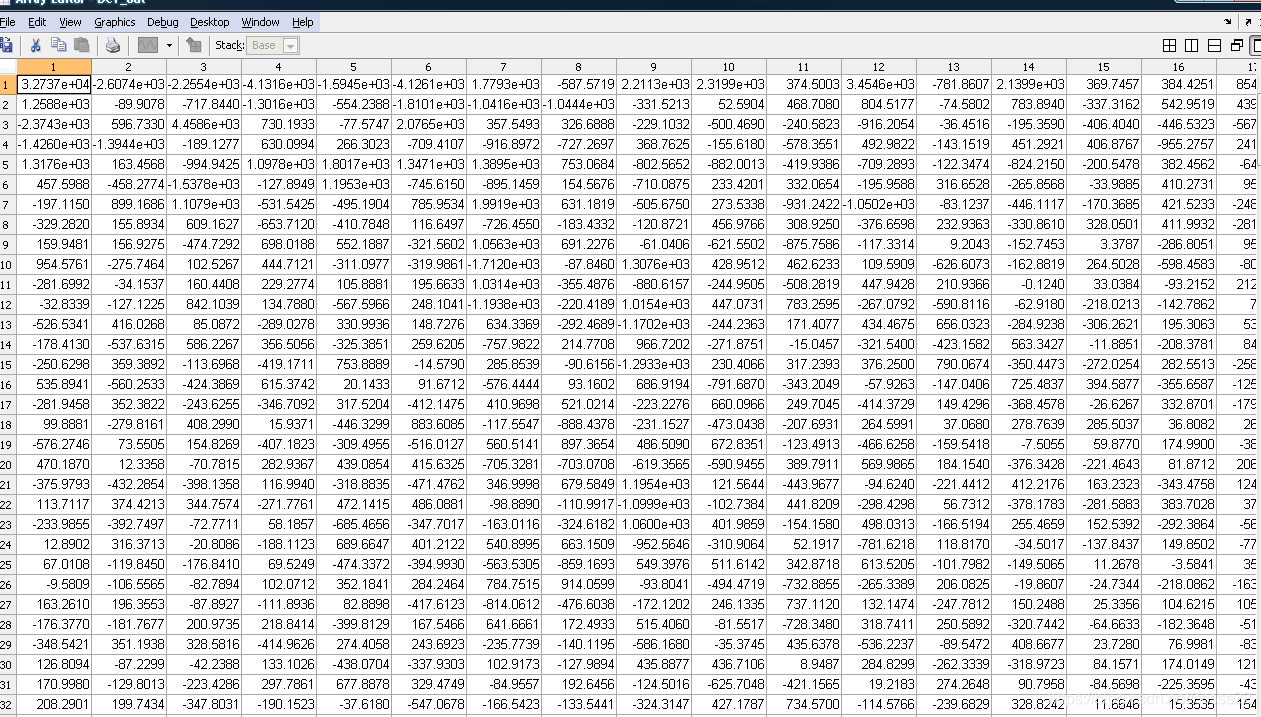
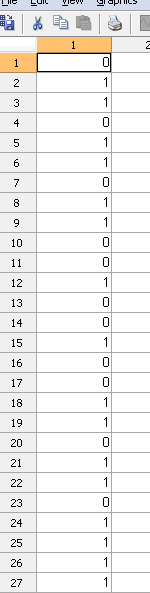
量化值

 

壓縮位元流

 

 

最後接收到的雙目圖片。

最後我們可以得到PSNR值為