【upc】2020年秋季組隊訓練賽第十三場B Bouldering | 維度最短路

問題 B: Bouldering

時間限制: 1 Sec  記憶體限制: 128 MB  Special Judge
提交 狀態

題目描述

After a few particularly long afternoons of procrastinating in his box, playing video games all night long, Carl decided it was finally time to start his New Year’s Resolution – going to the bouldering gym.
There, he took to one of the easier walls and tried to make his way up. Unfortunately, he could never quite reach the top, as he would always run out of stamina and fall down.
While climbing, he noticed the holds all have different shapes with some of them being much harder to hold than others, so gripping them uses up different amounts of stamina. Frustrated, he asks one of the regulars at the bouldering hall how to scale the wall – you. Show him the shortest way up that he can take without running out of stamina.
The bouldering wall is a rectangular grid of cells of size 1 × 1 where holds can be installed. For this problem we do not consider the varying sizes of the holds, so you can assume them to be the shape of a singular point exactly in the middle of the cell. Carl can only move from one hold to another if their distance (the Euclidean distance between the centres of the cells) does not exceed his arms’ reach.

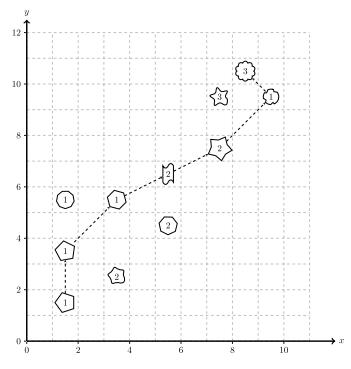
Figure B.1: Sample test case 1

輸入

The input consists of:
• A line with four integers h, w, r and s (2 ≤ h ≤ 25, 1 ≤ w ≤ 25, 1 ≤ r ≤ 3, 1 ≤ s ≤ 109 ) where h and w are the height and width of the bouldering wall, r is the reach of Carl’s arms and s is a numerical representation of Carl’s stamina.
• h lines, each with w characters, describing the holds on the bouldering wall. Each character is either a digit c (1 ≤ c ≤ 9), which means that a hold with difficulty c is installed at this position, or 「.」, which means there is no hold installed.
The first line corresponds to the top of the bouldering wall and the last line to the bottom. 
A sequence of holds is a valid route for Carl if the following conditions are satisfied:
• The route starts at the bottommost hold and ends at the topmost hold. There will always be a unique bottommost and a unique topmost hold, and these are guaranteed to be distinct.
• The sum of difficulty levels of the used holds is at most s.
• The Euclidean distance between any two consecutive holds along the route is at most r.

輸出

Output the total length of a shortest route Carl can climb to reach the topmost hold without running out of stamina. Your answer should have an absolute or relative error of at most 10−6.
If it is not possible for Carl to reach the top, output impossible.

樣例輸入 Copy

12 11 3 11
...........
........3..
.......3.1.
...........
.......2...
.....2.....
.1.1.......
.....2.....
.1.........
...2.......
.1.........
...........

樣例輸出 Copy

13.543203766865055

題目大意：

從最下面是數位的點出發，每次能前往半徑在<=r以內的點，到達的點的費用是該點的數位

求最下面到最上面的在費用不超過S的情況下的最短路

題目大意：

25*25*25*25直接暴力建圖

建圖之後，跑維度最短路

將第二維S,spfa

這題卡了鏈式前向星..

Code:

/*** keep hungry and calm CoolGuang!***/
#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define debug(x) cout<<#x<<":"<<x<<endl;
#define _CRT_SECURE_NO_WARNINGS
using namespace std;
typedef  long long ll;
typedef unsigned long long ull;
const ll INF= 1e18;
const int maxn =1e5+7;
const int mod= 20007;
inline bool read(ll &num)
{char in;bool IsN=false;
    in=getchar();if(in==EOF) return false;while(in!='-'&&(in<'0'||in>'9')) in=getchar();if(in=='-'){ IsN=true;num=0;}else num=in-'0';while(in=getchar(),in>='0'&&in<='9'){num*=10,num+=in-'0';}if(IsN) num=-num;return true;}
ll n,m,p;
double d[26][26][6252];
bool vis[26][26][6252];
char mp[50][50];
ll sx,sy,ex,ey;
vector< pair<int,int> >v[50][50];
double dis(double ax,double ay,double bx,double by){
    return sqrt((ax-bx)*(ax-bx) + (ay-by)*(ay-by));
}
struct node{
    ll w,idx,idy;
};
struct Node{
    int x,y,next;
}edge[maxn*2];
int head[26][26];
ll cnt = 0;
void addedge(int ux,int uy,int vx,int vy){
    edge[cnt] = Node{vx,vy,head[ux][uy]};
    head[ux][uy] = cnt++;
}
void spfa(){
    queue<node>q;
    q.push(node{mp[sx][sy]-'0',sx,sy});
    for(int i=1;i<=n;i++)
        for(int k=1;k<=m;k++)
            for(int j=0;j<=p;j++)
                d[i][k][j] = INF;
    d[sx][sy][mp[sx][sy]-'0'] = 0;vis[sx][sy][mp[sx][sy]-'0'] = 1;
    double minl = INF;
    while(!q.empty()){
        node u = q.front();q.pop();
        int x = u.idx,y = u.idy,w = u.w;
        vis[x][y][w] = 0;
        if(x==ex&&y==ey){
            minl = min(minl,d[x][y][w]);
            continue;
        }
        for(int i=head[x][y];~i;i=edge[i].next){
            int dx = edge[i].x,dy = edge[i].y,dw = u.w + mp[dx][dy]-'0';
            if(dw<=p && d[dx][dy][dw] > d[x][y][w] + dis(dx*1.0,dy*1.0,x*1.0,y*1.0)){
                d[dx][dy][dw] = d[x][y][w] + dis(dx,dy,x,y);
                if(!vis[dx][dy][dw]){
                    q.push(node{dw,dx,dy});
                    vis[dx][dy][dw] = 1;
                }
            }
        }
    }
    if(minl == INF)
        printf("impossible\n");
    else printf("%.16lf\n",minl);
    return ;
}
int main(){
    ll t;
    memset(head,-1,sizeof(head));
    read(n);read(m);read(t);read(p);
    for(int i=1;i<=n;i++)
        scanf("%s",mp[i]+1);
    ll as = 0;
    int f = 0;
    for(int i=1;i<=n;i++){
        for(int k=1;k<=m;k++){
            if(mp[i][k] != '.'){
                if(!f) sx = i,sy = k;
                ex = i,ey = k;
                f = 1;
                as += mp[i][k] - '0';
            }
        }
    }
    p = min(p,as);
    for(int i=1;i<=n;i++){
        for(int k=1;k<=m;k++){
            for(int j=1;j<=n;j++){
                for(int l=1;l<=m;l++){
                    if(i==j && k==l) continue;
                    if(mp[i][k] != '.' && mp[j][l] != '.'){
                        if((i-j)*(i-j) + (l-k)*(l-k) <= t*t) addedge(i,k,j,l);
                    }
                }
            }
        }
    }
    spfa();
    return 0;
}