[演算法系列]遞迴應用——二元樹(2):一種帶資訊遞迴返回的求解方式
[演算法系列]遞迴應用——二元樹(2):一種帶資訊遞迴返回的求解方式
本文是遞迴系列文的第七篇,和上篇文章類似,介紹BinaryTree的解題思路。這裡介紹一種和「遍歷」行為類似的,自下而上遞迴返回資訊的解題思路。其規則的寫法、並不複雜的思路,可解決大多bintree中與子樹有關的問題(但願吧哈哈哈)
0.引子:求二元樹節點中的最大值和最小值
此題當然可以通過遍歷整棵二元樹,將遍歷途中遇到的最大值和最小值進行儲存。遍歷完成後maxVal和minVla即為所求:
class MaxAndMinInBinTree{
int maxVal = Integer.MIN_VALUE;
int minVal = Integer.MAX_VALUE;
public int[] getMinMaxInBT(TreeNode node){
process(node);
return new int[]{maxVal, minVal};
}
public void process(TreeNode node){
if(node == null) return;
maxVal = Math.max(node.val , maxVal);
minVal = Math.min(node.val, minVal);
process(node.left);
process(node.right);
}
}
那麼這道題目除了用 二元樹的 」遍歷「 思路,還可以怎麼想呢?
回憶我們求二元樹的高度時用到的思路:
當前子樹的高度 =max( 左子樹的高度 ,右子樹高度)+ 1- 在遞迴中逐漸返回到頭結點:
樹的高度 = max(根的子樹高度,根的右子樹高度) +1
這其實就是一種和遍歷思路稍顯區別的,俺將其命名為帶資訊返回的求解思路。那麼如果將其運用到求整棵樹的最大最小值時,就可以自然而然地有如下想法:
當前子樹的最大值 = max(左子樹最大值,右子樹最大值,當前節點的值)當前子樹的最小值 = min(左子樹最小值,右子樹最小值,當前節點的值)- 在遞迴中逐漸向上返回到根節點。
該思路其一般可寫成如下框架:
public ReturnData process(TreeNode node){
if(node == null){
//處理節點為空的情況,也是」遞「到達的最深處,」歸「上去的起點
}
ReturnData leftDate = process(node.left);
ReturnData rightData = process(node.right);
return new ReturnData(
//根據當前節點考慮可能性,構造當前要向上返回的資訊集
)
}
下面來解釋一波上述的虛擬碼:
-
ReturnData是自定義的一個類,裡面包含的是遞迴過程中每次需要返回的所有資訊
-
看整個process函數框架,看過我前面詳解遞迴的小夥伴應該比較清楚:node == null 實際上就是邊界條件,是遞迴的出口,在此處我們需要拿捏最小問題的處理方式。
緊接著,是兩個遞迴呼叫process的過程,用leftData和rightData去接收左子樹和右子樹的結果。這一點前面也提到過:該模式下process函數會一口氣走到最左下的為null的節點,然後再返回到右下,從葉節點開始,逐漸往上地返回。
在返回過程中,構建了一個新的ReturnData範例物件。這也就把所需要返回的資訊向上地」歸「到了根節點。
-
在新構建返回資訊的範例物件中,就是我們根據可能性進行構造的過程。
好了,現在看看用這個方法時怎樣操作的:
class MaxAndMinInBinTree2{
/* 這個題的返回資訊就是所要求的最大值,最小值 */
public static class ReturnData{
public int maxVal;
public int minVal;
public ReturnData(int maxVal , int minVal){
this.maxVal = maxVal;
this.minVal = minVal;
}
}
public void getMinMax(TreeNode node){
ReturnData data = process(node);
System.out.println(data.maxVal + " " + data.minVal);
}
private ReturnData process(TreeNode head){
/* 遞迴邊界條件,構造最初的返回資訊 */ */
if(head == null){
return new ReturnData(Integer.MIN_VALUE, Integer.MAX_VALUE);
}
ReturnData leftData = process(head.left);
ReturnData rightData = process(head.right);
/* 逐漸向上遞迴的資訊,由每一層的各種可能性決定:
比如:當前子樹的最大值 = max(左子樹最大值,右子樹最大值,當前節點的值) */
return new ReturnData(
Math.max(Math.max(leftData.maxVal ,rightData.maxVal),head.val),
Math.min(Math.min(leftData.minVal , rightData.minVal),head.val)
);
}
}
1.判斷一個二元樹是否平衡
在引子中,我們分別用」遍歷「和"遞迴資訊返回"兩種思路求得了一顆二元樹中最大最小值,可以體會一下這兩種思路的區別和聯絡。
看上去第二種方法要比第一種更繁瑣,其實不然。因為,求二元樹中最大值這種問題,天然就屬於是遍歷可解的問題,當然遍歷就好啦。
但是,」遍歷「固然好,有些問題並不適合用遍歷的方式做,比如一些直接或間接與子樹有關的問題,比如就求一棵樹中滿足xxx條件的最大子樹,或者像這個」 判斷一個二元樹是否平衡「。下面來體會一下。
(1)設計ReturnData。
判斷是否平衡,需要一個isBalance的boolean變數來判斷。另外,判斷是否平衡實際上是根據左右子樹的高度差來決定的,因此還需要一個int h來儲存當前節點高度。在遞迴過程中傳遞這兩個值
(2)思考遞迴邊界條件。
依舊是head為null的情況,此時返回的資訊為isBalance=true,h=0,
(3)考慮每一次遞迴返回資訊中的個屬性賦值的可能性。
當前樹為平衡樹的條件為:左子樹為平衡的 && 右子樹為平衡的 && 左右子樹高度差<=1
因此,若左子樹不平衡,直接返回不平衡。右子樹不平衡,直接返回不平衡。高度差 > 1直接返回不平衡。
三者都通過了,就可在返回的資訊中把isBalance置為true,同時求其高度了。
class CheckBlance{
public static class ReturnData{
public boolean isBalance;
public int h;
public ReturnData(boolean isB, int h){
this.isBalance = isB;
this.h = h;
}
}
public ReturnData process(TreeNode head){
if(head == null){
return new ReturnData(true ,0);
}
ReturnData leftReturnData = process(head.left);
/*當左子樹不平衡時,當前樹定不平衡,可以不用再考慮右樹了。
這裡isB為false,直接返回到根處都不為平衡,
因此h實際上沒啥用
*/
if(!leftReturnData.isBalance)
return new ReturnData(false, 0);
ReturnData rightRetunrData =process(head.left);
//當左子樹不平衡時,當前樹定不平衡,可以不用再考慮當前節點了
if(!rightRetunrData.isBalance)
return new ReturnData(false,0);
//判斷平衡調節並返回
if(Math.abs(leftReturnData.h - rightRetunrData.h) > 1 )
return new ReturnData(false,0);
//能到這個位置,說明一定是平衡的,此時h才有他的用武之地
return new ReturnData(true , Math.max(leftReturnData.h , rightRetunrData.h) + 1);
}
}
2.求二元樹中最大的二叉搜尋子樹
通過上面的兩道可以看出這種方法還是挺可以的叭~
給一顆二元樹,返回該二元樹中最大的二叉搜尋子樹,比如下圖中的最大二叉搜尋子樹為紅圈中部分。
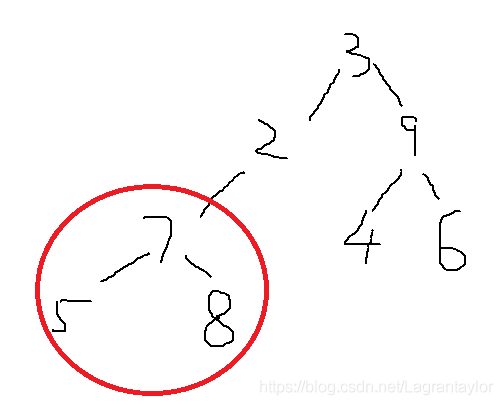
(1)設計ReturnData。
ReturnData需要四個資訊:
-
當前節點的最大子BST的size:
size。這個不用解釋了吧,最後要求的就是這個
-
當前節點的最大子BST的頭結點:
head。考慮一下,若左子樹的head是當前的左子樹,右子樹的head就是當前節點右子樹,是不是可能這三個連成一塊變成一個更大的BST呢?
-
當前節點的最小值和最大值
光是滿足2是不夠的,還得需要左子樹的最大值小於當前節點值,右子樹的最小值大於當前節點值才行。
(2)思考遞迴邊界條件。
當節點為null時。size為0,maxHead為null,最大值儲存系統最小值,最小值儲存系統最大值
(3)考慮每一次遞迴返回資訊中的個屬性賦值的可能性。
-
size:有三種可能:
左子樹的子BST的size最大時,
size = leftData.size右子樹的子BST的size最大時,
size = rightData.size左子樹、右子樹、當前節點連成一個BST時,size為
leftData.size + 1+ rightData.size -
head:同樣是三可能:
head = leftData.head
head = rightData.head
head = 當前節點
-
min 和 max,
考察左子樹的min、max,右子樹min、max和當前節點值即可
下面為程式碼
class FindSubBST{
public static class ReturnData{
public int size;
public TreeNode head;
public int min;
public int max;
public ReturnData(int size,TreeNode head,int min ,int max){
this.size = size;
this.head = head;
this.min = min;
this.max = max;
}
}
public Node getMaxSizeSubBST(TreeNode head){
return process(head).head;
}
public ReturnData process(TreeNode head){
if(head == null){
return new ReturnData(0,null,Integer.MAX_VALUE,Integer.MIN_VALUE);
}
TreeNode left = head.left;
TreeNode right = head.right;
ReturnData leftData = process(left);
ReturnData rightData = process(right);
/* 左孩子就是左BST的頭 右孩子也是右子BST的頭
且
左孩子的最大值小於當前節點值
右孩子的最小值小於當前節點值
此時將三個部分合並,即為所求
*/
int includeItSelf = 0;
if(leftData.head == left && rightData.head == right
&& leftData.max < head.val && rightData.min > head.val)
includeItSelf = leftData.size + 1 + rightData.size;
/*
maxSize的三種可能性:
左子樹,右子樹,才求的三合一
*/
int p1 = leftData.size;
int p2 = rightData.size;
int maxSize = Math.max(Math.max(p1,p2),includeItSelf);
/*
maxHead的三種可能性:
maxSize為左子樹時: maxHead為左子樹頭
maxSize為右子樹時: maxHead為右子樹頭
maxSize為includeItSelf時 : 說明已經三者合1,maxHead為當前節點
*/
TreeNode maxHead = p1 > p2 ? leftData.head : rightData.head;
if(maxSize == includeItSelf)
maxHead = head;
/* 所有資訊的所有可能性討論完畢,構建一個新物件返回 */
return new ReturnData(maxSize, maxHead ,
Math.min(Math.min(leftData.min, rightData.min),head.val),
Math.min(Math.max(leftData.max, rightData.max),head.val)
);
}
}
3.求一顆二元樹上的最遠距離
二元樹中,一個節點可以往上走和往下走,那麼從節點A總能走到節點B。節點A走到節點B的距離為:A走到B最短路徑上的節點個數。
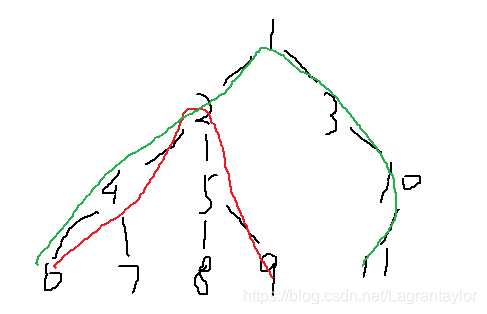
如上圖所示的二元樹中,最遠距離為從6或7或8或9出發,連到11的距離(綠色線為其中一個路線)
在其左子樹中,紅色線代表的路徑。
【思路】
(1)設計返回資訊
- 當前節點的最大距離:這正是我們需要求的
- 當前節點的最大深度:這個值用於輔助求最大距離
(2)遞迴邊界條件:即最小情況時的返回資訊
當node=null時,當前節點最大距離即為0,深度也為0
(3)每一次遞迴向上傳遞資訊的各種可能性
-
當前節點的最大距離取值為如下三種可能性:
-
左子樹的最大距離
如上圖中,1的左子樹最大距離就是紅色線6-2-9那根
-
右子樹的最大距離
-
包含當前節點的橫跨左右兩子樹深度的距離
如上圖中的綠色線。
其求法為:
左子樹的深度 + 1 + 右子樹的深度
-
-
當前節點的高度值存在兩種可能性:
- 左子樹更高,則為左子樹高度+1
- 右子樹更高,則為右子樹高度+1
程式碼:
/**
* 求二元樹的最大距離
*/
class FindMaxDistance{
public static class ReturnData{
public int maxDistance;
public int h;
public ReturnData(int maxDistance , int n){
this.maxDistance = maxDistance;
this.h = h;
}
}
public static int getMaxDistance(TreeNode head){
return process(head).maxDistance;
}
public static ReturnData process(TreeNode head){
if(head == null)
return new ReturnData(0,0);
ReturnData leftData = process(head.left);
ReturnData rightData = process(head.right);
int crossHeadDistance = leftData.maxDistance + 1 + rightData.maxDistance;
/* 當前maxDiatance就是上面談到的三種可能性中選擇最大的,然後作為返回資訊的maxDistance */
int curMaxDistance = Math.max(Math.max(leftData.maxDistance,rightData.maxDistance),crossHeadDistance);
/* 同理當前H也一樣*/
int curH = Math.max(leftData.h,rightData.h) + 1;
return new ReturnData(curMaxDistance, curH);
}
}
4.最大的快樂指數♂
N個員工,編號為1~N
他們之間有從屬關係,也就是說他們的關係就像一棵以校長為根的樹,父結點就是子結點的直屬上司。現在有個宴會,宴會每邀請來一個員工 i 都會增加一定的快樂指數 Ri,但如果某個員工的直屬上司來了,那麼這個員工就不會來。計算邀請哪些員工可以使快樂指數最大,輸出最大的快樂指數
【思路】
根據題意,首先設計出結點類:
public static class Node{
public int huo;
public List<Node> nexts;
public Node(int huo){
this.huo = huo;
nexts = new ArrayList<>();
}
對於每一個結點X(假設他的孩子為x1,x2…xn),只有來和不來情況,下面對這兩種可能性分別討論:
-
X來。
此時以X為根的樹的活躍度為所有孩子不來時的活躍度和 :
x1不來的活躍度 + x2不來的活躍度 + ... + xn不來的活躍度 -
X不來
此時以X為根的樹的活躍度為所有孩子來或者不來時的活躍度和 :
max(x1來的活躍度, x1不來的活躍度) + max(x2來的活躍度, x2不來的活躍度) + ... + max(xn來的活躍度,xn不來的活躍度)
啊,好像DP~~
對這就是樹形DP。
那麼現在我們來設計返回類ReturnData
返回類包含兩個資訊:當前節點來的活躍度、當前節點不來的活躍度
public static class ReturnData{
public int lai_huo;
public int bu_lai_huo;
public ReturnData(int lai_huo , int bu_lai_huo){
this.lai_huo = lai_huo;
this.bu_lai_huo = bu_lai_huo;
}
}
完整程式碼如下:
class MaxHappy{
public static class Node{
public int huo;
public List<Node> nexts;
public Node(int huo){
this.huo = huo;
nexts = new ArrayList<>();
}
public static class ReturnData{
public int lai_huo;
public int bu_lai_huo;
public ReturnData(int lai_huo , int bu_lai_huo){
this.lai_huo = lai_huo;
this.bu_lai_huo = bu_lai_huo;
}
}
/* 主函數呼叫入口 */
public static int getMaxHappy(Node head){
return Math.max(process(head).lai_huo , process(head).bu_lai_huo) ;
}
public static ReturnData process(Node head){
int lai_huo = 0 , bu_lai_huo = 0;
for(int i = 0 ; i < head.nexts.size() ; i ++ ){
Node next = head.nexts.get(i);
ReturnData nextData = process(next);
/* 當前節點來的情況 */
lai_huo += nextData.bu_lai_huo;
/* 當前節點不來的情況 */
bu_lai_huo += Math.max(nextData.lai_huo , nextData.bu_lai_huo);
}
return new ReturnData(lai_huo , bu_lai_huo);
}
}
}
小結
其實之前在做此類題時,採用遞迴方法會在遞迴中幹許多事情,或者還會設定全域性變數、中間值啥的。而該方法比較清晰地將每次遞迴需要做什麼事情,傳遞什麼資訊打包。在每次呼叫時可以只用關注傳遞資訊中的每個值得所有可能性。
另外,進一步理解遞迴設計、應用或者對遞迴過程有所疑惑的小夥伴可瀏覽之前的文章:
- [演算法系列] 搞懂遞迴, 看這篇就夠了 !! 遞迴設計思路 + 經典例題層層遞進
- [演算法系列] 遞迴應用: 快速排序+歸併排序演演算法及其核心思想與拓展 … 附贈 堆排序演演算法
- [演算法系列] 深入遞迴本質+經典例題解析——如何逐步生成, 以此類推,步步為營
- [演算法系列]搞懂DFS(1)——經典例題(數獨遊戲, 部分和, 水窪數目)圖文詳解
- [演算法系列]搞懂DFS(2)——模式套路+經典例題詳解(n皇后問題,素數環問題)
- [演算法系列]遞迴應用——二元樹(1):二元樹遍歷詳解解+LeetCode經典題目+模板總結
待續。。。