【資料結構基礎】線性資料結構——三種連結串列的總結及封裝(C和Java)
前言
資料結構,一門資料處理的藝術,精巧的結構在一個又一個演演算法下發揮著他們無與倫比的高效和精密之美,在為資訊科技打下堅實地基的同時,也令無數開發者和探索者為之著迷。
也因如此,它作為博主大二上學期最重要的必修課出現了。由於大家對於上學期C++系列博文的支援,我打算將這門課的筆記也寫作系列博文,既用於整理、消化,也用於同各位交流、展示資料結構的美。
此係列文章,將會分成兩條主線,一條「資料結構基礎」,一條「資料結構拓展」。「資料結構基礎」主要以記錄課上內容為主,「拓展」則是以課上內容為基礎的更加高深的資料結構或相關應用知識。
歡迎關注博主,一起交流、學習、進步,往期的文章將會放在文末。
這一節我們將開始總結一個常見的資料結構:線性表。
由於線性表的內容較多,本節只能總結部分內容。
主要為兩種基礎的線性表,陣列和連結串列。在簡單介紹其定義之後,重點會放在實現對其各種操作的簡單實現及封裝。
本節思維導圖如下:
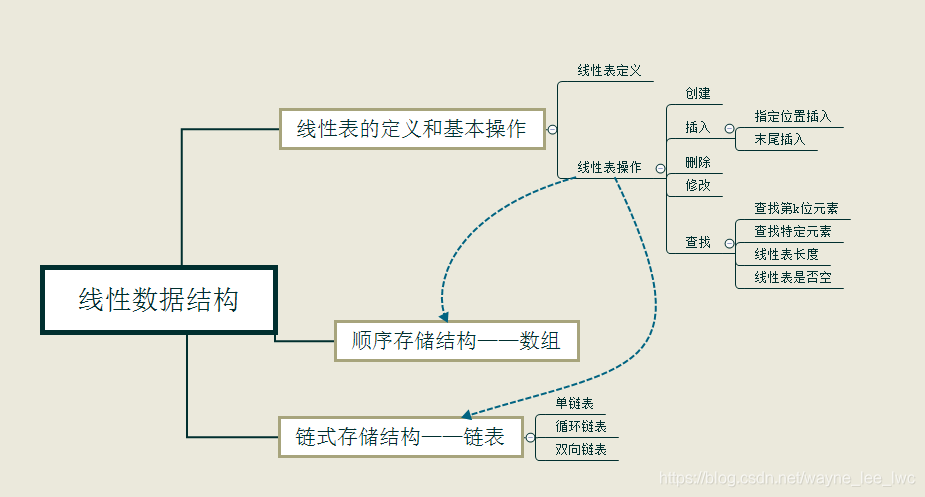
鏈式儲存結構——連結串列
連結串列也是一種線性表,相較於陣列不同的是,連結串列中的元素的儲存結構是連結式的。
作為一種線性表,元素在邏輯上是連續的,有順序且呈線性排列;但在儲存上他們並不像順序表一般佔據連續的空間,而是隨機分佈在空間各處,每個結點通過指標來記錄後繼的地址形成連結。
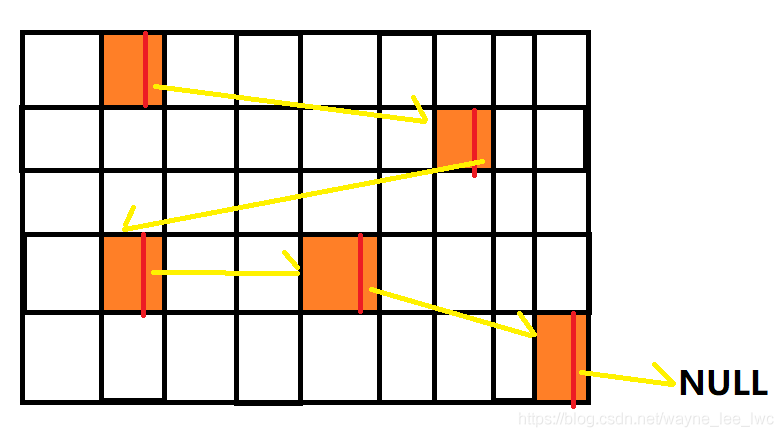
從上面例子中也可看出,每個結點在其所佔的空間中除了要儲存本身的資料外,還需要單獨使用一片空間儲存其後繼的指標。
所以一個結點可以大致表示成如下形式:

他們連結起來可以表示成:
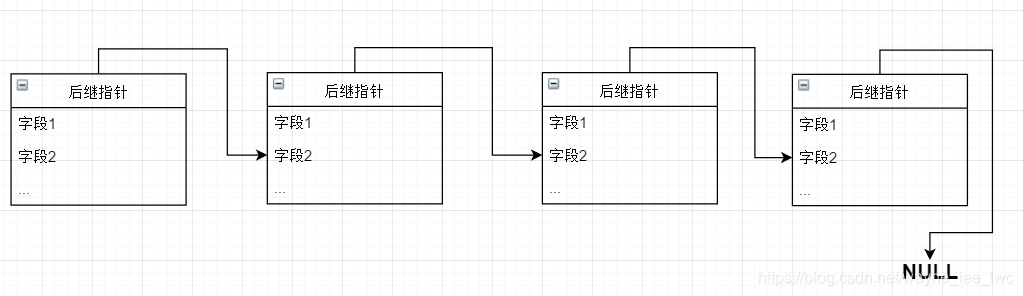
可以注意到,連結串列的尾結點沒有後繼,所以其後繼指標需要指向空。且由於連結串列的內容是隨機分佈在空間中的各處。所以為了便於存取他們,我們需要保留頭結點的指標,也就是知道頭結點的位置,對於後面的元素便可以通過後繼節點依次存取到他們。
連結串列的優點在於其空間上的靈活,連結式的儲存似的其長度可以任意改變,不像陣列的長度是定值。缺點就在於其失去了順序表中靜態存取結點的能力,不能直接按照下標存取某元素,使得存取給定下標的元素必須遍歷連結串列。
單連結串列的實現
知道了連結串列的設計方案,下面我們就來將設計方案付諸實踐,變成程式碼。
實際上正如上文所說,連結串列的內容相較於一般的節點來說只是多出了後繼指標,所以我們完全可以在一般的資料結點的基礎上加上後繼指標來得到連結串列元素。
單連結串列元素
//C
typedef struct _Node{
int value;
struct _Node * next;
}Node;
Node * head;
//Java
class Node{
int value;
Node next;
}
Node head;
單連結串列的遍歷
遍歷整個單連結串列,必不可少的條件就是獲得頭指標。有了頭指標就可以根據後繼指標依次存取後面的元素。
那麼什麼時候連結串列遍歷結束呢?通過上文的例子不難發現,連結串列的尾結點的後繼指標為空,所以可以根據是否為空來判斷這一結點是否是有效結點,這樣既可以在遍歷過尾結點後準確而迅速的結束遍歷,也可以應對連結串列為空的情況(頭指標為空)
下面以遍歷連結串列獲得所有元素加和為例:
//C
int getSum(Node * head){
int sum = 0;
while(head){
sum += head->value;
head = head->next;
}
return sum;
}
//java
class LinkedList{
Node head;
public int getSum(){
int sum = 0;
Node cur = head;//不能直接使用頭參照進行遍歷
while(cur != null){
sum += cur.value;
cur = cur.next;
}
return sum;
}
}
複雜度:O(n)
插入元素
向連結串列的優秀之處在於其資料組織是動態的,插入一個元素可以不需要像陣列一樣將後面的元素向後移動。可以通過對後繼指標的操作來完成插入。
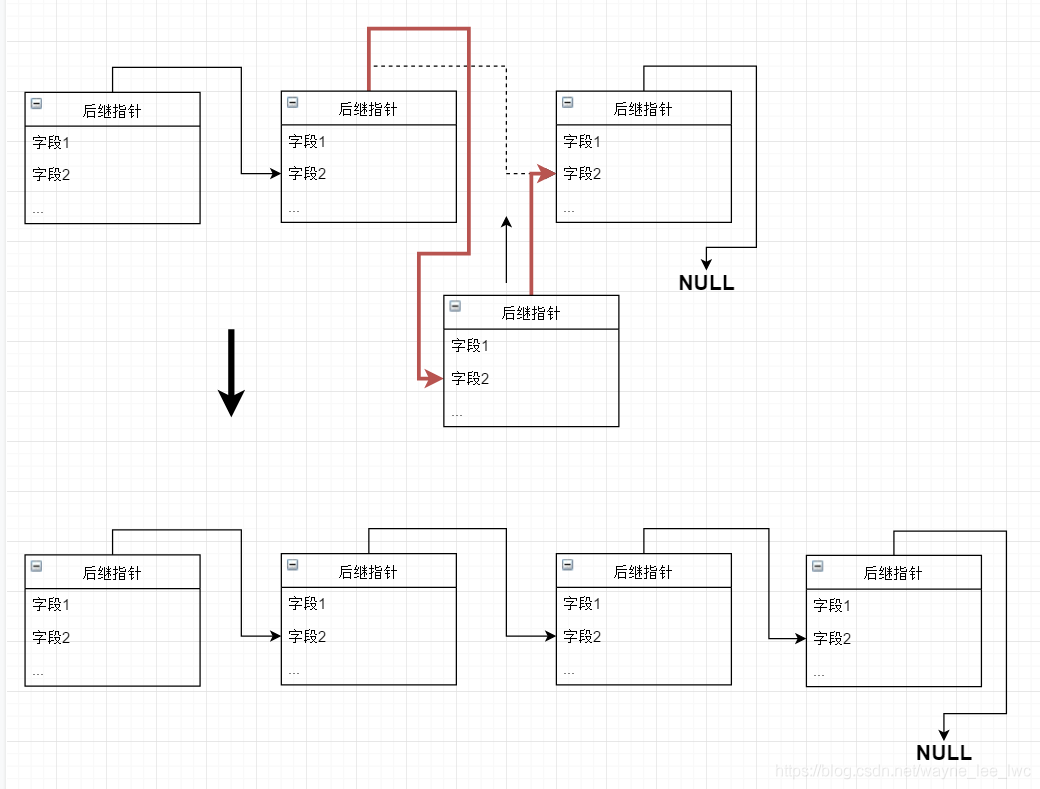
以將元素node插入下標為index(0 ≤ index ≤ len)的位置為例,該函數需要返回操作後的頭指標:
//C
Node * insert(Node * head,Node * node,int index){
int curIdx = 0;
if(index == 0){//新元素位於隊首
node->next = head;
return node;
}
while(head){
if(curIdx = index - 1 || head->next = NULL){
node->next = head->next;
head->next = node;
break;
}
head = head->next;
curIdx++;
}
return head;
}
//Java
class LinkedList{
Node head;
public Node insert(Node node,int index){
if(index == 0){//插入頭
node.next = head;
head = node;
}
int curIdx = 0;
Node cur = head;
while(cur != null){
if(curIdx = index - 1 || cur.next == null){
node.next = cur.next;
cur.next = node;
break;
}
cur = cur.next;
curIdx++;
}
return head;
}
}
上面的程式可以完成將指定元素插入到指定下標的操作。
需要注意的是,該程式特殊規定對於下標超出當前連結串列規模時會預設插入隊尾。
由於連結串列不能直接靜態的找到某下標的位置,所以遍歷尋找到該下標的位置還是不可避免的開銷,主要的複雜度就產生在這裡。
複雜度:O(n)
哨位結點
注意到上面的插入操作中如果將元素插入隊首,那麼頭指標需要更新成為新元素。那麼為了避免頻繁的更改頭指標,我們可以引入哨位結點來解決這個問題。
哨位結點又稱哨兵結點,它是一個空節點,沒有實際意義,是人為規定的預設隊首。真正的隊首一定是哨兵節點的後繼節點,這樣一來,插入元素至隊首就變成了插入元素到哨兵節點後面。此時可以保證不論如何頭指標不會更改。
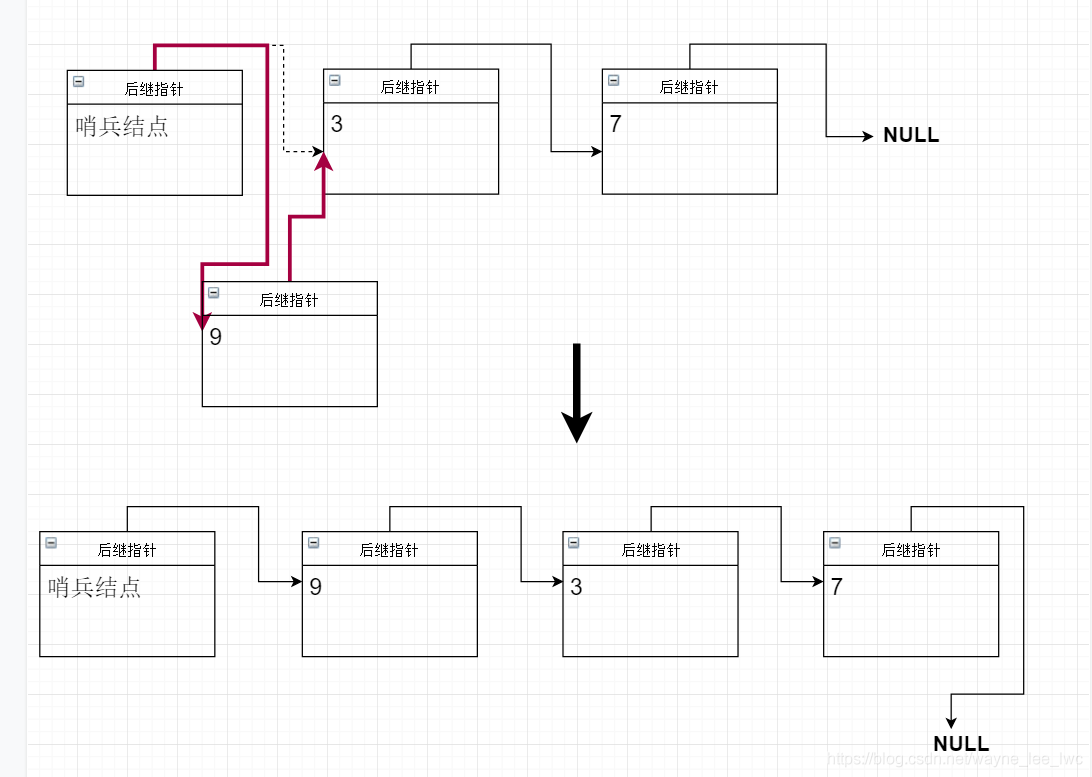
使用哨位節點,我們可以重新實現插入操作,此時頭指標不會發生改變。
//C
int insert(Node * head,Node node,int index){
int curIdx = 0;
while(head){
if(curIdx == index || head->next == NULL){
node->next = head->next;
head->next = node;
break;
}
head = head->next;
curIdx++;
}
return 1;
}
//Java
class LinkedList{
Node head;
public boolean insert(Node node,int index){
int curIdx = 0;
Node cur = head;
while(cur != null){
if(curIdx = index || cur.next == null){
node.next = cur.next;
cur.next = node;
break;
}
cur = cur.next;
curIdx++;
}
return true;
}
}
統一了插入隊首和插入隊中,美感增加了呢。
複雜度:O(n)
單連結串列的不足
單連結串列存在一個問題,其中的元素的只能單向存取不能逆序遍歷。也就是說,我們僅知道一個節點的後繼節點卻不知道其前驅結點。
為了解決這個問題,我們需要引入迴圈連結串列和雙向連結串列。
迴圈連結串列
迴圈連結串列指的是將一個單連結串列首尾相接,使尾結點的後繼為頭結點,使頭結點的前驅為尾結點。
在迴圈連結串列中,為了方便對空連結串列的處理,最好要保留哨位結點。
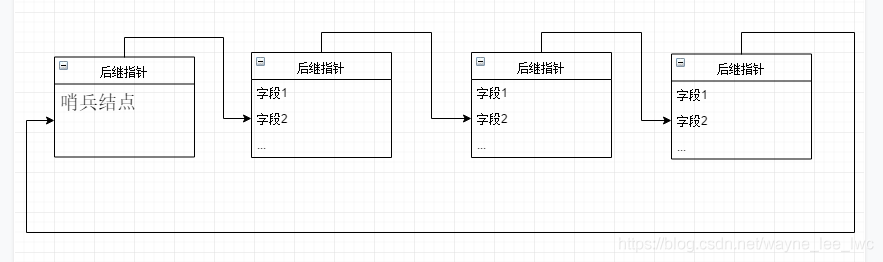
因此,對於空連結串列,就是僅有哨位結點作為「頭結點」,其後繼指向它自身:
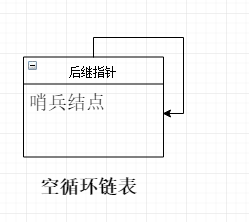
這也提示了我們如何建立並初始化一個迴圈連結串列:就是初始化一個哨位結點,並使它的後繼指標指向自己:
建立/初始化迴圈連結串列
通過上面的敘述不難發現,迴圈連結串列僅是改變了尾結點的指標,並沒有改變結點本身的結構。所以我們可以沿用單連結串列的結點定義。
//c
Node * createCircularList(){
Node * head = (Node *)malloc(sizeof(Node));
head->next = head;
return head;
}
//java
public class CircularList {
class Node{
int value;
Node next;
}
Node head;
public CircularList() {
head = new Node();
head.next = head;
}
}
迴圈連結串列尋找前驅
下面我們就來使用迴圈連結串列來尋找一個元素的前驅。
思路非常的簡單,就是不斷的向後遍歷,直到尋找到一個元素的後繼等於詢問元素即可。
//c
Node * getPrecursor(Node * curr){
Node * node = curr;
while(node->next != curr){
node = node->next;
}
return node;
}
//java
public class CircularList {
class Node{
int value;
Node next;
}
Node head;
public Node getPrecursor(Node curr) {
Node node = curr;
while(node.next != curr) {
node = node.next;
}
return node;
}
}
複雜度:O(n)
對於常規的增刪改查操作,迴圈連結串列的操作基本上同單向連結串列沒有本質上的區別。
一個需要注意的地方就是迴圈連結串列的遍歷,由於迴圈連結串列的尾結點的後繼是頭結點,所以在判斷遍歷結束時條件需要更改為後繼節點是否為頭結點。其餘操作這裡就不再一一贅述了。
雙向連結串列
雙向連結串列是在單連結串列的基礎上修改結點結構得到的,在一個結點上不僅記錄該節點的後繼還記錄該節點的前驅,從而在結點之間形成雙向連線。
一個結點可以表示成這樣:
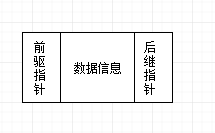
這樣就需要我們對資料結點的結構進行修改:
//C
typedef struct _DoublyNode{
int value;
DoublyNode * prev;
DoublyNode * next;
}DoublyNode;
//java
public class DoublyList {
class Node{
int value;
Node prev;
Node next;
}
private Node head;
}
依據這樣的結構,他們連線起來可以表示成:
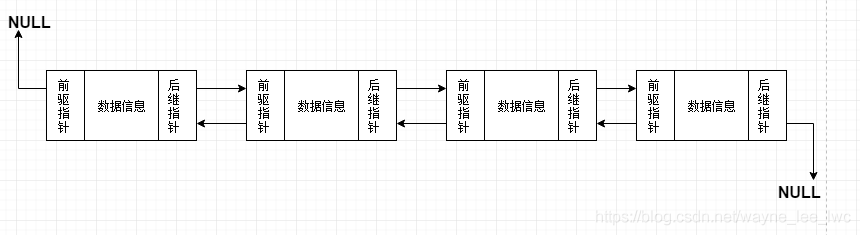
當然我們也可以給他們加上哨位結點並且使用環形結構:

雙向連結串列的操作相較於單連結串列會複雜不少,這裡我們重新來封裝一下基於雙連結串列的增刪查。由於雙向連結串列需要同時維護前驅和後繼指標,所以為了便於插入和刪除,我們有必要使用首位兩個哨位結點來控制。
初始化雙向連結串列
那麼初始化或者建立一個雙向連結串列的工作就不同於單向連結串列了,需要初始化兩個哨位結點,並且將它們相連。
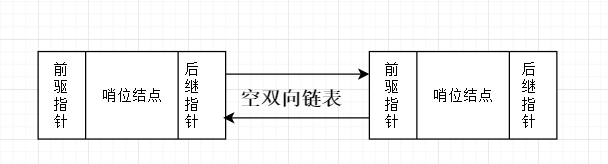
//c
DoublyNode * createDoublyList(){
DoublyNode * head = (DoublyNode *)malloc(sizeof(DoublyNode));
DoublyNode * tail = (DoublyNode *)malloc(sizeof(DoublyNode));
head->next = tail;
head->prev = NULL;
tail->next = NULL;
tail->prev = head;
return head;
}
//java
public class DoublyList{
private Node head;
private Node tail;
public DoublyList(){
head = new Node();
tail = new Node();
head.next = tail;
head.prev = null;
tail.next = null;
tail.prev = head;
}
}
插入元素
向連結串列中插入一個元素,需要斷開原有的連結,重建兩次連結。
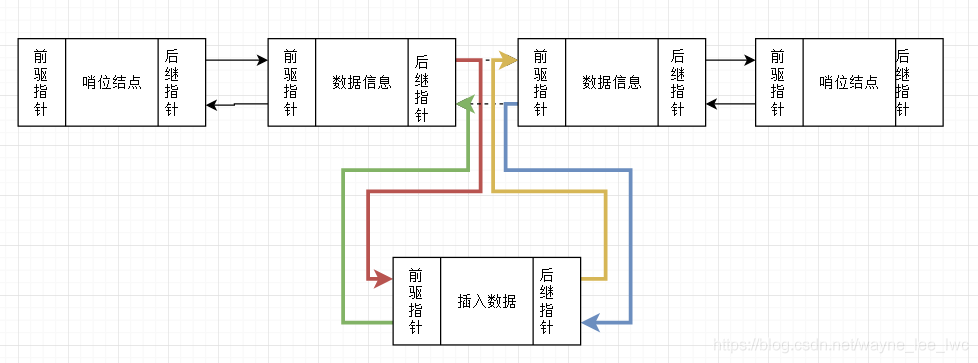
重建連結的過程會有一些繞,因為它涉及到後繼元素的前驅指標,這需要巢狀兩次,並且更改前驅和後繼節點的順序也有可能造成bug。
//C
int insert(DoublyNode * node,DoublyNode * head,int index){
if(index < 0 || node == NULL)
return 0;
int curr = 0;
while(head->next){
if(curr == index || head->next->next == null){
head->next->prev = node;
node->next = head->next;
node->prev = head;
head->next = node;
break;
}
curr++;
head = head->next;
}
return 1;
}
//java
public class DoublyList{
private Node head;
public boolean insert(int index,Node node){
if(index < 0 || node == null)
return false;
Node head = this.head;
while(head.next != null){
if(curr == index || head.next.next != null){
head.next.prev = node;
node.next = head.next;
node.prev = head;
head.next = node;
break;
}
curr++;
head = head.next;
}
}
return true;
}
查詢元素前驅
用雙向連結串列獲得前驅真的是最簡單的事情了,因為前驅就在結點中儲存著,直接返回就好。
//c
DoublyNode * getPrecursor(DoublyNode * node){
if(node)
return node->prev;
return NULL;
}
複雜度:O(1)
快速的時間複雜度來源於雙向連結串列在空間複雜度上面的妥協。可以說雙向連結串列的取錢去操作是空間換時間的典範
刪除元素
刪除元素,需要重建兩條邊並且刪除結點。難點在於釋放元素的時機,和修改前驅結點的後繼以及修改後繼結點的前驅。
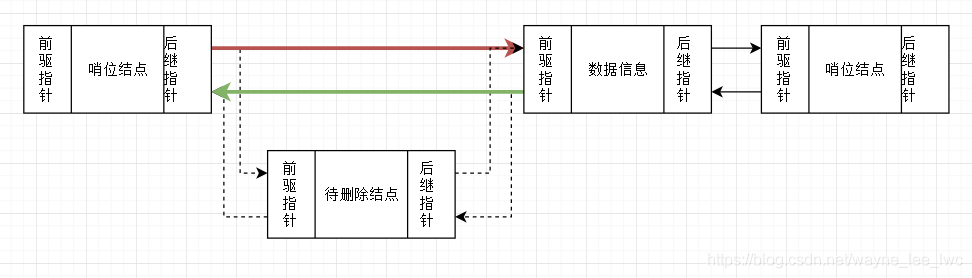
//c
int delete(DoublyNode * head,int index){
if(index < 0)
return 0;
int curr = 0;
head = head->next;//先向後跳一格,檢視當前元素是否是待刪除元素
while(head->next){
if(curr == index){
head->prev->next = head->next;
head->next->prev = head->prev;
free(head);
return 1;
}
}
return 0;
}
//java
public class DoublyList{
private Node head;
private Node tail;
public boolean delete(int index){
if(index < 0)
return false;
int curr = 0;
Node head = this.head;
head = head.next;//先向後跳一格,檢視當前元素是否是待刪除元素
while(head.next != null){
if(curr == index){
head.prev.next = head.next;
head.next.prev = head.prev;
return true;
}
}
return false;
}
}
三種連結串列的簡單總結
上面簡單介紹了三種連結串列的定義及各種操作以及連結串列中的哨位結點。
有些同學可能會納悶他們能否組合使用,還是說像是隻有單連結串列才能組織成迴圈連結串列的形式這種限制。
博主認為:連結串列迴圈、哨位結點乃至雙向連結串列是連結串列結構的不同設計思想,並不專屬於某種設計。我們可以看到哨位結點在單向、迴圈連結串列中的使用,也可以看到雙向的迴圈連結串列。所有的結構都是為演演算法或功能服務的,為了配合他們完成任務,可以使用各種合適的設計方案。
往期部落格
參考資料:
- 《資料結構》(劉大有,楊博等編著)
- 《演演算法導論》(托馬斯·科爾曼等編著)
- 《圖解資料結構——使用Java》(胡昭民著)