影象如函數

影象分類

完美影象

完美影象（perfect image）是連續圖形，完美影象由一個物理過程所產生。

將這個物理過程用I所表示，他們代表了從平面上的點到一個數位的對映，即

$I:R^2\to R$

Remark: $0<I(\cdot )<\infty$

Remark: 抽象後我們可以將定義域看作超平面上的點，其維度可以超過2 。如此，哦我們可以將它們定義成一個對映：

$I:R^k\to R$

由所經受的物理過程所決定

Remark: 完美影象僅在無法取樣的時候存在抽象化。

例子：朗伯模型（Lambertian Image）

朗伯模型是一個經典的漫反射模型。朗博模型中光的反射量由入射角的餘弦角所決定。

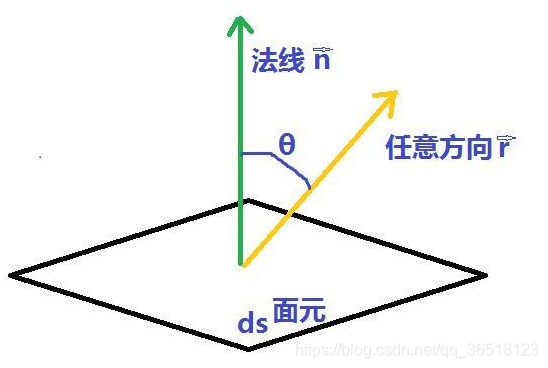
考慮一個點$x\in R^3$ 在朗伯表面上，其對此表面的法向量$n(x)$ 。入射角的方向是$l(x)$。 此時反射可以寫作：

$R(x)=\rho l(x{)}^{T}n(x)$

其中$\rho$是一個常數，用於描述材料屬性。

仍和的反射光與我們的影象平面相交時，都會引起我們的完美影象

$I(u)=P(R(x))$

其中P投影函數，I(u)是投影的能量

問題：朗伯模型的缺點是什麼？

朗伯模型難以對光滑的表面，比如金屬，進行建模。此時我們需要Phong模型。

數位影像

雖然我們不能直接獲得完美影象，但是我們可以通過電子裝置將其轉換之。如此做，我們可以通過量化和取樣完美影象來獲得數位影像。

定義：數位影像是取樣和量化完美影象所獲得。它們展現出從點到非負自然畫素（non-negative natural pixels)到自然數的對映

$N_0^2\to N_0$

Remark：數位化是一個投影($R^2\to R$)

Remark：「取樣」指的是座標值的數位化，「量化」指的是（能量，亮度）強度值的數位化。

Remark：取樣密度由感測器的物理限制所約束

Remark：量化深度由特殊的硬體所決定。8bit的量化廣泛應用於數位化的影象。

Remark： 在特定的數位化情境下（可能指Bayer pattern）完美影象被用於梳理感興趣的訊號。

數位影像建模

對數位影像的數學解釋

1. 一個從畫素到數位的離散函數
2. 作為對於原來完美影象的一個近似，我們對一個函數的值域和定義域進行了一個泛化，並且用函數的形式呈現出來。（We generalize domain and range of this function to once again consider a continuous image, albeit an approximate one to our original perfect image，這句話有點離譜）

定義：一個離散影象是一個數位影像的自然數的數位型概述。它獲取數位影像中的整數畫素位置並且將其對映到整數畫素值上。$I:Z^3\to Z$

Remark：它可以表示更高維的影象，比如$Z^3$（視訊），並且值域維度也可以更高，比如$Z^3$（三色影象）。

Remark：我們將一個影象的值於的整數的子集稱作$\Lambda$

例子：Potts 模型

Potts模型是一個離散影象模型。Potts模型最初在統機物理學中作為雙態化模型（two-state Ising model）的推廣而派生出來的。它假定了一個分段常熟影象訊號。對於大小為$n\times n$的影象，我們將其寫作能量泛函（energy functional）。

$E(I)=\beta {\Sigma }_{s=1}^{n-1}{\Sigma }_{t=1}^n(1[I(s,t)\ne (s+1,t)]+\beta {\Sigma }_{s=1}^{n-1}{\Sigma }_{t=1}^n(1[I(s,t)\ne (s,t+1)])$

$\beta$是一個建模常數，最初與所研究的材料的物理性質有關，我們忽略了區域上的邊界條件$1$是指示器函數。根據Potts模型的定義，我們發現模型的能量正比於橫縱畫素的變化。當影象$I$由大的恆定取與，他將具有相應的能量。

定義：一個連續影象可以將離散影象泛化（generalize）為定義域與值域。

Remark：對於離散影象的相似的定義域和值於的泛化可以用於連續模型

Remark：離散與連續混合的表現是非常常見的

Remark：插值。通過數位化過程，最初的完美影象已經被量化到整數座標了。為了研究連續圖形並分析，我們需要不斷地對非整數座標進行插值。

影象操作

在影象的函數解釋下，我們可以用數學的角度去處理影象。

在影象的函數解釋下，影象的三個主要操作：

1. 空間範圍操作（Spatial Range Operation）如計算影象所有強度值的和
2. 範圍對映操作（Range map operation）比如計算圖的差別
3. 定義域操作或幾何變換比如平移和旋轉

空間範圍操作

空間範圍操作講一個區域內所有資訊集合起來，將一個影象的區域定義成$W\subseteq \Lambda \subseteq Z^2$ 。其中W代表一張影象中的視窗（windows）。

定義：一個空間範圍操作$f$是一個講一張圖對映到一個實數的函數

$f:W\times (Z^2\to Z)\to R/W\times I\to R$

其中$I$為影象本身。

Remark：我們使用縮寫$I[W]$來表示定義域由$W$所擷取的新圖，這種新圖也叫子圖（sub-image），或者image patch。

Remark：我們可以講$W$當作一種函數，當$W=\Lambda \to B^{\Lambda }$時，這種函數講畫素對映到 B = { 0 , 1 } B=\{0, 1\} B={0,1}。我們可以將mask應用在影象上。在空間範圍操作應用之前，我們也可以基於視窗$W$在函數$f$上實現特殊的定義域。

Remark：一個空間範圍操作是線性的當

$f_W({\alpha }_i{I}_i+{\alpha }_j{I}_j)={\alpha }_i{f}_W(I_i)+{\alpha }_j{f}_W(I_j)$

${\alpha }_i$與${\alpha }_j$是任意常標量。

Remark：空間範圍操作可以在影象領域中被組合去組成複雜的操作符。

範圍對映操作

範圍對映擦歐總作用於影象值域，他們將單個操作作用域整個影象域$\Lambda$

定義：一個範圍對映操作$g:(W\times I\to R)\times I\to J$對於影象$J$來說，是一個函數$f$作用域影象定義域$\Lambda$的每一個空間中，範圍對映操作會產生一個新的影象。

影象$J$ $f:W\times I\to R$

procedure GENERIC_RANGE_MAP_OPERATOR:
foreach pixel s $\in {\Lambda }_J$ do

​ let $W_s$ be the window into $\Lambda$ at centered at s

​ $J(s)=f(I,W_s)$

​ end for

end procedure

Remark：範圍對映操作的輸出集是實數集。實際操作上，它常被放寬到實數或者其他的範圍。

Remark：範圍對映操作通常被用於一個被稱作強度轉換（intensity transformations）的畫素視窗。文獻中存在許多可能的強度變換 (very many possibly intensity transformations exist in the literature，不會翻譯)並且包括了操作符比如直方圖均衡化（histogram equalization），線性放大（linear scaling）或者log轉換等。

例子單畫素範圍對映強度轉換。一個強度轉換的例子是對負影象的轉換。每一個新畫素的值是輸入值的負值。

$J(S)=-I(S)$

Remark：一個特殊的範圍對映例子是對映到二進位制畫素而不是實數：

$g:(W\times I\to B)\times I\to B$

對於二進位制影象$B$。

例子二進位制函數的範圍對映

考研率一個二進位制閾值操作符$f_b$。在一個確定的範圍對每一個畫素視窗，$f_b$選擇畫素值$({\Gamma }^{-}\le I[W]\le {\Gamma }^{+})$。

$$f_b(I[W];{\Gamma }^{-},{\Gamma }^{+})=\{\begin{array}{rl}1& {\Gamma }^{-}\le I[W]\le {\Gamma }^{+}\\ 0& otherwise\end{array}$$

或在更大的視窗中使用空間範圍操作符，比如：

$$f_b(I，W;{\Gamma }^{-},{\Gamma }^{+})=\{\begin{array}{rl}1& {\Gamma }^{-}\le sum(I,W)\le {\Gamma }^{+}\\ 0& otherwise\end{array}$$

Remark：在一個範圍操作符中，空間範圍操作在一個大視窗$W$將應用相同的操作在這個圖的每一個區域內。

Remark：一個特別重要的引數在一個空間操作符中的是核（kernel）。一個核$\kappa$是一個與$W$大小相同的矩陣。核的值都是實數，$\kappa \in {\mathbb{R}}^{|W|}$。在核操作中，核$\kappa$與影象視窗$I[W]$的元素積操作被計算與累加起來。這個操作最容易被向量化的核$\kappa$與影象視窗$I[W]$的點積所表示。向量化一個矩陣代表連線一個矩陣的所在列，並且將其連成一個長列向量。

當核操作被應用於整個影象中的一個範圍對映的時候，我們可以將這個過程稱作離散折積，並用符號$\otimes$表示。我們為了輸出影象位置$J(s,t)$而寫下這個折積。核的大小是$2m+1\times 2m+1$因此一個視窗可以索引至$s-m...s+m$與$t-n...t+n$被寫作

$$J(s,t)=\kappa \otimes I[W]={\Sigma }_{k=-m}^m{\Sigma }_{l=-n}^n\kappa (k,l)I(s-k,t-l)={\vec{\kappa }}^{T}I\overrightarrow{[W]}$$

我們將核對映應用於所有位置，適當地考慮影象邊界，即簡單的說$\kappa \otimes I$，它是建立影象的函數。這裡有一個折積的連續模擬，但是我們暫不進行討論。假如維度與核相匹配，這個操作可以清晰地泛化到高維。

例子離散影象求導

在影象的函數解釋下，像這樣的計算式非常正常的。

對$I(x,y)$的部分求導是

$$\frac{\partial I(x,y)}{\partial x}=li{m}_{h\to 0}\frac{I(x+h,y)-I(x,y)}{h}$$

考慮一個離散影象模型，我們有一個固定的值$h$可以讓我們去考慮一個有限（離散）差別的解釋：

$$\frac{dI(x,y)}{dx}=\frac{I(x+h,y)-I(x,y)}{h}$$

最後，考慮到離散影象$I$，我們可以將$h$設為1來表示一個畫素的差別。我們將有限差別符設為${\nabla }_x=\frac{dI(x,y)}{dx}=I(x+1,y)-I(x,y)$

將其用於核中，則縱向為$\kappa =[1,-1{]}^T$，橫向為$\kappa =[1,-1]$

Remark：範圍操作可以是二元，三元，或者同時任意數位

例子影象拉普拉斯與0-crossing

考慮影象$I$ 被核${\kappa }_1$與${\kappa }_2$所折積處理，${\kappa }_1$與${\kappa }_2$是分別從$\sigma =1$與$\sigma =2$的高斯函數中取樣出來。將折積出來的影象稱為$G_1$與$G_2$。取兩者之差$G_2-G_1$。可以發現影象的邊緣被凸顯出來。

一個突然的強度改變會在一階導提升到頂峰，或者在二階導達到0-crossing

之前的例子（離散影象求導）表現了一階導，這個例子考慮二階導

$${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$$

這兩個（二階導和高斯核）效果相近

專業術語翻譯對照（不確定是不是對的）

完美影象: perfect Image

定義域: Domain

值域：range

朗伯模型Lambertian Model

數位影像 digital Image

非負自然畫素 non-negative natural pixels

取樣：Sampling

量化：quantization

感興趣的訊號 signals of interest.

雙態化模型：two-state Ising model

指示器函數：indicator function

泛化generalize

空間範圍操作 Spatial Range Operation

範圍對映操作 Range map operation

文獻中 in the literature