【密碼學原理】分組密碼，Feistel結構實現

現在使用的大多數對稱分組加密演演算法都是基於Feistel分組密碼結構的，所以研究Feistel密碼的設計原理很重要。先看串流加密法和分組密碼的不同，然後看Fristel結構在分組密碼上的應用。

	金鑰	形式	範例
串流加密法	隨機（可一次一密） 金鑰流必須提前由安全通道傳送 共用對稱金鑰	位流	Vienere密碼 Vernam密碼
分組密碼	共用對稱金鑰	分組 等長明密文	DES AES

分組密碼作用在n位明文分組上，產生n位密文分組。共有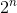個不同的明文分組，由於加密是可逆的，所以每個明文分組將唯一對應一個密文分組。這樣的變換稱為可逆變換，或者非奇異變換。在可逆變換中，不同的變換將有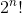個。

代替和置換

代替：每個明文元素或元素組被唯一的替換為相應的密文元素或者元素組。

代替中需要有代替表，將每個元素的代替元素唯一的表示記錄。

置換：明文元素的序列被替換為該序列的一個置換。就是說，序列中沒有元素被新增、刪除或者替換，但是序列中元素出現的順序改變了。

在代替中，元素按照一定的規則被替換，替換規則就是代替表，代表表也即是金鑰。

在置換中，沒有元素被替換，但是明文元素的序列被改變，例如用柵欄技術：按照對角線的順序寫明文，按行的順序讀作密文。這種技術很容易被破譯，更為複雜的方案即用矩陣的方式：按行寫明文，按列讀作密文，讀密文之前將列的次序打亂，列的次序變換就是演演算法的金鑰。

單純的置換密碼有著與明文相同的字母頻率特徵，容易被識別。多次置換密碼相對來說要安全很多。

混淆和擴散

擴散：儘可能的使明文和密文之間的統計關係變得複雜，防止推匯出金鑰。使明文的統計特徵消散在密文中，讓每個密文數位被多個明文數位影響。

混淆：儘可能使密文和加密金鑰之間的統計關係更加複雜，防止攻擊者發現金鑰。

Feistel結構

Feistel結構的具體實現依賴以下幾個引數和特徵：

• 分組長度：分組越長意味著安全性越高，但會降低加解密的速度。
• 金鑰長度：金鑰長度越長意味著安全性越高，但會降低加解密的速度。
• 迭代次數：Feistel密碼的本質在於單輪不能提供足夠的安全性，多倫加密可以取得很高的安全性。典型的迭代16輪。
• 子金鑰產生演演算法：子金鑰產生越複雜，密碼分析越困難。
• 輪函數F：輪函數越複雜，抗攻擊能力越強。